 |
17.Теоремы существования эйлеровых и гамильтоновых циклов.
|
|
|
|
17. Теоремы существования эйлеровых и гамильтоновых циклов.
Эйлеровым путем в графе называется путь, содержащий все ребра графа.
Эйлеровым называется цикл, проходящий по каждому ребру графа ровно один раз. Граф, имеющий эйлеров цикл, тоже будем называть эйлеровым.
Теорема: Пусть G – конечный граф. Этот граф является эйлеровым тогда и только тогда, когда:
1)Граф является связным
2)все степени его вершин четные
Док-во:
Пусть P – цепь графа G и выполняются условия 1, 2. Берем одну вершину цепи V. Из условий 1, 2 следует что мы обязательно вернемся в вершину V.
Если цикл прошел не через все ребра, то находим 
(дополнение) в графе G. И в этом дополнении рассматриваем другую цепь Q. Для неё рассуждения аналогичны. Объединим циклы P и Q => объединим и процесс получения, пока не получим эйлеров цикл.
Теорема( обратная без док-ва ): Если граф обладает эйлеровым циклом, то он является связным, а все его вершины — четными.
Гамильтонов путь (или гамильтонова цепь) — путь (цепь), содержащий каждую вершину графа ровно один раз. Гамильтонов путь, начальная и конечная вершины которого совпадают, назвается гамильтоновым циклом.
Теорема: ( О существовании гамильтоновой цепи)
В конечном полном графе, в котором между двумя любыми вершинами имеется некоторый путь имеется гамильтонова цепь.
Док-во: Рассмотрим некоторый путь в графе длины m-1
= [v1, v2, …vm]
Док-ть что исходя из этого пути можно построить гамильтонов путь.
Док-во будем вести от противного: на основании того пути можно построить путь 
=[v1, v2, … vk, , u, vk+1, …. vm] (0 
k m)
Предположим, что такого пути нет.
Т. е. для некоторого k: (u, vk), (u, vk+1)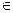 
E(G) – не выполняется.
Тогда (vk, u) 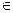E(G) => (u, vk+1) 
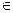E(G) => (vk+1, u) E(G)
|
|
|
Покажем в чем противоречие:
Если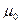 
=[u, v1, v2, …vm] не существует, то (v1, u), …(vm, u) =>
существуют 
=[ v1, v2, …vm, u], вопреки нашему предположению.
18. Задачи о кратчайшем пути.
В практических приложениях имеет большое значение задача о нахождении кратчайшего пути между двумя вершинами связного неориентированного графа. К такой задаче сводятся многие задачи выбора наиболее экономичого (с точки зрения расстояния или времени или стоимости) маршрута на имеющейся карте дорог, многие задачи выбора наиболее экономичного способа перевода динамической системы из одного состояния в другое и т. п. В математике разработан ряд методов для решения подобных задач. Однако весьма часто методы, основанные на использовании графов, оказываются наименее трудоемкими.
Задача о кратчайшем пути на графе в общем виде может быть сформулирована следующим образом. Дан неориентированный граф G=(X, U). Каждому ребру этого графа приписано некоторое число, называемое длиной ребра. В частных случаях это может быть расстоянием между вершинами, соединяемыми ребром и временем или стоимостью проезда по этому ребру и т. п. Требуется для произвольных вершин а и b графа G найти путь, причем такой, чтобы его полная длина была наименьшей.
Рассмотрим Алгоритм Дейкстры:
Дан простой взвешенный граф G без петель и дуг отрицательного веса. Найти кратчайшие пути от некоторой вершины a графа G до всех остальных вершин этого графа.
Пример
 
 
 
 
 
 
 
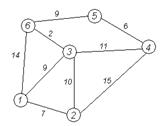
| Рассмотрим выполнение алгоритма на примере графа, показанного на рисунке. Пусть требуется найти расстояния от 1-й вершины до всех остальных.
Кружками обозначены вершины, линиями — пути между ними (ребра графа). В кружках обозначены номера вершин, над ребрами обозначена их «цена» — длина пути. Рядом с каждой вершиной красным обозначена метка — длина кратчайшего пути в эту вершину из вершины 1.
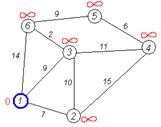
Первый шаг. Рассмотрим шаг алгоритма Дейкстры для нашего примера. Минимальную метку имеет вершина 1. Ее соседями являются вершины 2, 3 и 6.
Первый по очереди сосед вершины 1 — вершина 2, потому что длина пути до нее минимальна. Длина пути в нее через вершину 1 равна кратчайшему расстоянию до вершины 1 + длина ребра, идущего из 1 в 2, то есть 0 + 7 = 7. Это меньше текущей метки вершины 2, поэтому новая метка 2-й вершины равна 7. На графике изначально рассмотрена вершина №3.
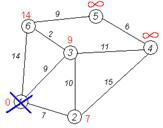
Аналогичную операцию проделываем с двумя другими соседями 1-й вершины — 3-й и 6-й.
Все соседи вершины 1 проверены. Текущее минимальное расстояние до вершины 1 считается окончательным и пересмотру не подлежит (то, что это действительно так, впервые доказал Дейкстра). Вычеркнем её из графа, чтобы отметить, что эта вершина посещена.
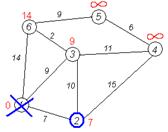
Второй шаг'. Шаг алгоритма повторяется. Снова находим «ближайшую» из непосещенных вершин. Это вершина 2 с меткой 7.
Снова пытаемся уменьшить метки соседей выбранной вершины, пытаясь пройти в них через 2-ю. Соседями вершины 2 являются 1, 3, 4.
Первый (по порядку) сосед вершины 2 — вершина 1. Но она уже посещена, поэтому с 1-й вершиной ничего не делаем.
Следующий сосед вершины 2 — вершина 4/*3*/. Если идти в неё через 2-ю, то длина такого пути будет = кратчайшее расстояние до 2 + расстояние между вершинами 2 и 4 = 7 + 15 = 22. Поскольку 22<, устанавливаем метку вершины 4 равной 22.
Ещё один сосед вершины 2 — вершина 3. Если идти в неё через 2, то длина такого пути будет = 7 + 10 = 17. Но текущая метка третьей вершины равна 9< 17, поэтому метка не меняется.
Все соседи вершины 2 просмотрены, замораживаем расстояние до неё и помечаем ее как посещенную.
Третий шаг. Повторяем шаг алгоритма, выбрав вершину 3. После ее «обработки» получим такие результаты:
Дальнейшие шаги. Повторяем шаг алгоритма для оставшихся вершин (Это будут по порядку 6, 4 и 5).
Завершение выполнения алгоритма. Алгоритм заканчивает работу, когда вычеркнуты все вершины. Результат его работы виден на последнем рисунке: кратчайший путь от вершины 1 до 2-й составляет 7, до 3-й — 9, до 4-й — 20, до 5-й — 20, до 6-й — 11.
Критерий проверки существования простого цикла в графе G, проходящего через две заданные вершины u и v:
1) после исключения из графа G всех точек сочленения удалить те его компоненты, которые не содержат вершин u и v;
2) в оставшемся подграфе H условие 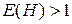 является необходимым и достаточным для существования требуемого простого цикла.
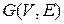(Точками сочленения графа  являются связные, представляющие особо уязвимое звено, так как их утрата приводит к нарушению единства и сплоченности этой организации.
Отметим, что в графе с гамильтоновым циклом нет точек сочленения. )
|
|
|
|
|
|
|
|
|
|
