8.Операции на алгебраических структурах. Группы, подгруппы, нормальные группы, их свойства.

Хорошо известны две операции на множестве Z целых чисел – сложение и умножение. Обобщением понятия операции на произвольном множестве S является отображение , которое называется m-арной операцией на множестве S. При этом постулируется, что образ каждого элемента из  принадлежит множеству S – это так называемое свойство замкнутости операции. Под алгебраической системой или алгебраической структурой понимается некоторое множество S с одной или несколькими операциями на нем.

Среди всевозможных алгебраических систем с одной ассоциативной операцией самыми изученными являются группы. Теория групп – один из старейших разделов абстрактной алгебры, чрезвычайно богатый приложениями.

Группой  называется множество G с бинарной операцией " 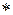", для которой выполнены три следующих условия:

a) операция " 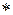" ассоциативна;

b) в G существует единичный элемент (единица) e, такой, что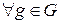

;

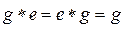c) 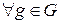существует обратный элемент , такой, что

.

Если к тому же операция " 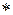" коммутативна, то группа называется абелевой ( коммутативной ). Группа называется конечной или бесконечной в зависимости от числа ее элементов, причем для конечной группы G число ее элементов называется порядком группы и обозначается .

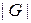Часто  при записи заменяют  или  и называют произведением элементов g и h. Иногда для групповой операции вместо мультипликативной записи используют аддитивную и пишут  вместо , называя этот элемент группы прямой суммой элементов g и h. Аддитивные обозначения обычно резервируют для абелевых групп, используя 0 вместо e, а 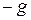 вместо .

Группа, образованная множеством классов вычетов по модулю n, называется группой  классов вычетов по модулю n.

Подмножество H группы G называется подгруппой этой группы, если H само образует группу относительно операции группы G. Подгруппы группы G, отличные от тривиальных групп  и G, называются ее собственными подгруппами. Например, множество всех степеней произвольного элемента h группы G образует подгруппу этой группы. Эта подгруппа порождена элементом h, обозначается 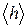 и является, очевидно, циклической. Если 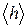– конечная подгруппа, то ее порядок называется порядком элемента h. Он равен наименьшему целому числу k, такому, что k-я степень h равна e.

Обобщением понятия сравнимости по модулю n является

Теорема 1. Если H – подгруппа группы G, то отношение

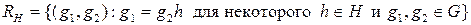
является отношением эквивалентности.

Соответствующие отношению 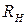 классы эквивалентности называются левыми смежными классами группы G по подгруппе H и обозначаются

.

Аналогично можно определить разбиение группы G на правые смежные классы по подгруппе H

,

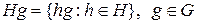которые совпадают с левыми для абелевой группы G.

Если число смежных классов конечно, то оно называется индексом подгруппы H в группе G и обозначается .

Теорема 2. (Теорема Лагранжа). Для подгруппы H конечной группы G

.

Как следствие получаем: порядок подгруппы всегда делит порядок группы. Так как 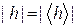, то порядок любого элемента делит порядок группы G.

Подгруппа H группы G называется нормальной в G, если выполнено условие

.

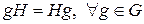Нормальные подгруппы играют особо важную роль в теории групп. Условие 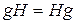 равносильно условию 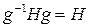. Поэтому говорят, что  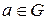сопряжен с  посредством элемента g, если 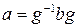. Часто использую степенное обозначение: . Легко проверяются тождества:

.