 |
19. Вершинные и реберные раскраски графа. Хроматический многочлен, хроматическое число и хроматический индекс.
|
|
|
|
19. Вершинные и реберные раскраски графа. Хроматический многочлен, хроматическое число и хроматический индекс.
Пусть n – целое положительное число.
Раскраской гр. G называется раскраска его вершин в n цветов так, чтобы никакая пара смежных вершин не была раскрашена в один цвет.
Граф G называется n-раскрашиваемым, если он имеет вершинную раскраску в n различных цветов. Наименьшее целое k, для которого граф G имеет раскраску своих вершин в k различных цветов, называется хроматическим числом графа G и обозначается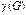 
. Например, легко понять, что граф G является 1-раскрашиваемым тогда и только тогда, когда он не содержит ребер, а 0-раскрашиваемым является только пустой граф.
Для любого положительного целого n число n-раскрасок произвольного графа G совпадает со значением 
хроматического многочлена 
(число способов раскраски графа G в n цветов), который определяется выражением
, где символом 
обозначен остовный подграф графа G с числом ребер S.
для всех положительных целых n, а наименьшее положительное целое m, для которого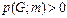 
, равно хроматическому числу 
.
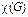Реберная раскраска графа G, при которой никакие ребра одного цвета не должны быть смежными. Наименьшее целое k, для которого граф G имеет реберное раскрашивание в k цветов, называется хроматическим индексом (хроматическим классом, реберно-хроматическим числом) графа G и обозначается 
.
20. Планарность. Формула Эйлера. Теорема Потрягина-Куратовского. Теорема о четырех красках.
Граф G называется планарным (плоским), если его можно изобразить на плоскости так, чтобы все ребра пересекались только в его вершинах. Такое изображение называется плоским топологическим графом. Гранью этого графа называется область плоскости, ограниченная ребрами и не содержащая внутри ни вершин, ни ребер. Множество граней графа G обозначается 
. Для связного плоского топологического графа справедлива формула Эйлера 
.
|
|
|
Справедлива теорема о 4-х краска х: каждый планарный граф G имеет хроматическое число 
.
Теорема Понтрягина – Куратовского гласит, что граф планарен тогда и только тогда, когда он не содержит подграфов K5 или K3, 3
21. Деревья. Матричная теорема о деревьях, подсчет числа остовов.
Граф, не содержащий никаких циклов, называется ациклическим. Его цикломатическое число 
. Ациклический граф также называют лесом, а если к тому же 
, т. е. ациклический граф связный, то он называется деревом. Всякое нетривиальное дерево имеет не менее двух висячих вершин, т. е. вершин степени 1. Порядок дерева T с p вершинами и q ребрами равен p, а из формулы для цикломатического числа следует, что 
.
Остовный подграф графа G, являющийся деревом, называется остовным деревом (остовом, каркасом) графа G.
Если 
– матрица смежности графа G, а диагональная матрица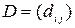 
определена соотношениями: 
и 
при 
, то 
называется матрицей Кирхгофа графа G. В общем случае каждому ребру G сопоставлена проводимость – действительное (комплексное) число. Элемент 
матрицы Кирхгофа 
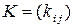равен сумме проводимостей ребер, инцидентных 
, а при элемент 
равен сумме проводимостей ребер, соединяющих вершины и 
. Для матрицы K выполняются соотношения:
, 
.
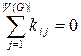Пусть 
получена из матрицы K вычеркиванием строки и столбца, соответствующих вершине r. Тогда имеет место матричная теорема о деревьях
Теорема 1. При произвольной нумерации вершин графа G для матрицы Кирхгофа K справедлива формула
,
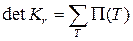где суммирование проводится по всем остовам T графа G, а 
равно произведению проводимостей всех ребер остова T. Для единичных проводимостей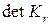 
совпадает с числом остовов графа G.
|
|
|
В частности, из теоремы 1 следует знаменитая теорема Кэли
Теорема 2. Число остовов n-клики равно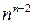 
.
Таким образом, число различных деревьев, построенных на p вершинах, равно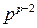 
. Иначе, если каждой вершине дерева произвольно сопоставить некоторое число (метку), то число помеченных деревьев порядка p равно .
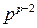Дерево называется " посаженным" (корневым), если одна из его вершин (корень) выделена. Посаженное дерево " растет" из корня, причем остальные вершины могут образовывать поддеревья (внутренние вершины) или не образовывать (висячие вершины или листья). Изображение такого дерева на плоскости называется плоским корневым деревом. Обычно считается, что плоское корневое дерево изображается на плоскости с разрезом, проходящим через корень, а дерево располагается по одну сторону разреза. Два таких дерева называются изоморфными, если одно из них может быть преобразовано в другое непрерывными движениями в полуплоскости.
При описании соотношений между вершинами дерева часто используется терминология, принятая в генеалогических деревьях. Так в дереве или поддереве все вершины являются потомками его корня, и наоборот, корень является предком всех своих потомков. Из теоремы 2 следует, что число корневых помеченных деревьев порядка p равно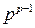 
. Подсчет непомеченных деревьев представляет собой более сложную задачу.
|
|
|
