 |
22.Корневые деревья. Задачи о подсчете корневых деревьев. Высота дерева. Числа Фибоначчи, их свойства.
|
|
|
|
22. Корневые деревья. Задачи о подсчете корневых деревьев. Высота дерева. Числа Фибоначчи, их свойства.
Дерево называется " посаженным" (корневым), если одна из его вершин (корень) выделена. Посаженное дерево " растет" из корня, причем остальные вершины могут образовывать поддеревья (внутренние вершины) или не образовывать (висячие вершины или листья). Изображение такого дерева на плоскости называется плоским корневым деревом. Обычно считается, что плоское корневое дерево изображается на плоскости с разрезом, проходящим через корень, а дерево располагается по одну сторону разреза. Два таких дерева называются изоморфными, если одно из них может быть преобразовано в другое непрерывными движениями в полуплоскости.
С помощью деревьев описываются многие комбинаторные задачи. Знаменитая задача Леонардо Фибоначчи о размножении кроликов может быть перефразирована как задача о росте дерева из корня. Она определяется следующими условиями: каждая новая ветвь первый год только тянется вверх или в сторону, а затем (начиная со второго года) дает по одному боковому побегу; сколько ветвей будет на дереве через 1, 2, 3, … лет?
Несложно заметить, что решения этой задачи находятся с помощью рекуррентного соотношения, определяющего числа Фибоначчи:
 .
.
Из записанного рекуррентного соотношения можно получить производящую функцию, также определяющую числа Фибоначчи
 .
.
В частности, с помощью этой производящей функции находится формула
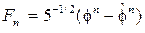 ,
,
где  , а число
, а число 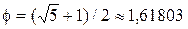 играет важную роль во многих разделах математики. С античных времен в мире искусств оно рассматривалось как эстетически самое благоприятное отношение. Поэтому число f имеет специальное название – отношение золотого сечения.
играет важную роль во многих разделах математики. С античных времен в мире искусств оно рассматривалось как эстетически самое благоприятное отношение. Поэтому число f имеет специальное название – отношение золотого сечения.
|
|
|
Числа Фибоначчи неожиданно появляются, например, при нахождении числа остовов графа G с вершинами 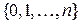 и
и 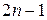 ребрами, задаваемого следующими условиями: ребра G соединяют вершину с номером 0 с каждой из остальных n вершин и k-ю вершину с
ребрами, задаваемого следующими условиями: ребра G соединяют вершину с номером 0 с каждой из остальных n вершин и k-ю вершину с  -й вершиной при
-й вершиной при  . Число остовов графа G совпадает при
. Число остовов графа G совпадает при  с числом Фибоначчи
с числом Фибоначчи  .
.
23. Кубические деревья. Числа Каталана, их свойства.
Корневое дерево называется кубическим, если каждая его вершина, кроме корня и листьев, имеет степень три. Для подсчета числа таких деревьев рассмотрим следующую комбинаторную задачу, связанную с именем бельгийского математика Каталана. При помощи n умножений вычисляется произведение переменных  . Найти число способов
. Найти число способов  расстановки скобок в произведении
расстановки скобок в произведении  так, чтобы порядок умножений был полностью определен.
так, чтобы порядок умножений был полностью определен.
В качестве примера приведем одну расстановку скобок в произведении  :
: 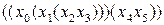 . Эту расстановку скобок можно закодировать двоичным кодом 11010100100, присваивая при чтении произведения слева направо символ " 1" каждой встречаемой левой скобке, символ " 0" каждой встречаемой переменной и опуская все правые скобки.
. Эту расстановку скобок можно закодировать двоичным кодом 11010100100, присваивая при чтении произведения слева направо символ " 1" каждой встречаемой левой скобке, символ " 0" каждой встречаемой переменной и опуская все правые скобки.
Приведенная расстановка скобок отвечает кубическому графу рисунка 1,

на котором висячие вершины, соответствующие перемножаемым переменным, помечены меткой " 0", а внутренние вершины, соответствующие левым скобкам, помечены меткой " 1". Польский математик Лукасевич предложил следующее правило для вычисления двоичного кода такого плоского корневого кубического дерева: дерево проходится по часовой стрелке, начиная от корня; если при прохождении вершина встречается в первый раз, то записывается ее метка: " 0" или " 1"; если – во второй, то ничего не записывается. Например, дереву, изображенному на рисунке 1 соответствует двоичный код 11010100100.
Таким образом, установлена биекция между множеством способов расстановки скобок в произведении переменных  и множеством плоских корневых кубических деревьев с
и множеством плоских корневых кубических деревьев с  -й висячей вершиной, причем последнему выполняемому знаку умножения, стоящему между
-й висячей вершиной, причем последнему выполняемому знаку умножения, стоящему между 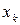 и
и  , отвечает
, отвечает 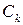 способов расстановки скобок в
способов расстановки скобок в  и
и 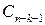 способов – в
способов – в  .
.
|
|
|
Поэтому искомое число способов  расстановки скобок в произведении
расстановки скобок в произведении  равно числу плоских корневых кубических деревьев и удовлетворяет рекуррентному соотношению
равно числу плоских корневых кубических деревьев и удовлетворяет рекуррентному соотношению
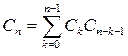 ,
,
представляющему собой свертку последовательности 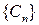 .
.
С помощью полученной формулы находится производящая функция
 ,
,
позволяющая выразить числа Каталана  через биномиальные коэффициенты
через биномиальные коэффициенты
 .
.
Будем изображать два ребра, инцидентных всем вершинам степени 3, плоских корневых кубических деревьев, " растущими" вверх или налево, или направо. Биекция между таким множеством деревьев с n листьями и множеством плоских деревьев с n ребрами и висячим корнем устанавливается по правилу Бернхарта: все ребра кубического дерева, " растущие" направо, стягиваются в точку. Например, кубическому дереву рисунка 1 отвечает дерево рисунка 2
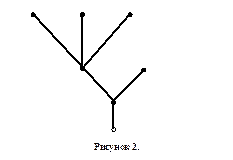
Двоичный код такого дерева находится по следующему правилу: дерево проходится против часовой стрелки, начиная от корня; если ребро проходится первый раз, то записывается " 0", если второй – " 1"; в записанном кодовом слове символ " 1", стоящий на последнем месте, отбрасывается и полученный код заменяется на сопряженный (двоичное слово записывается справа налево).
Например, для рисунка 2 после его прохождения против часовой стрелки получим двоичный код: 001001010111. После отбрасывания последней единицы и замены слова на сопряженное находим код 11010100100, совпадающий с кодом кубического дерева, изображенного на рисунке 1.
Таким образом, число плоских деревьев с n ребрами и висячим корнем также определяется значением  .
.
Числа Каталана также появляются в задаче Эйлера триангуляции выпуклого многоугольника: требуется подсчитать число способов его разделения на треугольники с помощью непересекающихся диагоналей.
Во многих играх, программировании, теории кодирования и т. п. используются бинарные деревья. Такое дерево T либо пусто, либо состоит из корня и двух бинарных поддеревьев: левого –  и правого –
и правого –  . Каждая вершина бинарного дерева может иметь 0, 1, 2 поддерева, и существует различие между левым и правым поддеревьями.
. Каждая вершина бинарного дерева может иметь 0, 1, 2 поддерева, и существует различие между левым и правым поддеревьями.
|
|
|
В прикладных задачах, описываемых с помощью деревьев, часто требуется найти оптимальный, в некотором смысле, путь от корня к листьям.
|
|
|


