 |
Специфику адсорбции составляет внутри-дифузионный процесс.
|
|
|
|
Специфику адсорбции составляет внутри-дифузионный процесс.
1. 3. 1. Внутри-диффузионная кинетика адсорбции
Экспериментальное изучение кинетики адсорбции обладает внешней простотой. Известны две схемы выполнения этого исследования. Они иллюстрированы рис 1. 9. Согласно первой из них (рис. 1. 9 а) гранулу «чистого» адсорбента помещают в трубочку-«перекладину» Н-образного прибора. В «стоячках» прибора двигаются потоки газа. Левый, например, поток – это смесь газа-носителя и газа-метки, диффузию которого изучают. Правый поток – чистый газ-носитель. Метка диффундирует через гранулу и ее концентрацию измеряют на входе в левый «стоячек» (С0) и на выходе из правого (С1). Скорость миграции метки (Р) описывают первым законом Фика:
Р = - DS (dС/dl), или (1. 6)
Р = De S (dХ/dl), (1. 6а)
где D - коэффициент диффузии, выраженный в концентрационных единицах подвижной фазы, De - эффективный коэффициент диффузии, выраженный в концентрационных единицах неподвижной фазы, S – площадь гранулы, нормальная к направлению диффузии, l – координата по длине гранулы. Предполагается, что значения С и Х равновесны. Заменяя производные конечными разностями, например, dС/dl = (С0 – С1)/L, где L – длина гранулы, вычисляют D и De. Соотношение между ними, очевидно, такое: De = D/(dХ/dС), или для линейной изотермы:
De = D/Г (1. 7),
где Г – коэффициент Генри. Размерность коэффициентов диффузии – м2/с.
Недостаток схемы, приведенной на рис. 1а, заключается в том, что в опытах, выполненных по этой схеме, в сущности, измеряется коэффициент проницаемости сквозных транспортных пор в грануле. Тупиковые поры, в том числе микропоры, в которых происходит адсорбция, этой методикой не учитывается.
|
|
|
Можно поступить по-другому: прикрепить, например, к коромыслу весов гранулу и поместить ее в поток несорбирующегося газа, содержащего адсорбтив в концентрации Со (см. рис. 1. 9б) Начнется процесс адсорбции – весы будут фиксировать постепенное увеличение веса гранулы. Оно будет продолжаться до тех пор, пока величина адсорбции не достигнет значения, равновесного концентрации адсорбтива в потоке. Обозначим текущую величину адсорбции через Х, равновесную - через Хо. Тогда отношение γ = Х/Хо есть степень отработки емкости сорбента, а ее зависимость от времени [γ = γ (t), где t - время], называемая кинетической кривой, - кинетическая характеристика процесса.
Математический аппарат для обработки кинетической кривой и вычисления ее параметра – коэффициента диффузии заимствован из теории теплопроводности. Процесс диффузии в однородное сферическое зерно адсорбента, подобный процессу нагрева (охлаждения) однородной сферической гранулы, при тех начальных условиях, которые были названы в тексте, записывается дифференциальным уравнением, которое носит название второго закона Фика:
∂ С/∂ t = D[∂ 2C/∂ r2 + (2/r)(∂ C/∂ r)] (1. 8. ) 
В этом уравнении: С – концентрация адсорбата в газовой фазе гранулы адсорбента, r – текущий радиус гранулы. Решение (1. 8. ) при линейной изотерме адсорбции дает следующее интегральное выражение:
γ = Х/Хо = 1 – (6/π 2) Σ (exp( – n2Fo)/n2 ), (1. 9. )
где n = 1, 2, 3, … - ряд целых натуральных чисел, Fo - критерий Фурье: Fo = π 2De. t/R2, R, - радиус гранулы. Имеются изящные приемы вычисления De из уравнения (1. 9) по известным парным значениям γ и t, т. е. из кинетических кривых. Для гранул иных форм, чем сферическая, получены аналогичные соотношения.
|
|
|
Определенные в ходе опытов значения D и De не вполне корректны. Они получены в предположении, что изотермы адсорбции линейны. Между тем, они, как правило, выпуклы. Адсорбция всегда идет с выделением тепла. Расчет же коэффициентов осуществляется в предположении, что процесс адсорбции изотермичен. Но самое главное - это непригодность экспериментально измеренных коэффициентов для прямого прогнозирования переноса в других системах и условиях, чем те, которые были использованы в опытах. Чтобы такое прогнозирование оказалось возможным, необходимы модели структуры адсорбентов и модели переноса вещества в них. Рассмотрим этот вопрос более подробно.
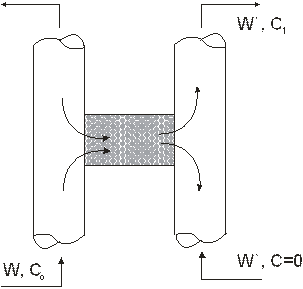
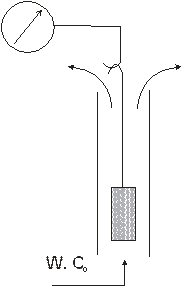
Рис. 1. 9. Две установки для экспериментального изучения кинетики адсорбции
Промышленный адсорбент содержит поры разного размера. В простейшем случае в рассмотрение следует включить адсорбирующие (микро-) и транспортные поры. Можно принять, что перенос вещества в микропорах характеризуется размером зоны микропористости (для цеолита – радиусом кристаллита), равным r, и эффективным коэффициентом диффузии в микропористости (первичной пористости) - De1 Перенос в транспортных порах (во вторичной пористости) характеризуется радиусом гранулы R и коэффициентом диффузии D2.
Будем считать, что перенос в первичной пористости - простое явление и не носит составного характера. В этом случае De1 – единственная диффузионная характеристика этого вида переноса. Для транспортных пор известны, по меньшей мере, две составляющие: перенос по поверхности этих пор и перенос в их объеме. Это параллельные виды переноса и суммарный коэффициент диффузии записывается следующим образом:
D2 = Dv + Г. Des, (1. 10)
Dv – коэффициент диффузии в объеме вторичных пор, Des – эффективный коэффициент диффузии по поверхности вторичных пор. Перенос в объеме вторичных пор, видимо, происходит по механизму нормальной диффузии, коэффициенты (Dн) которой широко представлены в литературе. В значения коэффициентов надо внести поправку на порозность гранулы (ε ) и извилистость каналов. Доказывается, что
Dv=(ε /K2)Dн (1. 11)
Перенос в транспортных порах и в микропорах - последовательные виды переноса и они должны суммироваться через сложение сопротивлений. Строгое определение диффузионного сопротивления отсутствует, но, по здравому смыслу, оно должно быть пропорционально времени пребывания молекул в рассматриваемой среде: t1 – в адсорбирующих порах и t2 – в транспортных порах Для адсорбирующей пористости время пребывания (t1) пропорционально r2/ De1, а для транспортной t2 ~ R2/ D2. Сложение времен дает оценку общего времени пребывания в двух видах пористости (Т):
|
|
|
Т = t2 + t2 ~ R2/ D + r2 /De1. Г (1. 12).
Будем рассматривать общее время пребывания в качестве меры диффузионного сопротивления гранул. Иногда величину, обратно пропорциональную общему времени пребывания, называют кинетическим коэффициентом: КК = 1/Т. Его записывают в форме неразложимого комплекса КК = (D/R2). Обратим внимание, что уравнение (1. 12) и кинетический коэффициент не содержат некоторого «общего» коэффициента диффузии и принципиально не могут его содержать. Это связано с тем, что у исследователя отсутствуют данные об эффективном (кажущемся) размере гранулы с разными видами пористости, в которых протекают последовательные переносы вещества.
1. 3. 2. Внешне-диффузионная кинетика адсорбции
Подвод вещества из ядра потока к поверхности адсорбента описывают теми же соотношениями, какими описывают любой процесс массообмена на границе «поток-стенка». Уравнения кинетики в некотором огрублении имеют вид:
(dX/dt) = β *ex f (C – Cх*) = β ex(C –Cх*) (1. 13. )
В этих уравнениях: X - величина адсорбции, г/м3 ; t - время, с; C и Cх* - текущая концентрации адсорбата в потоке и концентрация, равновесная величине адсорбции на поверхности раздела фаз, г/м3; f- внешняя удельная поверхность гранул, м2/м3; β *ex - коэффициент внешней массоотдачи, отнесенный к единице поверхности раздела фаз, м/с; β ex - коэффициент внешней массоотдачи, отнесенный к единице объема слоя, 1/с.
Для вычисления коэффициентов внешней массоотдачи используют критериальные уравнения вида:
|
|
|
Nue = A ReemScn, (1. 14. )
где Ree - модифицированный критерий Рейнольдса, вычисленный по эквивалентному диаметру прохода; Sc - критерий Шмидта и Nue– модифицированное число Нуссельдта, вычисленное по эквивалентному диаметру прохода, A, m, n – коэффициенты критериального уравнения, значения которых определяются гидродинамическим режимом в зернистом слое. Граничным значениям гидродинамических режимов в зернистом слое соответствуют следующие значения критерия Рейнольдса: ламинарный режим Ree < 2, переходной режим 2 < Ree < 30 и турбулентный режим, который реализуется при значениях критерия Рейнольдса более высоких, чем 30.
Информация, относящаяся к уравнениям (1. 13. ) и (1. 14. ), широко представлена в литературе по химической инженерии.
1. 3. 3. Смешанно-диффузионная кинетика адсорбции
Уравнение кинетики смешанно-диффузионного процесса часто записывают так:
(dX/dt) = β o(C – C*), (1. 15)
где β о – общий коэффициент массопередачи, С* - концентрация адсорбата в потоке, равновесная средней концентрации его в адсорбенте. Смысл прочих параметров уравнения (1. 15. ) и их размерности см. в уравнении (1. 13. ).
Считают, что общий коэффициент массопередачи есть величина, обратная общему сопротивлению в системе, которое складывается из сопротивления внешней массоотдачи и сопротивления внутренней массоотдачи. Для адсорбции правило аддитивности сопротивлений не доказано, но на практике оно часто используется. Иногда в число сопротивлений включают сопротивление, эквивалентное продольным квазидиффузионным эффектам. Так называют факторы, понижающие эффективность массообмена из-за неидеальной структуры потока в зернистом слое адсорбента. Запишем уравнение аддитивности сопротивлений:
(1/β о) = (1/β ех) + (1/β in) + (1/β d), (1. 16. )
где β in – кажущийся коэффициент внутренней массоотдачи, β d - коэффициент массоотдачи, эквивалентный продольно-диффузионным эффектам. Размерности всех коэффициентов уравнения (1. 16. ) – 1/с.
Очень часто адсорбционный процесс длится долго. Доказывается, что при больших временах (Fo = 1 и более), когда всеми слагаемыми уравнения (1. 9), кроме первого, можно пренебречь, общее время пребывания адсорбата в грануле и коэффициент внутренней массоотдачи связаны примерным соотношением, которое носит название уравнения Глюкауфа. В нашей записи, ориентированной на использование уравнения (1. 12. ), оно имеет вид:
β in = 15 /Т = 15(D/R2) (1. 17. ).
Это соотношение позволяет оценить второе слагаемое уравнения (1. 16).
|
|
|
При «ленгмюровской» изотерме адсорбции, как показали Тодес и Биксон, для сопротивления, обусловленного продольно диффузионными эффектами, справедливо следующее уравнение:
(1/β d) = D*/W2, (1. 18. )
где W – скорость потока, D*- коэффициент продольной диффузии, вычисляемый по справочным данным и значениям критериев Рейнольдса и Шмидта (см. в примере Р. 4).
Приведенный выше материал позволяет рассчитать параметры, характеризующие кинетику адсорбции. Но качество этого расчета трудно признать удовлетворительным. Кинетика адсорбции – слабо разработанная область теории адсорбции. Поэтому расчетные значения коэффициентов диффузии, массоотдачи и массопередачи в ней часто рассматривают в качестве оценочных параметров и, если необходимо, уточняют их в специальных технологических экспериментах.
|
|
|


