Расчеты к подразделу 1.4.5.

    Р. 14. Рассчитать минимальный расход греющего газа (воздуха) для десорбции воды из цеолита. Адсорбент стабилен при температурах до 650 °С. Прочие условия таковы: h = 1, 3 кДж/м³. К, Н = 5, 04. 10² кДж/м³. К, Х*_n =1, 3. 10² кг/м³, ∆ H = 4200 кДж/кг, W = 0, 2 м/с.

Из-за высокой стабильности цеолитов температуру газа, вводимого на регенерацию, определяют по термостабильности материалов и элементов конструкции. Обычно она не превышает 300-350 °С. Примем, что температура газа равна 320 °С. Тогда ∆ Т = 320 – 20 = 300 К. Для определения скорости движения фронта подставим параметры в уравнение (1. 32):

 

U_td = Wh/[H +h + (∆ H. X*_n/∆ T)] = 0, 2. 1, 3/[5, 04. 10² + 1, 3 + (4200. 1, 3. 10²/300)] =

 

= 1, 1.. 10^-4м/с.

 

Определим также минимальное количество газа, которое следует подать при регенерации:

 

ПВ_td= W/U_td = 0, 2/1, 1. 10^-4  = 1, 8. 10³ м³ /м³.

 

Эта цифра в четыре с половиной раза превышает расход газа на нагрев слоя, не содержащего адсорбат.

 

    Р. 15. (Самостоятельная работа) Аналогичные расчеты выполнить для силикагеля, предел термостабильности которого составляет 250 С. Теплоту десорбции воды из силикагеля принять равной 2800 кДж/кг. Сравнить скорости движения фронтов десорбции и минимальные удельные расходы газа на регенерацию силикагеля и цеолита.

 

1. 4. 6. Динамика адсорбции смесей

 

    Если коэффициенты распределения компонентов смеси, вычисленные по изотермам индивидуальной адсорбции, различаются на порядок и больше, то вместо динамики адсорбции смеси рассматривают динамику индивидуальной адсорбции целевого компонента. Ошибка, связанная с пренебрежением адсорбцией других компонентов не превышает 10%, что допустимо в технических расчетах. Если компоненты смеси имеют близкие значения коэффициентов распределения (коэффициент разделения близок к единице), то введение поправок на множественность адсорбатов становится необходимым.

    Равновесная адсорбция компонентов смеси. Приводим без обоснования упрощенную схему расчета совместной адсорбции нескольких веществ для случая, когда индивидуальная равновесная адсорбция каждого из них описывается выпуклой изотермой адсорбции. Основным уравнением в этой схеме является уравнение Люиса, которое ниже записано для адсорбции бинарной смеси:

 

(Х₁₂ /Х⁰₁) + (Х₂₁ /Х⁰₂ ) = 1,                               (1. 34)

 

где Х₁₂ – величина адсорбции первого компонента смеси при содержании его в объемной фазе С₁ в присутствии второго компонента, Х₂₁ – величина адсорбции второго компонента смеси при содержании его в объемной фазе С₂ в присутствии первого компонента, Х⁰₁ – величина индивидуальной адсорбции первого компонента при содержании его в объемной фазе С = С₁ + С₂, Х⁰₂ – величина индивидуальной адсорбции второго компонента при содержании его в объемной фазе С = С₁ + С₂. В уравнении (1. 34) величины индивидуальной адсорбции предполагаются известными; они определяются из изотерм индивидуальной адсорбции, а определению подлежат величины адсорбции компонентов смеси. (При расчете адсорбции смесей концентрации и емкости выражают не в весовых, а в мольных единицах).

    Уравнение (1. 33) решают совместно с выражением для коэффициента разделения (Кр):

 

Кр = (Х₁₂/С₁)(С₂/Х₂₁)                          (1. 35)

        

Коэффициент разделения слабо зависит от состава, давления и температуры и предполагается известной величиной. Его находят либо из экспериментальных данных, либо вычисляют по эмпирическому уравнению:

lgKp = -0, 23 + 4, 76(1 – φ ), где φ – отношение коэффициента аффинности в уравнении ТОЗМ хуже сорбирующегося вещества к коэффициенту аффинности вещества, адсорбирующегося лучше.

    Для смесей, число компонентов (N) в которых более двух, в уравнение Льюиса включают дополнительные слагаемые, а коэффициенты разделения определяют для всех возможных пар присутствующих компонентов.

    Если изотермы индивидуальной адсорбции компонентов смеси описываются уравнениями Генри, то адсорбцию каждого из них считают независимой от адсорбции других присутствующих веществ. Это разумное допущение, так как в области Генри степень заполненности адсорбционного пространства невелика (≈ 1% и менее) и адсорбирующиеся вещества не вытесняют друг друга.

Динамика адсорбции. При линейных изотермах сорбции, в соответствии с приведенным выше допущением, компоненты смеси сорбируются независимо и фронт каждого из них передвигается по слою со своей характерной скоростью, определяемой уравнением (1. 21). Расчет ведут по скорости движения целевого компонента, присутствие которого в очищенном газе не допускается.

    Для выпуклых изотерм адсорбции модели и решения представлены только для изотермической динамики адсорбции. Математическая модель по форме не отличается от модели (М3), но, конечно, намного сложнее, так как для каждого компонента смеси должны быть записаны все уравнения модели. Отмечается, что прямой расчет невозможен и вычисления проводят путем последовательных приближений.

 Феноменологию процесса, следуя Дубинину и Явичу, принято рассматривать в квазистационарном приближении. На рис. 1. 24 приведены кривые распределения концентраций адсорбатов в потоке для двухкомпонентной смеси. На этом рисунке сплошная линия отвечает распределению концентраций лучше сорбирующегося компонента, а пунктирная – компонента, сорбирующегося хуже. Отметим, что фронт хуже сорбирующегося компонента всегда опережает фронт компонента, который адсорбируется лучше. В зоне ОА слой равновесно насыщен обоими компонентами при концентрациях в потоке С₀₁  и С₀₂, отвечающих их

 

 

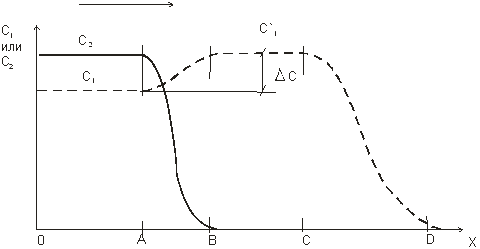
    Рис. 1. 24. Кривые распределения концентраций в объемной фазе адсорбента для адсорбции бинарной смеси.

 

содержанию в газе, поступающему на очистку. В зоне АВ происходит падение концентрации компонента 2 из-за его адсорбции. В этой же зоне концентрация хуже сорбирующегося компонента 1 возрастает до значения С’₀₁ > C₀₁. Рост концентрации связан с вытеснением компонента 1 компонентом 2 в зоне АВ. Зона ВС насыщена первым компонентом, а его адсорбция происходит в зоне СД.

 

 

 

    Рис. 1. 25. Кривые распределения концентраций в фазе адсорбента при адсорбции бинарной смеси компонентов.

 

    На рис. 1. 25 изображены кривые распределения концентраций в фазе адсорбента. Из сопоставления рис. 1. 24 и рис. 1. 25 видно, что адсорбция первого, хуже сорбирующегося компонента, определяется его свойствами, вытекающими из индивидуальной изотермы адсорбции этого вещества. Единственное, хотя и очень существенное отличие от индивидуальной адсорбции, состоит в том, что эти свойства соответствуют не концентрации С₀₁, в которой этот компонент присутствует в потоке, а концентрации С’₀₁, превышающей исходную на величину ∆ С = С’₀₁ – С₀₁ из-за вытеснения первого компонента вторым в зоне 0А. Адсорбция второго компонента определяется свойствами, которые определяются совместной адсорбцией второго и первого компонентов.          

Обычно концентрация вещества в объемной фазе значительно меньше величины адсорбции. Поэтому для квазистационарного перемещения фронтов можно записать:

           U₁= WC’₀₁/X’₁(C’₀₁ )                           (1. 36)

 

            U₂ = WC₂ /X₂₁                                                   (1. 37)             

 

В этих уравнениях U₁ и U₂ – скорости движения первого и второго фронтов адсорбции.

    Скорость движения фронта вытеснения первого компонента из зоны сорбции второго, очевидно, равна скорости движения фронта сорбции второго компонента. Поэтому можно записать:

 

U₂ = WС ₂/Х₂₁ = W(С’₁ – С₀₁ )/(Х′ ₀₁ (С’₀₁ ) – Х₁₂)                (1. 38)

 

Совместное решение уравнения (1. 38) и уравнения изотермы индивидуальной адсорбции первого компонента позволяет определить концентрацию этого компонента в объемной фазе и равновесную ей величину его адсорбции. После этого находятся скорость движения фронта первого компонента.

    Предельная возможность слоя определяется тем, какой из компонентов смеси является целевым. Если это первый компонент смеси, то ее вычисляют из уравнений (1. 23) и (1. 36). Если второй – из уравнений (1. 23) и (1. 37).

 

⇐ Предыдущая567891011121314Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: