 |
Расчеты к подразделу 1.4.4
|
|
|
|
Р. 11. Продолжим задачу об осушке метана при 6 МПа цеолитом NaA и определим режим переноса фронтов и разогрев в ходе адсорбции. Исходные данные, необходимые для решения задачи таковы: Со = 3, 3. 10-2 кг/м3, Х*о = 1, 3. 102 кг/м3, Н = 504 кДж/(м3. К), h = 120 кДж/(м3. К), W = 0, 2 м/с, ∆ Н = 4200 кДж/кг (теплота адсорбции воды на цеолите).
1. Определим скорость движения тепловой волны:
Ut = Wh/(H + h) = 0, 2. 120/(504 + 120) = 3, 8. 10-2 м/с.
2. Определим скорость движения концентрационного фронта:
Uc = WCo/(X*o + Co) = 0, 2. 3, 3. 10-2 /(1, 3. 102 + 3, 3. 10-2) = 5, 1. 10-5 м/с.
3. Скорость движения тепловой волны примерно в тысячу раз больше скорости движения концентрационного фронта – в слое реализуется режим одиночной тепловой волны.
3. Разогрев равен:
∆ T = ∆ H. X*o/(H + h + h(X*o +Co)/Co)=
=4200. 1, 3. 102 /(504 +120 + 120(1, 3. 102 +3, 3. 10-2) /3, 3. 10-2) = 1, 2 K.
Адсорбция воды из потока метана при 6 МПа протекает в изотермических условиях.
Р. 12. Метан осушается цеолитом при атмосферном давлении. Теплоемкость метана в этих условиях равна: h = 2, 0 кДж/м3К; прочие параметры процесса см. в Р. 11. Определить режим движения волн и разогрев.
1. Скорость движения тепловой волны:
Ut= 0, 2. 2, 0/(504 + 2) = 8. 10-4 м/с
2. Скорость движения концентрационной волны не изменилась: Uс = 5. 10-5 м/с
3. Так как скорость движения тепловой волны превышает скорость движения волны концентрационной, реализуется режим одиночной тепловой волны.
4. Разогрев в слое:
∆ T = 4200. 1, 3. 102/(504 +2 +2(1, 3. 102 + 3, 3. 10-2 )/3, 3. 10-2) = 65 К.
Процесс неизотермический и, если начальная температура слоя составляет 20 С. то из слоя будет выходить поток с Тmax = 20 + 65 = 85 С.
Р. 13. Поток водорода очищают от азота в слое цеолита. Определить режим, если давление составляет 1 МПа, содержание азота равно 10 %, а емкость адсорбента по азоту равна 4, 5 нм3/м3, а теплота адсорбции азота составляет 750 кДж/м3
|
|
|
1. Теплоемкость газа при 1 МПа примерно равна 13 кДж/м3 К, теплоемкость адсорбента – 504 кДж/м3 К. При скорости потока 0, 1 м/с скорость движения тепловой волны составит:
Ut = 0, 1. 13/(504 +13) = 2, 5. 10-3 м/с
2. Содержание азота 10 % при давлении 1 МПа соответствует его концентрации в газе 1 нм/м3. Отсюда скорость движения концентрационной волны:
Uс = 0, 1. 1/(4, 5 + 1) = 2. 10-2 м/с.
3. Скорость движения концентрационной волны выше, чем собственная скорость волны температурной – в слое произошло образование режима комбинированных волн. Разогрев газа и адсорбента теплом сорбции составляет:
∆ Т = ∆ Н. Х*/(Н + h) = 750. 4, 5/(504 + 13) = 6, 5 К
1. 4. 5. Динамика адиабатической десорбции
Рассмотрим слой, равновесно насыщенный адсорбатом при Т = Тn. Пусть в некоторый момент времени (t = 0) в слой начинает поступать поток, температура которого То > Tn. Начнется десорбция адсорбата и вынос его из слоя. Эти процессы отвечают восстановлению поглотительных свойств адсорбента, утраченных им в ходе прямого процесса очистки потока. Несмотря на первостепенную важность процессов восстановления и теоретически, и экспериментально они изучены крайне слабо.
В адиабатическом приближении модель динамики десорбции подобна модели динамики адсорбции (М5). Формально изменились лишь условия однозначности. Их следует записать так:
Начальные условия: t = 0, 0 ≤ x ≤ L, C = Cn, X = X*n, Tg = Ta = Tn,
Граничные условия: t > 0, x = 0, C = Co < Cn, Tg= Tgo> Tn.
Они констатируют, что в слой поступает поток, концентрация примеси в котором ниже, чем в объемной фазе слоя, а температура выше, чем температура адсорбента и объемной фазы. В таких условиях, естественно, идет процесс десорбции.
Качественные особенности протекания тепло- и массообменных процессов в слое представлены на рис1. 22 и рис. 1. 23.
|
|
|
Как видно на рис. 1. 22, из слоя в течение некоторого промежутка времени (0А) выходит поток, концентрация примеси в котором и температура отвечают начальным условиям. Затем следует небольшой подъем температуры (участок АВ) при практически неизменной
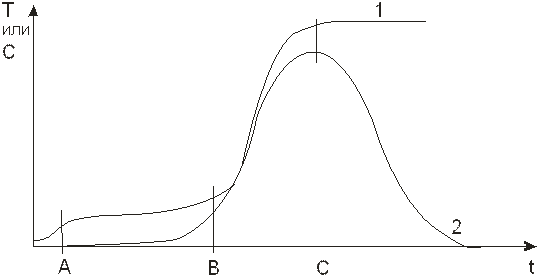
Рис. 1. 22. Выходные кривые при адиабатической десорбции: 1 –температурная кривая, 2 – концентрационная кривая.

Рис. 1. 23. Кривые распределения температур и концентраций для адиабатической десорбции (обозначения см. на рис. 1. 22).
концентрации примеси в выходящем потоке. В точке В температура и концентрация примеси в выходящем потоке начинают резко возрастать. Рост прекращается в точке С, после которой концентрация примеси начинает понижаться, а температура остается на постоянном уровне. Аналогичные участки присутствуют на кривых распределения, показанных на рис. 1. 23.
Начальный скачок температуры в точке А обусловлен тем, что адсорбат, десорбированный в головных зонах слоя, частично повторно адсорбируется в зонах замыкающих. Так как процесс адсорбции сопровождается выделением тепла, температура слоя и потока на выходе из адсорбера несколько повышаются. Основная десорбция происходит в зоне нагрева участка слоя. Десорбированное вещество выделяется в объемную фазу. Распределение его по слою имеет характер пика, площадь которого возрастает по мере увеличения количества десорбата.
Важной особенностью процесса является квазистационарный режим перемещения температурной кривой. В этом отношении температурная кривая в процессе с десорбцией существенно отличается от температурных кривых простого процесса нагрева (без десорбции). Пример этих кривых был приведен на рис 1. 11. Они имели тенденцию к неограниченному «размазыванию» по слою. Причина различий состоит в том, расход тепла на десорбцию задерживает перемещение головных участков температурных кривых. В результате температурная кривая сжимается и перемещается по слою почти как «обрывный» фронт. Запишем тепловой баланс для элемента слоя длиною ∆ l, на который сместился тепловой фронт за время ∆ t:
∆ H (X*n ∆ l) + (H +h)∆ l ∆ T = W∆ t h ∆ T
Первое слагаемое этого уравнения отвечает расходу тепла на десорбцию примеси. Второе – нагреву элемента слоя и находящейся в нем объемной фазы. Выражение в правой части отражает подвод тепла потоком.
|
|
|
Выполним подстановки и преобразования, подобные тем, которые были использованы при выводе уравнения (1. 30), и в результате получим уравнение для скорости движения температурного фронта при десорбции:
Utd = Wh/[H + h + ∆ HX*n/∆ T)] (1. 33)
В этих уравнениях: ∆ Т – разность между температурой потока, вводимого в слой, и начальной температурой слоя. Из (1. 32) определяется предельная возможность при адиабатической десорбции: ПВtd= W/Utd:
ПВtd = [(H + h)/h] + [∆ H. X*n /(h. ∆ T)], (1. 32*)
Или, что то же самое, минимальный расход потока на нагрев и десорбцию. Он, как видно из уравнения (1. 32), уменьшается при увеличении температуры греющего поток, т. е. зависит не только от свойств, но и от условий осуществления процесса.
|
|
|


