 |
Расчеты к разделу 1.3.
|
|
|
|
Р. 4.. Определить общий коэффициент массопередачи при адсорбции воды гранулированным цеолитом NaA из потока метана. Адсорбция происходит при 25 С и давлении 6 МПа, скорость потока в слое цеолита составляет 0, 2 м/с. Гранулы адсорбента имеют шарообразную форму; их диаметр составляет 3 мм. Содержание воды в метане 3, 3. 10-2 кг/м3 .
1. В справочниках приведены значения физических свойств метана при 25 °С и 6 МПа:
- плотность ρ = 43, 4 кг/м3 ;
- вязкость μ = 1, 3. 10-5 кг/(с. м);
- коэффициент нормальной диффузии Dn= 4, 9. 10-7 м2/с.
2. По уравнению ТОЗМ, приведенному в разделе 1. 2., рассчитаем величину адсорбции воды при 25 С и С = 3, 3. 10-2 кг/м3. Ради экономии, расчет не приводится. Результат его таков: Хо = 1, 3. 102 кг/м3
3. Определим эквивалентный диаметр сферических гранул цеолита: de = (2ε d)/[3(1 –ε )] = (2. 0, 4. 3)/[3(1-0, 4)] = 0, 67 мм.
4. Критерий Рейнольдса и гидродинамический режим в зернистом слое адсорбента. Критерий Рейнольдса равен:
Ree = (Wdeρ )/μ = 0, 2. 0, 67. 10-3. 43, 4/1, 3. 10-5 = 470.
Согласно данным монографии М. Э. Аэрова и О. М. Тодеса (Гидравлические и тепловые основы работы аппаратов со стационарным м кипящим зернистым слоем, Л., «Химия». 1968), граничное значеиие критерия Рейнольдса для турбулентной области в зернистом слое равно 30. Процесс протекает в турбулентном режиме, для которого коэффициенты уравнения (1. 14) таковы: A = 0, 395, m = 0, 64, n =0, 333.
5. Критерии Шмидта и Нуссельдта.
Sc = μ /(ρ Dn) = 1, 3. 10-5/(43, 4. 4, 9. 10-7 = 0, 64.
Nu = ARemScn = 0, 395. 8700, 640, 640, 33 =37, 4.
6. Определим коэффициент внешней массоотдачи:
β *ex = Nu. Dn/de = 37, 4. 4, 9. 10-7/1, 3. 10-3 = 1, 41. 10-2 м/с.
Удельная внешняя поверхность гранул составляет: f=6/d =6/3. 10-3 = 2. 103 м2/м3. Отсюда коэффициент внешней массоотдачи, отнесенный к единице объема слоя, равен:
|
|
|
β ех = β *ехf = 1, 41. 10-2. 2. 103 = 28, 2 1/с.
7. Определим по уравнению (1. 12) коэффициент диффузии в объеме транспортных пор гранулы адсорбента:
Dv2 = (ε /Ki2)Dn = (0, 5/1, 52)4, 9. 10-7 = 1, 1. 10-7 м2/с.
8. Информация о диффузии по поверхности транспортных пор отсутствует. Можно считать, что приведенное выше значение есть минимальная оценка коэффициента диффузии в транспортных порах: D2 > Dv2. . Отсюда время пребывания молекул воды в транспортной пористости не превышает t2 = R2 /D2 = ((1, 5. 10-3)2/(1, 1. 10-7) =20 с.
9. В монографии Д. П. Тимофеева Кинетика адсорбции М., 1962 приведено значение эффективного коэффициента диффузии воды в кристаллах цеолита NaA: De1 = 0, 6. 10-10 м2/с. Отсюда время пребывания в адсорбирующих порах (в первичной пористости) равно:
t1 = r2/De1Г =(1, 5. 10-6)2 / ((0, 6. 10-10). 3, 9. 103) = 1. 10 –5 с.
Здесь: 1, 5. 10-6 м – радиус частиц кристаллита. Считают, что в случае нелинейных изотерм адсорбции, к которым относится изотерма адсорбции воды на цеолите, возможна приближенная замена Г на К = Х/С0 = 3, 9. 103.
10. Общее время пребывания молекул адсорбата в грануле цеолита:
Т = t1 + t2 = 1. 10-5 + 20 = 20 с.
Лимитирующим сопротивлением в рассмотренном примере является сопротивление транспортных пор.
11. Найдем β in по уравнению (1. 17. ):
β in = 15/Т= 15/20 = 0, 75 1/с.
12. Найдем диффузионный критерий Пекле (Ре). Для его определения используем диаграмму, приведенную на стр. 229 монографии М. Э. Аэрова и О. М. Тодеса. Согласно этой диаграмме, при Re = 470 и Sc = 0, 64 критерий Ре = 2.
13. Определим коэффициент продольной диффузии:
D*= Wde/Pe = 0, 2. 1, 3. 10-3/2 = 1, 3. 10-4 м2/с.
14. Определим коэффициент массоотдачи, отвечающий продольной диффузии:
β d = W2/D* = 0, 22/(1, 3. 10-4) = 308 1/с.
15. Рассчитаем сумму диффузионных сопротивлений и найдем коэффициент массопередачи:
(1/β о) = (1/β ex) + (1/β in) + (1/β d) = (1/28, 2) + (1/0, 75) +1/308) = 1, 3 с,
|
|
|
β о = 0, 75 с-1
Процесс адсорбции в рассмотренном нами случае лимитируется внутренней диффузией, которая в свою очередь определяется диффузией в транспортных порах цеолита.
1. 4. Конвективный тепло-массообмен в неподвижном зернистом слое
1. 4. 1. Объекты рассмотрения
Как правило, адсорбционные процессы проводят, пропуская поток через слой неподвижного зернистого адсорбента. При контактировании потока с зернами происходит адсорбция примесей и очистка потока. Это конвективный массообмен в неподвижном зернистом слое. Адсорбция сопровождается выделением тепла. Иногда оно невелико и можно считать, что массообмен протекает в изотермических условиях. В большинстве случаев выделение тепла значительно и адсорбцию следует рассматривать как совмещенный тепло-массообмен в зернистом слое.
В ходе адсорбции происходит насыщение адсорбента примесями и он постепенно утрачивает свою очистительную способность. Ее восстанавливают, пропуская через слой поток нагретого газа. Это тоже процесс конвективного тепло-массообмена: нагрева адсорбента и десорбции примеси. И наконец, нагретый адсорбент перед повторным использованием охлаждают потоком холодного чистого газа. Это процесс теплообмена. Таким образом, тепло- и массообмен в неподвижном зернистом слое – суть многих технологических адсорбционных процессов.
Конвективный тепло- массообмен в зернистом слое часто называют динамикой (динамикой адсорбции, динамикой нагрева, охлаждения и т. п. ). Это самый распространенный вариант осуществления адсорбционных процессов. Мы увидим, что содержание тепло-массообмена в зернистом слое составляют перемещения температурных и концентрационных фронтов (волн). Поэтому динамику процессов переноса в зернистом слое часто называют фронтальной динамикой.
Объектом рассмотрения будет являться цилиндрический аппарат (адсорбер), в котором находятся гранулы адсорбента. Начало координат х = 0 поместим в плоскости ввода потока. Начальным условиям будет отвечать адсорбент, равномерно насыщенный адсорбатам. (Частным случаем равномерной насыщенности является слой, не содержащий адсорбат). В тепловых задачах начальному условию обычно отвечает слой с постоянной температурой.
|
|
|
В некоторый момент времени t = 0 в слой с расходом W начинает поступать поток, который содержит адсорбат в иной концентрации, чем слой, или имеет температуру, отличающуюся от температуры слоя. Начинаются процессы тепло-массообмена. Будем считать, что концентрация адсорбата в поступающем потоке и его температура не изменяются в течение всего периода пропускания. Концентрация и (или) температура в слое и на выходе из него изменяются из-за протекания массообменных и(или) теплообменных процессов. Определение закономерностей их протекания и составляет основную задачу динамики адсорбции.
Методом решения задач динамики тепло-массообмена является математическое моделирование. Структура моделей и вид уравнений баланса обосновываются в курсах математической физики. Уравнения равновесия и кинетики задает технолог. Решения моделей редко имеют аналитическую форму. Обычно результаты получают в численном виде. Они могут использоваться непосредственно или в виде «сверток» в некоторые приближенные соотношения.

Рис. 1. 10. Зернистый слой – объект рассмотрения.
Такая процедура решения задач по тепло-массообмену в зернистом слое связана с большими затратами времени и труда. Поэтому, наряду с нею, существуют некоторые приближенные приемы. Они вытекают из математических моделей, хотя и являются их сильным упрощением. Эти приближенные приемы полезны, когда решается принципиальный вопрос: возможен или нет некоторый процесс очистки или разделения? Он позволяет затем, по мере получения положительных предварительных оценок, переходят к решениям повышенного уровня сложности.
1. 4. 2. Нагрев (охлаждение) зернистого слоя и динамика изотермической адсорбции при линейной изотерме адсорбции
Эти две задачи можно рассматривать одновременно, так как в математическом отношении они очень схожи.
Математическая модель конвективного нагрева (охлаждения) зернистого слоя имеет вид:
Wh(∂ Tg/∂ x) + H(∂ Ta/∂ t) + h(∂ Tg/∂ t) = 0
|
|
|
∂ Ta/∂ t = α (Tg – Tg*) (M. 1)
T*g = Ta
Начальные условия:
t = 0, 0 < x < L; Tg =Ta = Tn
Граничные условия:
t > 0, x = 0; нагрев Tg > Tn = To; охлаждение Tg < Tn = To.
В этих уравнениях: W – скорость потока, h – теплоемкость потока, H – теплоемкость гранул твердого тела (адсорбента), α – коэффициент температуропроводности, L – длина слоя, Tg – текущая температура потока, Ta – текущая температура твердого тела, Tg* - температура потока, равновесная текущей температуре твердого тела, Tn – начальная температура в слое, To – температура потока, поступающего в слой, x – координата длины слоя, t – время.
Первое уравнение системы (М. 1) – уравнение скоростей изменения теплосодержания (тепловой баланс) в фазах системы. Оно записано с некоторыми упрощениями, основные из которых – это пренебрежение продольной теплопроводностью в слое и потерями тепла в окружающую среду. Второе уравнение – уравнение переноса температуры. Установлено, что процессы переноса тепла (температуры) в зернистом слое, как правило, лимитируются внешней теплоотдачей. Последнее уравнение представляет собой условную запись теплового «равновесия» в системе. Очевидно, что при теплообмене «равновесие» между фазами тождественно равенству их температур. Соотношения однозначности формализуют то качественное описание, которое было приведено в подразделе 1. 4. 1.
Запишем также уравнения математической модели динамики изотермической адсорбции при линейной изотерме адсорбции. Будем предполагать, что адсорбируется только один компонент потока, концентрация которого так мала, что переход вещества из потока в адсорбент не сопровождается тепловыми эффектами и не приводит к изменению скорости потока. В этом случае:
W(∂ C/∂ x) + ∂ X/∂ t + ∂ C/∂ t = 0
∂ X/∂ t = β 0(C – C*) (M/2)
X = Γ C*
Начальные условия:
t = 0, 0 < x < L; C = Cn (0), X = Xn (0). (Значения в скобках – часто встречающийся случай с так называемыми нулевыми начальными условиями).
Граничные условия:
t > 0, x = 0; C = Co.
В этих уравнениях: Г – коэффициент Генри, β о- общий коэффициент массопередачи, С – текущая концентрация адсорбата в потоке, Х – текущая концентрация адсорбата в адсорбенте, C* - концентрация адсорбата в потоке, равновесная его концентрации в адсорбенте, Cn - концентрация адсорбата в объемной фазе к моменту начала процесса, Co - концентрация адсорбата в потоке, входящем в слой, X n - концентрация адсорбата в адсорбенте к началу процесса. Смысл уравнений системы (М. 2) подобен смыслу уравнений, входящих в систему (М. 1).
|
|
|
Системы (М. 1) и (М. 2) имеют аналитическое решение. Оно сложно по структуре и его не часто используют в технологических расчетах. Это решение, однако, удобно для изучения особенностей протекания процессов. Их иллюстрируют рис. 1. 11. а и 1. 11. б. В момент времени, отличный от нулевого в слой начинает поступать поток. Направление движения потока обозначено на рис. 1. 11 стрелкою. Так как температура (или концентрация адсорбата) в потоке выше, чем температура (или начальная концентрация) в слое, в нем начинают протекать процессы тепло- или массообмена. Из-за конечной скорости переноса тепла (массы) процессы не мгновенны и в слое образуются некоторые кривые распределения температур (концентраций). На рис. 1. 11а они приведены для возрастающих моментов времени. Как видно из рисунка, кривые распределения (синонимы: фронты, волны) перемещаются


Рис. 1. 11. Нагрев зернистого слоя или адсорбция при линейной изотерме адсорбции: а – распределения температур или концентраций в моменты времени t1 < t2 < t3; б – выходная кривая для слоя длиною L.

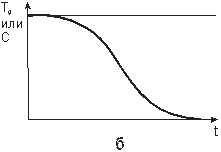
Рис. 1. 12. Охлаждение зернистого слоя или десорбция при линейной изотерме адсорбции: а – кривые распределения, б – выходная кривая.
по слою в направлении, совпадающем с направлением движения потока. При этом их протяженность непрерывно изменяется; она возрастает прямо пропорционально t1/2
В некоторый момент времени (его называют моментом проскока, временем защитного действия) повышенная температура (концентрация) появляются на выходе из слоя и анализатор, установленный в его выходном сечении, начнет фиксировать непрерывное изменение потенциала. Зависимость изменений температуры (концентрации) от времени приведена на рис 1. 11. б. Она носит название выходной кривой.
На рис. 1. 12. аналогичные данные приведены для процессов охлаждения слоя (десорбции адсорбата).
С точки зрения технолога, основной интерес представляют выходные кривые, так как именно они говорят о том, как скоро слой будет нагрет (охлажден) или насыщен адсорбатом (освобожден от него). На основании тех точных решений, которые были упомянуты выше, для модели (М2) были получены приближенные соотношения. Ниже представлено одно из приближенных соотношений - уравнение Жуховицкого, Забежинского, Тихонова для изотермической адсорбции вещества при линейной изотерме адсорбции:
t0, 5 = (LΓ /W)0, 5 – Ф(y). (Г/β o)0, 5 (1. 19. )
В этом уравнении: Ф(у) – вероятностная функция относительной концентрации адсорбата в потоке (у), которая носит название обратной функции Крампа, у = (С - Сn)/(Сo - Сn). Эта функция табулирована и ее значения приведены в математических справочниках и некоторых пособиях по адсорбции. Отметим, что при у = 0, 5 имеем Ф(у) = 0; При у < 0, 5 Ф(у) положительна, а при у > 0, 5 она отрицательна.
Функциональное содержание формулы (1. 19. ) заключается в определении времени (t) появления за слоем длиною (L) некоторой относительной проскоковой концентрации адсорбата (у). Эта концентрация рассматривается в качестве предельно допустимого остаточного содержания примеси в потоке. Возможна и обратная постановка задачи: определение длины слоя, который обеспечивает некоторое предельное содержание примеси в потоке в течение заданного времени.
Уравнение (1. 19. ) получено для прямой задачи массообмена – для адсорбции. Но подобие процессов адсорбции и десорбции при линейной изотерме адсорбции позволяют распространить его на обратную задачу, т. е. на десорбцию. В этом случае между слагаемыми уравнения будет стоять знак «+». Его можно применять также для решения задач, связанных с конвективным нагревом или охлаждением слоя. В этих задачах параметр Г уравнения заменяется отношением теплоемкостей [(H + h)/h)], а общий коэффициент массопередачи будет заменен общим коэффициентом температуропроводности (α ).
На рис. 1. 13 в координатах «у-х» повторно изображена одна из кривых распределения концентраций (а) и выходная кривая (б). Нанесем на кривую распределения точку уц (Сц) и проведем через нее вертикальную линию. Площади, образованные кривой распределения и линиями построения, обозначим F1, F2, F3. Пусть относительная концентрация уц в данный момент времени t находится на расстоянии L от места ввода потока в слой. Очевидно, что количество адсорбата, накопленного в слое длиною L, пропорционально площади F3. Площадь F2 пропорциональна количеству адсорбата, которое не уловлено в слое рассматриваемой длины и ушло за его пределы, а площадь F1 – количеству адсорбата, которое в этом слое не поглотилось к моменту времени t, но поглотится, если время будет более значительным. Аналогичные построения можно выполнить для выходной кривой, и соответствующие площади на ней означены через F*.

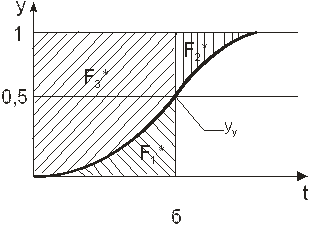
Рис. 1. 13. К определению скорости движения центра тяжести: а – кривая распределения концентраций, б – выходная кривая.
Сумма F3 + F 2 пропорциональна количеству вещества, введенному в слой адсорбента. Сумма F 3 + F 1 – количеству адсорбата, которое может быть поглощено в слое рассматриваемой длины. Таким образом:
F3 + F2 ~ WSC0t,
F3 + F1 ~ (LSX*0 +LSC0),
|
|
|


