 |
где S – площадь поперечного сечения слоя, X*0 – величина адсорбции, равновесная концентрации адсорбата в поступающем потоке.
|
|
|
|
где S – площадь поперечного сечения слоя, X*0 – величина адсорбции, равновесная концентрации адсорбата в поступающем потоке.
Выберем такое положение точки уц (Сц), для которого F1 = F2 . Ее можно назвать центром тяжести кривой распределения (выходной кривой). Для нее из приведенных выше соотношений имеем:
WC0t = L(X*0 + C0) (1. 20)
Отношение L/t = Uс следует рассматривать как скорость движения центра тяжести кривой распределения по слою:
Uс = WC0/(X*0+ C0) (1. 21)
Так как все величины, входящие в правую часть уравнения (1. 21) – постоянные, то скорость движения этой и только этой точки постоянна. Для других концентрационных точек она будет меняться со временем, что приводит, как было показано на рис. 1. 11., к постепенному увеличению протяженности кривой распределения.
Вернемся к уравнению (1. 19. ). Условие постоянства отношения L/t (скорости движения) для него выполняется, если Ф(у = 0, 5) = 0. Значит, координата центра тяжести в рассматриваемых случаях есть у = 0, 5. Относительные концентрации, не равные 0, 5, передвигаются по слою быстрее (у < 0, 5) или медленнее (y > 0, 5), чем центр тяжести, что и приводит к постепенному увеличению протяженности кривой распределения.
Вывод о постоянстве скорости движения центров тяжести кривых распределения справедлив для фронтов разных форм и разной природы. Он соблюдается при теплообмене и массообмене, для процессов прямых и обратных, для линейной и любых других изотерм адсорбции. Это универсальное свойство движущихся волн. Его использование облегчает грубый расчет (оценку) конвективных процессов в зернистом слое.
Преобразуем уравнение (1. 21) в следующую форму:
|
|
|
Uс /W = C0/(X*0+ C0) (1. 22. )
Умножив числитель и знаменатель левой части уравнения на S – площадь сечения слоя и t - время, мы получаем отношение объема слоя (V = LS) к количеству газа (Q = WSt), которое через слой следует пропустить, чтобы на выходе из него появился центр тяжести кривой распределения. Обратную величину этого отношения можно назвать предельной возможностью слоя при массообмене. Обозначим ее как ПВс:
ПВс = W/Uс = (X*0 + C0)/C0 = К (1. 23. )
Она, как видно из уравнения (1. 23), равна коэффициенту распределения.
Аналогичным образом могут быть получены выражения для скорости движения центра тяжести тепловой волны и предельной возможности слоя при теплообмене (ПВt):
Ut =Wh/(H + h) (1. 24. )
ПВ t= W/Ut = (H + h)/h, (1. 25. )
Ut – скорость движения центра тяжести тепловой волны.
Адсорбция – процесс очистки и технолога, как правило, интересуют возможности слоя, отвечающие концентрациям более низким, чем концентрация в центре тяжести волны. По отношению к ним предельная возможность, даваемая уравнением (1. 23. ), является максимальной возможностью. Она говорит о том, какое максимальное количество потока можно очистить единицей объема адсорбента. Практическая возможность, конечно, будет ниже ее.
При нагреве или охлаждении слоя точка глубокого нагрева (охлаждения) всего слоя лежит ближе к входному сечению слоя, чем центр тяжести, и предельная возможность в задачах теплообмена является минимальной возможностью. Она говорит о том, какое минимальное количество потока надо ввести в единицу объема слоя, чтобы его нагреть или охладить. Практическое количество потока будет превышать минимальное.
Таким образом, предельные возможности – это приближенные оценки технологических характеристик, или оценки по порядку величин. Их ценность состоит в очень простом определении даже в крайне непростых для точного расчета случаях.
|
|
|
Расчеты к подразделу 1. 4. 2
Р. 5. Теплоемкость двухатомных газов при атмосферном давлении составляет h = 1, 25 кДж/м3. К; теплоемкость адсорбента равна H = 0, 96 кДж/кг. К. Определить минимальное количество воздуха с температурой 20 °С, которое необходимо пропустить через слой объемом 15 м3, имеющим начальную температуру 200 °С, чтобы охладить слой, и самую высокую температуру слоя после такого охлаждения.
1. Изменим размерность H:
Н = 0, 96. ρ а = 0, 96. 600 = 580 кДж/м3. К, где ρ а = 600 кг/м3 – насыпная плотность адсорбента.
2. Определим предельную возможность, которая является минимальной; она равна:
ПВt = (Н + h)/h = (580 +1, 25)/1, 25 = 460 м3/м3
3. Для охлаждения 15 м3 слоя потребуется воздуха не менее 15. 460 = 6900 м3 .
4. Самая высокая температура слоя будет находиться в сечении, противоположном сечению ввода охлаждающего воздуха. При пропускании того количества, которое было определено выше, в этом сечении будет находиться центр тяжести тепловой волны, для которого у = 0, 5. По определению имеем:
у = (Т – Т0)/(Тn – Т0 ) = 0, 5
0, 5 = (Т – 20)/(200 – 20);
Т = 110 °С.
Р. 6. В слой некоторого сорбента, объем которого составляет 15 м3, ввели поток. В нем находится нежелательный компонент, адсорбция которого на данном адсорбенте характеризуется коэффициентом Генри Г = (Х*о + С0)/С0 = 1000 м3/м3 . Определить предельную возможность слоя в удалении нежелательной примеси и максимальное количество очищенного потока.
1. Для 1 м3 имеем: ПВс = Г = 1000 м3/м3 .
2. Для 15 м3 имеем: 15. 1000 = 15000 м3 – таково максимально возможное количество очищенного потока.
Р. 7. В условиях примера Р. 6 определить практическое количество очищенного потока, если остаточное содержание нежелательного компонента в очищенном потоке не должно превышать 0, 05 С0. Коэффициент массопередачи принять равным β 0 = 1, 09 1/с, скорость потока 0, 2 м/с, сечение 4 м2. Начальным содержанием адсорбата в адсорбенте пренебречь.
Подстановкой в правую и левую части уравнения (1. 19) произведения (SW)1/2 придадим ему следующую форму:
Q1/2 = (VΓ )1/2 – Ф(y). (WSГ/β )1/2
1. По условию задачи у = 0, 05. Найдем Ф(у) по таблице, приведенной в пособии Е. Н. Серпионова. Промышленная адсорбция газов и паров. М., «Высшая школа», 1969, стр. 87. При указанном значении у имеем: Ф(у) = 1, 19.
|
|
|
2. Подставим условия задачи в модифицированное уравнение:
Q1/2 = (15. 1000)1/2 – 1, 19. (0, 2. 4. 1000/1. 09)1/2 = 95, 38 м3/2, или Q = 9100 м3. Практическое количество очищенного потока примерно на 40 % ниже максимально возможного, определенного в предыдущем расчете.
Обратим внимание на то, что расчет практического количества очищенного потока потребовал задания ряда конструктивных параметров, тогда как расчет максимального базировался только на свойствах системы. Таким образом, эти два расчета относятся к разным этапам проектирования: расчет максимального к более раннему этапу, а расчет практического к более позднему.
Р. 8. Слой нагретого адсорбента охлаждают потоком, скорость которого составляет 0, 2 м/с. Поток содержит нежелательную примесь, которая не адсорбируется нагретым адсорбентом, но поглощается в слое после охлаждения. Теплоемкости потока и адсорбента приведены в примере Р. 5. Будет ли одновременно с охлаждением идти процесс адсорбции, если Г = 1000? Если Г= 100?
1. Найдем скорость движения концентрационного фронта при Г =1000.
Uс = W/Г =0, 2/1000 = 0, 0002 м/с
2. Найдем скорость движения теплового фронта:
Uе = Wh/(Н + h) = 0, 2. 1, 25/(580 + 1, 25) = 0, 00043 м/с.
Скорость движения теплового фронта примерно в два раза больше, чем концентрационного. Поэтому в слое образуется некоторая зона, в которой адсорбент уже охлажден, но еще не насыщен примесью. Охлаждение будет сопровождаться очисткой, хотя, возможно, и неэффективной.
3. При Г = 100 скорость движения концентрационного фронта составит: Uс = 0, 002 м/с. Скорость движения теплового фронта приведена в п. 2. Она примерно в 5 раз выше скорости движения концентрационного фронта. В слое отсутствуют условия для образования холодной зоны ненасыщенного адсорбента. В этих условиях охлаждение не сопровождается очисткой.
1. 4. 3. Динамика изотермической адсорбции при произвольной изотерме адсорбции
Общий подход. Динамика изотермической адсорбции при произвольной изотерме адсорбции рассматривается при тех же допущениях, что и динамика при линейной изотерме. Запись математической модели (система уравнений (М3)) во всех отношениях, кроме уравнения равновесия, приведенного в третьей строчке системы, подобна записи системы (М2). Уравнение равновесия в систему (М3) включено в общем виде.
|
|
|
W(∂ C/∂ x) + ∂ X/∂ t + ∂ C/∂ t = 0
∂ X/∂ t = β 0(C – C*) (М3)
X = X(C*)
Будем считать, что начальные и граничные условия в системах (М2) и (М3) одинаковы.
Система (М3) аналитического решения не имеет. Ее решают численными методами. Систему уравнений (М3) приводят к разностной форме. Для этого слой длиною L разбивают на m-интервалов, ожидаемую общую продолжительность адсорбции t - на n-интервалов. Для i-го интервала по длине и j-го по времени при использовании простейшей разностной схемы уравнения системы (М3) будут записываться так:
W(Cij – Ci-1-1,, j )/hi + (Xij – Xi, j-1)/hj + (Cij – Ci, j-1 )/hj = 0
(Хij - Х i – 1, j)/hi = β 0(Cij – C*ij)
Xij = X(Cij)
В этих уравнениях hi, hj - шаги по времени и длине.
Система в конечных разностях состоит из трех уравнений и содержит три подлежащие определению переменные: Сij, С*ij и Хij, Она, следовательно, решается. После определения значений переменных в точке ij проводится переиндексация. Индексы i и j присваивают следующей точке, отстоящей на один шаг дальше по координатам t или L, а прежняя точка, ранее имевшая индексы іј получает индексы i-1, j, если сдвиг производится по координате t, или i, j-1, если сдвиг произведен по координате L. В новой точке рассчитываются новые значения переменных. Далее делается следующая переиндексация, еще одна и т. п. до тех пор, пока значения переменных ни будут рассчитаны во всем поле значений L – t.
В качественном отношении решения модели (М3) хорошо согласуются с экспериментальными данными. Количественное соответствие улучшают путем подгонки значений параметра β 0. Причина, из-за которой именно этот параметр принимают в качестве подгоночного, указана в разделе 1. 3.
В левой части рис. 1. 14 приведены кривые распределения концентраций по слою адсорбента для так называемых выпуклых изотерм адсорбции. К этому типу относятся, в частности, изотермы, описываемые уравнениями Ленгмюра и ТОЗМ. Для них характерен более быстрый рост величин адсорбции в области малых давлений, чем в области больших. Пример выпуклой изотермы приведен в правой части рисунка.
|
|
|

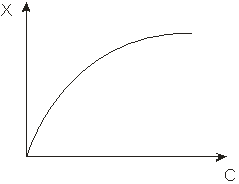
Рис. 1. 14. Кривые распределения (t 1 < t 2 < t3 ) и выпуклая изотерма адсорбции.
На рис. 1. 15. приведены аналогичные кривые для изотерм вогнутых. Для них, как видно из правого рисунка, характерен сравнительно медленный рост величин адсорбции в области малых концентраций и быстрый – в области больших. Сопоставление кривых распределения на рис. 1. 14 и рис. 1. 15 говорит о том, что общие закономерности протекания


Рис. 1. 15. Кривые распределения (t1 < t2 < t3) и вогнутая изотерма адсорбции.
адсорбционного процесса для этих изотерм различны. При выпуклой изотерме кривые распределений с течением преобразуются в некоторое компактное распределение. При вогнутой наблюдается тенденция к неограниченному росту протяженности распределения.
Выкладками, подобными тем, которые были выше приведены для линейной изотермы, можно показать, что скорости движения концентрационных точек, отвечающих центрам тяжести, в случае и выпуклых, и вогнутых изотерм описываются уравнением:
Uc = WC0 /(X*0 + C0) = W/K, (1. 21)
где К – коэффициент распределения. Аналогичным образом предельные (максимальные) возможности равны: ПВс = К. Хотя для выпуклой и вогнутой изотерм скорости движения центра тяжести и максимальные возможности в принципе могут быть одинаковы, практические возможности, относящиеся к головным участкам кривых распределения, для выпуклых изотерм, как правило, выше, чем для вогнутых. Иными словами, при прочих равных условиях выпуклая изотерма обеспечивает сравнительно более высокий съем очищенного потока и по этой причине является предпочтительной.
Путем «свертки» очень большого объема расчетной информации Жуховицкий, Забежинский и Тихонов получили следующие интерполяционные уравнения для выпуклых изотерм при нулевых начальных условиях (t = 0, 0 ≤ x ≤ L, C = X = 0):
Ленгмюровская изотерма:
t = (X*0/WC0){L – (W/β 0) [ln((C0/C) – 1)/p + ln(C0/C) –1]}, (1. 26)
где р = С0/Сˆ, Сˆ – концентрация адсорбата в потоке, равновесная величине Х = 0, 5 Хm;
Прямоугольная изотерма (так называют идеализированную изотерму адсорбции, для которой можно записать: С > 0, Х = Хm =const):
t = (X*0/WC0)[L – (W/β 0)(ln(C0/C – 1)] (1. 27).
Равновесное приближение. Общий подход не содержит явных указаний на причины, в силу которых в системах с разными типами изотерм адсорбции кривые распределения ведут себя по-разному. Ответ на этот вопрос представляет познавательный интерес, полезен в расчетах и часто необходим в выборе адсорбентов. Он решается в рамках равновесного приближения. Исключим из системы (М3) уравнение кинетики, предположив, что β 0 → ∞. В этом случае С – С* → 0 и С ≈ С*. При таких допущениях модель приобретает вид:
W(∂ C/∂ x) + ∂ X/∂ t + ∂ C/∂ t) = 0
X =Х (C) (M. 4).
Решения системы (М4) при тех же условиях однозначности, которые были записаны выше, получены Викке в форме уравнений для скоростей движения фронтов. Они таковы:
- для С = const, Uf = WC0/(X*0 + C0) (1. 28)
- для C ≠ const, Uc = W/(1 + Х′ (C)) (1. 29)
Уравнение (1. 28) по другим, но схожим поводам, неоднократно представлялось выше. Оно носит название уравнения Вильсона и описывает движение «обрывного» (С = const) концентрационного фронта. Он движется по слою с постоянной скоростью Uf . «Обрывный» фронт и его перемещения показаны на рис. 1. 16.
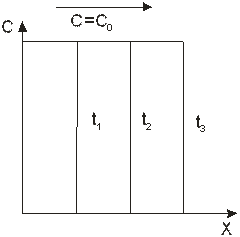
Рис. 1. 16. Движение по слою «обрывного» концентрационного фронта.
Уравнение (1. 29) носит название уравнения Викке. Оно говорит о том, что при отсутствии «обрывного» фронта каждая концентрационная точка кривой распределения концентраций передвигается по слою со своей характерной скоростью Uс, значение которой зависит от производной изотермы адсорбции (Х′ (С)) в этой концентрационной точке.
При нелинейной изотерме адсорбции значения производной непостоянны: они уменьшаются с ростом концентрации, если изотерма выпуклая, и возрастают в случае изотермы вогнутой. Соответственно в «необрывном» фронте и выпуклой изотерме концентрационная точка, отвечающая высокой концентрации, будет двигаться быстрее, чем точка низкой концентрации. При вогнутой изотерме и прочих одинаковых условиях по слою быстрее передвигается слою точка, отвечающая низкой концентрации. Кривые, приведенные на рис. 1. 17, отражают эти особенности процесса для выпуклой (а) и вогнутой (б) изотерм.
Итак, при вогнутой изотерме адсорбции и том направлении движения потока, которое обозначено на рис. 1. 17 стрелкой, первоначальное размытое распределение концентраций в слое становится еще более размытым: в ходе движения фронта градиент концентраций уменьшается. В тех же условиях при выпуклой изотерме концентрационные точки, отвечающие высоким концентрациям, постепенно догоняют точки низких концентраций. Градиент концентраций возрастает до тех пор, пока в слое ни образуется «обрывный» фронт. С момента его образования все концентрационные точки, т. е. фронт в целом, передвигаются по слою с одной и той же скоростью, значение которой дается уравнением Вильсона. Для вогнутой изотермы, таким образом, наблюдается полное качественное соответствие между предсказаниями моделей (М3) и (М4). Для выпуклой изотермы полное соответствие отсутствует: из модели (М3) следует, что в своем предельном состоянии фронт компактен, но размыт, из (М4), что он предельно компактен – «обрывный».
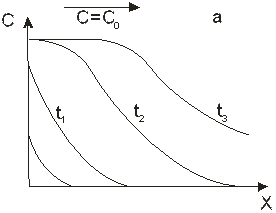
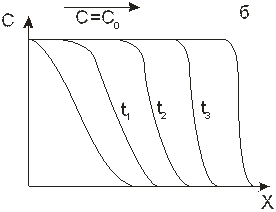
Рис. 1. 17. Кривые распределения концентраций в равновесной динамике адсорбции при вогнутой (а) и выпуклой (б) изотермах.
Отметим, что при изменении направления движения потока на противоположное направление фронт сжимается при вогнутой изотерме адсорбции и расширяется при выпуклой. Эти ситуации отвечают обратному процессу – десорбции.
Квазистационарное приближение. Неполное соответствие кривых распределения, полученных из моделей (М3) и (М4), при выпуклых изотермах адсорбции было объяснено Зельдовичем. Суть объяснения сводится к следующему. Из-за конечной скорости массообменных процессов размывание кривых распределения идет всегда. При вогнутой изотерме оно усугубляется размывающим эффектом, который обусловлен видом изотермы адсорбции. При выпуклой изотерме размывающий эффект конечной скорости массообмена, наоборот, компенсируется сжимающим эффектом, обусловленным видом изотермы. В слое достаточно большой протяженности и выпуклой изотерме эффекты размывания и сжатия компенсируют друг друга и по слою, начиная с некоторого момента времени, с постоянной скоростью передвигается фронт постоянной протяженности и постоянного профиля. Скорость его движения описывается уравнением Вильсона, что естественно, так как в состав этого фронта входит центр тяжести. Такой режим переноса фронта носит название квазистаионарного.
Существование квазистационарного режима переноса фронта сорбции было зафиксировано уже в ранних работах (Шилов с сотр. ) по динамике адсорбции. Причины и условия его возникновения были непонятны, но сам факт его реализации позволил разработать сравнительно простые приемы расчета процесса. К числу их относятся уравнение Шилова, концепция зоны массопередачи (высоты работающего слоя) и некоторые другие подходы. Некоторые из них обсуждаются в общеинженерных курсах.
|
|
|


