Расчеты к подразделу 1.4.3

    Р. 9. Рассчитать продолжительность осушки метана цеолитом NаА, длина слоя которого составляет L = 3 м. Остаточную концентрацию воды в газе принять равной С = 10 мг/м³. Прочие условия процесса осушки приведены в примере Р. 4: начальная концентрация воды в метане С₀ =3, 3. 10^-2 кг/м³; равновесная величина адсорбции Х*₀= 1, 3. 10²кг/м³; скорость потока W = 0, 2 м/с; общий коэффициент массопередачи β ₀ =1, 09 1/с.

Изотерма адсорбция воды на цеолитах имеет почти прямоугольную конфигурацию. Поэтому продолжительность процесса может быть рассчитана по уравнению (1. 26):

 

 

t = (X*₀/WC₀) [L – (W/β ₀) (ln(C₀/C) –1)] =

 

(1, 3. 10²/0, 2. 3, 3. 10^-2) [ 3 – (0, 2/1, 09)(ln(3, 3. 10^-2/10^-6) – 1)] = 3. 10⁴ c ≈ 8 ч.

 

 

    Р. 10. На приведенном ниже рисунке, который повторяет рис. 1. 6, приведены изотермы адсорбции воды на среднепористом (1) и микропористом (2) силикагелях. Руководствуясь данными этого рисунка определить, какой из этих силикагелей следует выбрать для организации адсорбционного процесса осушки газа. Принять, что относительная влажность φ =100 % соответствует концентрации воды в газе, поступающем на осушку, равной 20 г/м³

1. Если ориентироваться на максимальную возможность адсорбентов:

 

ПВ_c= K = (X*₀ + C₀)/C₀ ,

 

то предпочтение будто бы должно быть отдано среднепористому силикагелю. Действительно, при φ = 100 % (С₀ =20 г/м³) его равновесная активность более чем в 1, 5 раза превышает равновесную активность мелкопористого силикагеля, Соответственно, возможность этого адсорбента, рассчитанная по концентрации воды в газе, поступающем на осушку, будет больше в сравнении с силикагелем мелкопористым. Увы, этот вывод неверен.

 

 

       Изотермы адсорбции воды средне- (1) и микропористым (2) силикагелями

 

2. Изотермы адсорбции воды на силикагелях имеют сложную конфигурацию: начальный участок изотерм выпуклый, средний вогнутый, а замыкающий снова выпуклый. В соответствии с концепциями, изложенными в подразделе «Равновесное приближение», кривые распределения адсорбата по слою также будут иметь сложную конфигурацию. В головной части распределения будет расположен почти обрывный участок, отвечающий первому выпуклому участку изотермы адсорбции. За ним будет следовать размытый участок кривой распределения (средний интервал концентраций) и снова – почти обрывный участок. Гипотетическое распределение концентраций для выпукло-вогнутой-выпуклой изотермы адсорбции, которая характерна для системы вода-силикагель, изображено на рисунке.

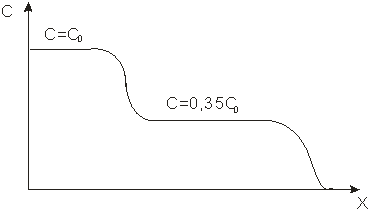
Гипотетическое распределение концентраций воды в слое силикагеля

 

3. В соответствии с п 2, расчет максимальных возможностей должен выполняться по точке перегиба на изотерме адсорбции, разделяющей первый выпуклый и вогнутый участки.

    Эта точка лежит при φ =35 % для обоих силикагелей (С =7 г/м³). При этой концентрации величина адсорбции воды на мелкопористом силикагеле в 2 раза превышает величину адсорбции на силикагеле среднепористом. Предельные возможности силикагелей, рассчитанные по концентрации и величине сорбции в точке перегиба, будут различаться в такое же количество раз. Для адсорбции воды следует выбрать мелкопористый силикагель.

 

1. 4. 4. Динамика адиабатической адсорбции

Общий подход. Если концентрация примеси в потоке значительна, то ее адсорбция сопровождается выделением тепла, что приводит к увеличению температуры потока и адсорбента. Адсорбция приобретает характер неизотермического процесса. В пренебрежении потерями тепла в окружающую среду и теплообменом со стенкою адсорбера можно говорить о адиабатическом процессе, или динамике адиабатической адсорбции. Очевидно, что изотермический процесс – это предельный случай процесса адиабатического, при котором тепловыделения в слое пренебрежимо малы. Поэтому все допущения модели изотермической, кроме особенностей тепловыделения и теплообмена, распространяются на модель адиабатической сорбции. Общая запись ее такова:

 

W(∂ C/∂ x) + ∂ X/∂ t + ∂ C/∂ t = 0

 

Wh(∂ T_g/∂ x) + H(∂ T_a/∂ t) + h(∂ T_g/∂ t) + ∆ H(∂ X/∂ t) = 0

 

X = X(C*, T_a)                                                    (М. 5)

 

∂ X/∂ t = β ₀(C –C*)

 

                          ∂ T_a/∂ t=α ₀(T_g-T*_g)                                      

 

Первое уравнение этой модели – уравнение материального баланса адсорбата. По записи оно не отличается от аналогичных уравнений предшествующих моделей. Второе уравнение – тепловой баланс; в отличие от аналогичного уравнения модели (М1), оно содержит слагаемое, которое отвечает приходу тепла в результате адсорбции. Характеристикой этого источника является теплота адсорбции - ∆ Н (кДж/г). Третье уравнение – политерма равновесной адсорбции. Она представляет собой семейство изотерм адсорбции, отвечающих разным температурам. Вид изотерм в этой задаче обычно не рассматривается. Но скрыто предполагается, что все они являются выпуклыми. Четвертое и пятое уравнения – это соответственно уравнения кинетики сорбции и теплообмена. Все параметры и переменные, которые входят в систему (М5), кроме ∆ Н, были определены в ранее рассмотренных моделях.

    Начальные условия: t = 0, 0 ≤ x ≤ L, C = X =0, T_g= T_a = T_n.

       Граничные условия: t > 0, x = 0, C = C₀, X = X(C₀, t), T_g = T_g0, T_a = T_a(t).

    Многие параметры, входящие в систему (М5), зависят от температуры. К ним относятся скорость потока, теплоемкости, коэффициенты изотерм адсорбции, коэффициенты уравнений массо- и теплопередачи. Поэтому базовая система (М5) обычно дополняется соотношениями, учитывающими зависимости параметров от температуры. Полная система, описывающая адиабатическую адсорбцию, приобретает громоздкую форму. Ее аналитическое решение невозможно. В литературе представлены немногочисленные лримеры численных решений модели (М5).

    Феноменология процесса. Качественные особенности протекания адиабатических процессов рассмотрены в работах двух групп исследователей: Тодеса-Лезина и Пана-Басмаджиана. Эти работы и положены в основу приведенного ниже обсуждения. Авторы выделяют два предельных (идеализированных) режима переноса температурного и концентрационного фронтов в слое: режим одиночной тепловой волны и режим комбинированных волн. Выходные кривые для них приведены на рис. 1. 18 и 1. 19.

    Рис. 1. 18. Выходные кривые адиабатической адсорбции для режима одиночной тепловой волны: 1 – температурная кривая, 2 – концентрационная кривая.

 

    Рис. 1. 19. Выходные кривые адиабатической адсорбции для режима комбинированных волн: 1 – температурная кривая, 2 – концентрационная кривая.

 

    Кривые на рисунках разбиты на интервалы для того, чтобы облегчить их обсуждение. Итак, на участке ОА рис. 1. 18 температура потока и концентрация примеси в нем за слоем длиною L равны начальным значениям этих переменных. Изменения температуры и концентрации, обусловленные адсорбцией, происходят внутри слоя и пока не проявляются на выходе из него. В точке А из слоя начинает выходить поток с повышенной температурой; концентрация продолжает оставаться неизменной и равной начальной. В точке В, когда температура достигает максимального значения (Т_max ), на выходе из слоя появляется концентрационная точка отвечающая более высокому, чем начальное, содержанию адсорбата в потоке. Таким образом, в течение времени, пропорционального протяженности участка АВ, из слоя выходит «горячий» и чистый поток. Тепловой фронт обогнал фронт концентрационный, что и дало основания назвать такой режим режимом одиночной тепловой волны.

    Концентрация примеси за слоем продолжает нарастать, Но скорость адсорбции уменьшилась, приход тепла от адсорбции не компенсирует его вынос с потоком и подъем температуры сменяется ее падением. Начало падения, которое происходит из-за поступления в слой сравнительно холодного очищаемого газа, обозначено на рисунке точкой С. После того, как адсорбция примеси в слое завершилась, на выходе из него появилась концентрационная точка, отвечающая содержанию примеси в исходном потоке (Со). Температура потока к этому моменту времени достигла значения, характерного для газа, поступающего на очистку. Завершению процессов тепло- и массообмена отвечает точка Д.

    Кривые распределения температур и концентраций в слое есть некоторое «обращение» выходных кривых внутрь слоя. Для режима одиночной тепловой волны и некоторого времени t кривые распределения приведены на рис. 1. 20.

 

    Рис. 1. 20. Кривые распределения температур (1) и концентраций (2) в слое адсорбента (t < t_A ) для режима одиночной тепловой волны

 

       Рассмотрим выходные кривые на рис. 1. 19. На участке ОА изменения температуры и концентрации отсутствуют: они происходят внутри слоя адсорбента. В точке А на выходе из слоя почти одновременно появляются температура и концентрация, отличные от начальных значений этих параметров. В точке В температура достигает максимального значения (Т_max )  а концентрация приближается к значению (С’), промежуточному между содержанием адсорбата в исходном потоке и его начальным содержанием в адсорбенте. Далее, вплоть до точки С значения концентрации и температуры почти постоянны. Концентрация и температура достигают исходного уровня в точке Д. Из-за одновременного появления за слоем температурной и концентрационной волн режим называют комбинированным. На рис 1. 21 приведены кривые распределения температур и концентраций в слое.

    Подчеркнем особенности режимов. В режиме одиночной тепловой волны, начиная с некоторого момента времени, когда адсорбция в слое еще не завершена, тепло адсорбции начинает выноситься из слоя. В режиме комбинированных волн тепло адсорбции не выносится из слоя, а аккумулируется в нем вплоть до почти полного завершения адсорбции.

 

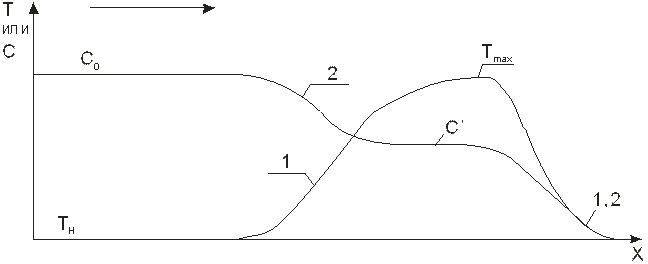
    Рис. 1. 21. Кривые распределения температур (1) и концентраций (2) в момент времени t < t_A.  в режиме комбинированных волн.

 

    Причины существования двух режимов лежат в соотношениях между скоростями движения тепловой и концентрационной волн. Выражения для них были получены в разделах 1. 4. 2 и 1. 4. 3 для режимов более простых, чем адиабатический. Они повторно записаны ниже:

 

U_c = WCo/(X*o + Co),                     (1. 28)

 

U_t = Wh/(H + h).                              (1. 24)

 

    Очевидно, что в принципе возможны две ситуации: U_с < U_t  и U_c ≥ U_t. Так как источником тепла в рассматриваемой задаче является адсорбция, тепло выделяется тогда и там, где она происходит. Поэтому выполнение первого из неравенств означает, что тепло, выделяющееся в зоне протекания адсорбции, потоком газа выносится из этой зоны, тепловая волна обгоняет волну концентрационную и адсорбция идет на адсорбенте, охлажденном потоком.

    Приближенное значение Т_max находят в предположении, что фронты сохраняют свою конфигурацию. Для этого случая можно записать:

 

∆ H(X*₀. ∆ l. S) = ∆ l. S. H. ∆ T + ∆ l. S. h. ∆ T + WS. h ∆ t. ∆ T,

 

где ∆ l – протяженность участка слоя, на который сместился концентрационный фронт за время ∆ t; ∆ T = T_max  - T. Выражение в левой части уравнения – количество тепла, которое выделилось в этот инкременте слоя за это время. Второе и третье слагаемые правой части отвечают количеству тепла, пошедшему на нагрев инкремента слоя и находящейся в нем объемной фазы, последнее слагаемое соответствует количеству тепла на нагрев потока, пропущенному за время ∆ t и вынесенному за пределы инкремента ∆ l.

Преобразуем выражение в следующую форму:       

 

∆ H(X*₀ (∆ l/∆ t)) = ∆ T[(H + h) (∆ l/∆ t) + Wh]

 

Учтем, что ∆ l/∆ t = U_c, a U_c /W = Со/(Х*о + Со). После подстановок получаем

 

T_max = T₀ + ∆ H. X*o/[H + h +h(X*o + Co)/Co]                     (1. 30).

 

    Уравнение (1. 30) вместе с уравнениями (1. 24) и (1. 28) являются основными для приближенного описания режима одиночной тепловой волны.

    Пусть выполняется неравенство U_с > U_t. Тепловой фронт, казалось бы, должен отставать от фронта концентрационного. Но тепло выделяется при адсорбции и головной участок теплового фронта не может отстать от фронта концентрационного. Он движется вместе с ним: с несобственной скоростью, а со скоростью движения концентрационной волны. Таким образом, для этого режима имеем:

 

U_t1 = U_c = WC’ /(X*_{С = С’} + C’),                      (1. 31).

 

где U_t1 – скорость движения головного участка теплового фронта. Тыловой участок теплового фронта движется с собственной скоростью (U_t2), задаваемой уравнением (1. 24) Между участками образуется расширяющаяся зона нагретого сорбента, протяженность которого к моменту времени t равна t(U_t1 - U_t2). Приход тепла в этой зоне равен ∆ Н. Х*_С’, расход – (H + h)∆ Т. Отсюда

∆ Т = ∆ H. X*_С'/(Н + h)                              (1. 32)

        

       Решение уравнения (1. 32) совместно с изотермами адсорбции позволяет определить максимальную температуру в зоне между фронтами, величину адсорбции и концентрации.

Приведенные выше уравнения для скоростей движения волн отвечали их центрам тяжести. На основании этих скоростей вычисляются предельные (максимальные) возможности слоя. Однако из-за потребности в выносе тепла кривые распределения в адиабатической адсорбции имеют более значительную протяженность, чем в адсорбции изотермической. Поэтому различия в практической и предельной возможностях в адиабатической динамике велики и нет способа рассчитать реальную очищающую способность слоя, кроме математического моделирования.

 

⇐ Предыдущая3456789101112Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: