 |
Геометрический способ определения равнодействующей плоской системы сходящихся сил.
|
|
|
|
Плоская система сходящихся сил – это такая система сил, в которой линии действия всех сил лежат в одной плоскости и все пересекаются в одной точке.
Любую плоскую систему сходящихся сил можно привести к одной силе, которая называется равнодействующей силой. Эта равнодействующая сила равна векторной сумме всех сил, входящих в систему.
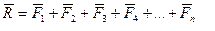 или сокращённо
или сокращённо

Проекции силы на оси координат.
Проекция силы на координатную ось – это отрезок оси, расположенный между двумя перпендикулярами, опущенными на ось из начала и конца вектора силы.
Если между линией действия силы F и осью х угол будет равен значению α, то проекции силы F на координатные оси будут равны:
FХ = F · cos α
FУ = F · sin α

Если вектор силы параллелен оси, то он проецируется на эту ось в натуральную величину, а если вектор силы перпендикулярен оси, то его проекция на эту ось равна нулю.
Аналитический способ определения равнодействующей плоской системы сходящихся сил.
Значение равнодействующей силы у плоской системы сходящихся сил аналитически вычисляется следующим образом:
1. Вычисляется сумма проекций всех сил системы на координатные оси х,у:
Rх = Σ Fiх
Rу = Σ Fiу
2. Вычисляется значение равнодействующей силы:

Условие равновесия плоской системы сходящихся сил.
1. Геометрическое условие равновесия – равнодействующая сила должна равняться нулю:
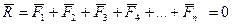
Сокращенно можно записать

2. Аналитическое условие равновесия – алгебраическая сумма проекций всех сил системы на координатные оси должна равняться нулю:
Σ Fiх = 0; F1X + F2X + F3X + … + Fnx = 0
Σ Fiу = 0; F1У + F2У + F3У + … + Fnу = 0
Названные выше уравнения называются уравнениями равновесия для плоской системы сходящихся сил.
|
|
|
Основная литература: 1;2
Дополнительная литература: 1;3
Контрольные вопросы.
1. Дайте определение плоской системы сходящихся сил.
2. Дайте определение равнодействующей силы.
3. Каким образом геометрически вычисляется равнодействующая сила плоской системы сходящихся сил?
4. Что такое проекция силы на оси координат?
5. Каким образом вычисляются проекции силы на оси координат?
6. Каким образом аналитически вычисляется равнодействующая сила плоской системы сходящихся сил?
7. Назовите условия равновесия плоской системы сходящихся сил.
Лекция №4.
Цели занятия:
Рассмотреть распределённую нагрузку, где встречается распределённая нагрузка, каким образом рассчитываются конструкции при действии на них распределённых нагрузок.
План занятия:
1. Понятие распределённой нагрузки.
2. Примеры, где встречается распределённая нагрузка.
3. Равномерно распределённая нагрузка.
4. Приведение распределённой нагрузки к одной общей силе.
5. Неравномерно распределённые нагрузки.
Плоская система произвольно расположенных сил.
Распределённые нагрузки.
В природе часто встречаются силы, приложенные по поверхности тела. Такие силы называются распределёнными нагрузками.
Пространственные распределённые нагрузки характеризуются интенсивностью p (Н/м2), на плоскости распределённые нагрузки характеризуются интенсивностью q (Н/м).
Интенсивность пространственной распределённой нагрузки можно перевести в интенсивность на плоскости по формуле
q = р·b
где b – ширина действия распределённой нагрузки.
Распределённые нагрузки бывают равномерно распределёнными и неравномерно распределёнными.
Равномерно распределённые нагрузки имеют постоянную интенсивность, неравномерно распределённые нагрузки имеют не постоянную интенсивность.
Рассмотрим равномерно распределённую нагрузку.
|
|
|
При расчётах распределённую нагрузку заменяют равнодействующей силой Q, которая будет приложена в середине участка, на котором действует распределённая нагрузка.
Q = q·l
где l – длина действия распределённой нагрузки.
Рассмотрим неравномерно распределённые нагрузки.
1. Треугольная распределённая нагрузка.
У треугольной распределённой нагрузки равнодействующая сила Q равна:
Q = qmax·l / 2
2. Трапецеидальная распределённая нагрузка.
При расчетах трапецеидальную распределённую нагрузку распределяют на две распределённые нагрузки: прямоугольную и треугольную. Прямоугольную распределённую нагрузку заменяют равнодействующей силой Q1, а треугольную распределённую нагрузку заменяют равнодействующей силой Q2, которые будут равны:
Q1 = qmin·l
Q2 = (qmax - qmin) ·l / 2
Методом разделения сложной фигуры на две и более простые можно вычислить равнодействующие силы у других неравномерно распределённых нагрузок.
Существуют также криволинейные неравномерно распределённые нагрузки. Равнодействующие силы у таких распределённых нагрузок и точки их приложения вычисляются методами дифференциального и интегрального исчисления.
Основная литература: 1;2
Дополнительная литература: 1;3
Контрольные вопросы.
1. Что такое распределённая нагрузка?
2. Чем характеризуется распределённая нагрузка?
3. Какие бывают распределённые нагрузки?
4. Что делают с распределёнными нагрузками при расчётах?
Лекция №5.
Цели занятия:
1. Рассмотреть понятие момента силы относительно точки, где в технике применяется момент силы.
2. Рассмотреть понятие пары сил, где в технике применяется пара сил.
План занятия:
1. Момент силы относительно точки.
2. Пара сил.
3. Момент пары.
4. Теорема о сложении пар.
5. Условие равновесия плоской системы пар.
6. Основные свойства пары.
|
|
|


