 |
Преобразование вращательных движений.
|
|
|
|
Преобразование вращательных движений осуществляется механизмами, которые называются механическими передачами. С помощью механических передач осуществляется передача вращательного движения от источника движения (ведущего вала) к приёмнику движения (ведомому валу).
Виды механических передач: зубчатые, червячные, фрикционные, ремённые, цепные.
Механические передачи характеризуются передаточным отношением, которое показывает, во сколько раз уменьшается частота вращения в передаче.
U – передаточное отношение
U12 = (ω1 /ω2 ) = (n1 /n2 )
где - ω1 - угловая скорость ведущего вала
ω2 - угловая скорость ведомого вала
Если U ˃ 1, передача понижающая (редуктор)
Если U ˂ 1, передача повышающая (мультипликатор)
Если U = 1, угловая скорость в передаче не изменяется
Основная литература: 1;2
Дополнительная литература: 1;3
Контрольные вопросы.
1. Какие бывают виды простейших движений твёрдого тела?
2. Что такое поступательное движение?
3. Что такое вращательное движение?
4. Чем характеризуется вращательное движение?
5. Что такое угловая скорость, как она вычисляется?
6. По какой формуле частота вращения переводится в угловую скорость?
7. Назовите формулу Эйлера.
8. Что такое угловое ускорение, каким образом оно вычисляется?
9. Каким образом вычисляется ускорение точки вращающегося тела?
10. Каким образом осуществляется преобразование вращательного движения?
11. Чем характеризуются механические передачи?
Лекция №18,19.
Цели занятия: Рассмотреть сложное движение точки, из каких видов движений состоит сложное движение, привести примеры, где в технике встречается сложное движение.
План занятия:
1. Понятие о сложном движении точки.
|
|
|
2. Определение скорости точки при сложном движении.
3. Определение ускорения точки при сложном движении.
Сложное движение точки.
Сложное движение точки – это движение точки относительно сразу двух систем отсчёта, первая из которых условно считается неподвижной, а вторая движется относительно первой.
Движение точки относительно подвижной системы отсчёта называется относительным. Движение подвижной системы отсчёта относительно неподвижной называется переносным. Движение точки относительно неподвижной системы отсчёта называется сложным.
Например, человек идёт по движущемуся автобусу. Движение человека по автобусу будет относительным движением, движение автобуса относительно земли будет переносным, а движение человека относительно земли будет сложным.
Скорость точки при сложном движении относительно неподвижной системы координат называется абсолютной.
Теорема о сложении скоростей: абсолютная скорость точки при сложном движении равна векторной сумме относительной и переносной скоростей.

где VАБС – абсолютная скорость точки
VОТН– относительная скорость точки
VПЕР – переносная скорость точки
Аналитически абсолютную скорость можно определить по формуле из теоремы косинусов:
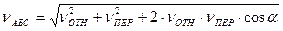
где α – угол между векторами скоростей VОТН и VПЕР
При сложном движении точка будет иметь относительное, переносное и кориолисово ускорения.
Кориолисово ускорение – это величина, характеризующая изменение относительной скорости точки при переносном движении и переносной скорости точки при её относительном движении.
Кориолисово ускорение обозначается aКОР и определяется по следующим формулам.
В векторной форме:

Аналитически:
a КОР = 2· | ω | · | VОТН | · sin α
где α – угол между вектором скорости VОТН и осью вращения.
Направление кориолисова ускорения определяется по правилу Н. Е. Жуковского: вектор VОТН проецируется на плоскость, перпендикулярную оси вращения и далее эта проекция поворачивается на 900 в сторону направления угловой скорости ω.
|
|
|
Абсолютное ускорение точки равно векторной сумме относительного, переносного и кориолисова ускорений.
 или в более развёрнутом виде
или в более развёрнутом виде

Аналитически абсолютное ускорение вычисляется в следующей последовательности:
1. Все ускорения проецируются на координатные оси x,y,z.
2. Определяются значения проекций ускорений на координатные оси x,y,z.
3. Вычисляется алгебраическая сумма проекций всех ускорений на координатные оси x,y,z.
4. Вычисляется абсолютное ускорение точки по формуле

Основная литература: 1;2
Дополнительная литература: 1;3
Контрольные вопросы.
1. Дайте определение сложному движению точки.
2. Из каких движений состоит сложное движение точки?
3. Каким образом вычисляется скорость при сложном движении?
4. Дайте определение кориолисовому ускорению.
5. Каким образом вычисляется ускорение при сложном движении?
Лекция №20.
Цели занятия: Рассмотреть плоскопараллельное движение твёрдого тела, привести примеры, где в технике встречается данный вид движения.
План занятия:
1. Понятие плоскопараллельного движения твёрдого тела.
2. Метод мгновенных центров скоростей.
|
|
|


