 |
Метод кинетостатики. Принцип Даламбера.
|
|
|
|
Материальная точка массой m движется с ускорением a под действием системы сил, равнодействующая которых равна F.
Применим основное уравнение динамики:
F = m · a
Запишем данное уравнение в следующем виде:
F + (- m · a) = 0
Выражение в скобках называется силой инерции, обозначается FИН
FИН = - m · a
Знак минус означает, что сила инерции направлена в сторону, противоположную направлению ускорения.
Теперь можно записать:
F + FИН = 0
Данное равенство является математическим выражением принципа Даламбера. Его можно рассматривать, как уравнение равновесия материальной точки. Это равенство хотя и названо уравнением равновесия, в действительности является видоизменённым уравнением движения материальной точки.
Принцип Даламбера: активные и реактивные силы, действующие на материальную точку, вместе с силами инерции образуют систему взаимно уравновешенных сил, удовлетворяющую всем условиям равновесия.
Сила инерции приложена к рассматриваемой материальной точке условно, но для связи, вызывающей ускорение, она в определённом смысле является реальной.
Рассмотрим пример. К телу, лежащему на горизонтальной плоскости, привязана нить, способная выдержать силу тяжести G этого тела. Если к нити приложить силу F статически (постепенно), то тело поднимется вверх и нить не оборвётся; если силу F приложить динамически (резким рывком), то нить оборвётся.
Это явление объясняется следующим образом. Чтобы поднять тело, нужно сообщить ему какое – то ускорение a. Для определения величины натяжения нити применим принцип Даламбера. При поднятии тела на данную систему действуют следующие силы: вверх действует сила F, которая поднимает тело, вниз действует сила тяжести тела G и сила инерции FИН (ускорение будет направлено вверх, следовательно сила инерции будет направлена вниз).
|
|
|
Составим уравнение равновесия:
Σ Fix = 0; F – G – FИН = 0
Отсюда получаем:
F = G + FИН = G + m · a
Если к нити приложить силу F статически, то значение ускорения будет небольшим и сила инерции, увеличивающая натяжение нити, небольшая; если силу F приложить резким рывком, то ускорение будет значительным, и значение силы инерции будет большим.
Силы инерции в криволинейном движении.
При криволинейном движении точки полное ускорение раскладывается на два ускорения: нормальное и касательное, следовательно сила инерции также разложится на две силы: на нормальную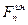 
и касательную 
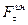, которые будут направлены в стороны, противоположные соответствующим ускорениям.
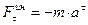
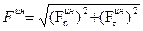
Основная литература: 1;2
Дополнительная литература: 2;3
Контрольные вопросы.
1. Сформулируйте принцип Даламбера.
2. Каким образом вычисляется и в какую сторону направлена сила инерции?
3. Каким образом вычисляются силы инерции при криволинейном движении точки?
Лекция №25,26.
Цели занятия:
1. Рассмотреть понятие работа, каким образом вычисляется работа при различных случаях в технике, привести примеры.
2. Рассмотреть понятие мощность, каким образом вычисляется мощность при различных случаях в технике, привести примеры.
План занятия:
1. Понятие работа.
2. Работа постоянной силы на прямолинейном участке пути.
3. Работа переменной силы на криволинейном участке пути.
4. Работа равнодействующей.
5. Работа силы тяжести.
6. Работа при вращательном движении.
7. Мощность.
Работа.
При движении тела под действием силы F тело пройдёт какой – то путь S. При этом будет совершена какая – то работа.
А – работа
В общем случае работа вычисляется как произведение модуля силы на пройденный путь:
А = F · S (Н · м = Дж)
|
|
|
Однако есть случаи, когда значение работы вычисляется по другим формулам. Рассмотрим эти случаи.
1. Работа постоянной силы на прямолинейном участке пути.
А = F · S · cos α
где α – угол между линией действия силы и направлением перемещения.
Если α = 00 , тогда А = F · S, т.к. cos 00 = 1
Если α = 900 , тогда А = 0, т.к. cos 900 = 0
Если α = 1800 , тогда А = - F · S, т.к. cos 1800 = - 1
2. Работа переменной силы на криволинейном участке пути.
S
A = ʃ F · cos α dS
где α – угол между линией действия силы F и касательной, проведённой к траектории движения тела.
3. На тело действует система постоянных сил, равнодействующая которых равна R.
В этом случае применяется теорема о работе равнодействующей: работа равнодействующей силы на каком – то участке пути равна алгебраической сумме работ сил данной системы на том же участке пути.
Это значит, что от действия силы F1 была совершена работа А1, от действия силы F2 была совершена работа А2 и т.д., от действия силы Fn была совершена работа Аn.
От действия равнодействующей силы R была совершена работа А.
Можно записать:
А = А1 + А2 + А3 + … + Аn или сокращённо
А = Σ Аi
4. Тело перемещается под действием силы тяжести.
В этом случае применяется теорема о работе силы тяжести: работа силы тяжести не зависит от вида траектории и равна произведению модуля силы на вертикальное перемещение тела.
А = G · h
где h – вертикальное перемещение тела.
5. Тело совершает вращательное движение под действием постоянной силы.
При этом также будет совершаться какая – то работа, которая вычисляется следующим образом.
Рассмотрим тело, которое под действием постоянной силы F повернулось на угол φ. Сила F действует на тело в точке В.
Спроецируем силу F на касательную, проведённую к траектории движения точки В, получим силу Ft. Эта сила относительно оси вращения создаст момент, который называется вращающимся моментом и обозначается М.
М = Ft · r (Н · м)
где r – кратчайшее расстояние от силы Ft до оси вращения.
Работа будет равна:
А = Т · φ (Н · м · рад = Н · м · 1 = Н · м = Дж)
Мощность.
Мощность – это работа, совершённая в единицу времени.
Р – мощность
Мощность определяется по формуле:
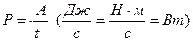
При поступательном движении мощность можно определить по формуле:
|
|
|
где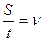 
; тогда
Р = F · V 
При вращательном движении мощность можно определить по формуле:
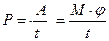
где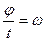 
; тогда
Р = М · ω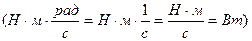 
Основная литература: 1;2
Дополнительная литература: 2;3
Контрольные вопросы.
1. Что такое работа?
2. По какой формуле вычисляется работа в общем случае?
3. Каким образом вычисляется работа постоянной силы на прямолинейном участке пути?
4. Каким образом вычисляется работа переменной силы на криволинейном участке пути?
5. Сформулируйте теорему о работе равнодействующей.
6. По каким причинам совершается работа силы тяжести, каким образом она вычисляется?
7. Каким образом вычисляется работа при вращательном движении.
8. Что такое мощность, по какой формуле вычисляется мощность?
9. По какой формуле вычисляется мощность при поступательном движении?
10. По какой формуле вычисляется мощность при вращательном движении?
Лекция №27.
Цели занятия: Рассмотреть количество движения тела, теорему об изменении количества движения.
План занятия:
1. Количество движения тела.
2. Импульс силы.
3. Теорема об изменении количества движения.
|
|
|
