 |
Элементарные тригонометрические уравнения
|
|
|
|
Тригонометрические уравнения и неравенства
Курсовая работа
Исполнитель:
студент группы М-51
С.М. Горский
Научный руководительк.ф.- м.н.,
старший преподаватель
В.Г. Сафонов
Гомель 2008
Оглавление
ВВЕДЕНИЕ
ОСНОВНЫЕ МЕТОДЫ РЕШЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
Элементарные тригонометрические уравнения
Введение вспомогательного аргумента
Схема решения тригонометрических уравнений
Преобразование и объединение групп общих решений тригонометрических уравнений
Разложение на множители
Решение уравнений преобразованием произведения тригонометрических функций в сумму
Решение уравнений с применением формул понижения степени
Решение уравнений с применением формул тройного аргумента
Равенство одноименных тригонометрических функций
Домножение на некоторую тригонометрическую функцию
Сведение тригонометрических уравнений к алгебраическим
НЕСТАНДАРТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ
Использование ограниченности функций
Функциональные методы решения тригонометрических и комбинированных уравнений
Решение с исследованием функции
ТРИГОНОМЕТРИЧЕСКИЕ НЕРАВЕНСТВА
Решение тригонометрических неравенств с помощью единичной окружности
Решение тригонометрических неравенств графическим методом
ОТБОР КОРНЕЙ
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
ЗАКЛЮЧЕНИЕ
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
ВВЕДЕНИЕ
В древности тригонометрия возникла в связи с потребностями астрономии, землемерия и строительного дела, то есть носила чисто геометрический характер и представляла главным образом <<исчисление хорд>>. Со временем в нее начали вкрапляться некоторые аналитические моменты. В первой половине 18-го века произошел резкий перелом, после чего тригонометрия приняла новое направление и сместилась в сторону математического анализа. Именно в это время тригонометрические зависимости стали рассматриваться как функции.
|
|
|
Тригонометрические уравнения одна из самых сложных тем в школьном курсе математики. Тригонометрические уравнения возникают при решении задач по планиметрии, стереометрии, астрономии, физики и в других областях. Тригонометрические уравнения и неравенства из года в год встречаются среди заданий централизованного тестирования.
Самое важное отличие тригонометрических уравнений от алгебраических состоит в том, что в алгебраических уравнениях конечное число корней, а в тригонометрических --- бесконечное, что сильно усложняет отбор корней. Еще одной спецификой тригонометрических уравнений является неединственность формы записи ответа.
Данная дипломная работа посвящена методам решения тригонометрических уравнений и неравенств.
Дипломная работа состоит из 6 разделов.
В первом разделе приведены основные теоретические сведения: определение и свойства тригонометрических и обратных тригонометрических функций; таблица значений тригонометрических функций для некоторых аргументов; выражение тригонометрических функций через другие тригонометрических функции, что очень важно для преобразования тригонометрических выражений, в особенности содержащих обратные тригонометрические функции; кроме основных тригонометрических формул, хорошо известных из школьного курса, приведены формулы упрощающие выражения, содержащие обратные тригонометрические функции.
Во втором разделе изложены основные методы решения тригонометрических уравнений. Рассмотрены решение элементарных тригонометрических уравнений, метод разложения на множители, методы сведения тригонометрических уравнений к алгебраическим. Ввиду того, что решения тригонометрических уравнений можно записать несколькими способами, и вид этих решений не позволяет сразу установить, являются ли эти решения одинаковыми или различными, что может <<сбить с толку>> при решении тестов, рассмотрена общая схема решения тригонометрических уравнений и подробно рассмотрено преобразование групп общих решений тригонометрических уравнений.
|
|
|
В третьем разделе рассматриваются нестандартные тригонометрические уравнения, решения которых основано на функциональном подходе.
В четвертом разделе рассматриваются тригонометрические неравенства. Подробно рассмотрены методы решения элементарных тригонометрических неравенств, как на единичной окружности, так и графическим методом. Описан процесс решения неэлементарных тригонометрических неравенств через элементарные неравенства и уже хорошо известный школьникам метод интервалов.
В пятом разделе представлены наиболее сложные задания: когда необходимо не только решить тригонометрическое уравнение, но и из найденных корней отобрать корни, удовлетворяющие какому-нибудь условию. В данном разделе приведены решения типичных заданий на отбор корней. Приведены необходимые теоретических сведения для отбора корней: разбиение множества целых чисел на непересекающиеся подмножества, решение уравнений в целых числах (диафантовых).
В шестом разделе представлены задачи для самостоятельного решения, оформленные в виде теста. В 20 заданиях теста приведены наиболее сложные задания, которые могут встретиться на централизованном тестировании.
ОСНОВНЫЕ МЕТОДЫ РЕШЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
Элементарные тригонометрические уравнения
Элементарные тригонометрические уравнения --- это уравнения вида 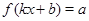 , где
, где 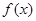 --- одна из тригонометрических функций:
--- одна из тригонометрических функций:  ,
,  ,
,  ,
,  .
.
Элементарные тригонометрические уравнения имеют бесконечно много корней. Например, уравнению  удовлетворяют следующие значения:
удовлетворяют следующие значения:  ,
, 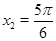 ,
,  ,
,  и т. д. Общая формула по которой находятся все корни уравнения
и т. д. Общая формула по которой находятся все корни уравнения  , где
, где  , такова:
, такова:

Здесь  может принимать любые целые значения, каждому из них соответствует определенный корень уравнения; в этой формуле (равно как и в других формулах, по которым решаются элементарные тригонометрические уравнения)
может принимать любые целые значения, каждому из них соответствует определенный корень уравнения; в этой формуле (равно как и в других формулах, по которым решаются элементарные тригонометрические уравнения)  называют параметром. Записывают обычно
называют параметром. Записывают обычно  , подчеркивая тем самым, что параметр
, подчеркивая тем самым, что параметр  принимать любые целые значения.
принимать любые целые значения.
|
|
|
Решения уравнения  , где
, где  , находятся по формуле
, находятся по формуле

Уравнение  решается применяя формулу
решается применяя формулу

а уравнение  --- по формуле
--- по формуле
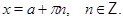
Особо отметим некоторые частные случаи элементраных тригонометрических уравнений, когда решение может быть записано без применения общих формул:





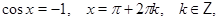






При решении тригонометрических уравнений важную роль играет период тригонометрических функций. Поэтому приведем две полезные теоремы:
Теорема Если  --- основной период функции
--- основной период функции 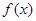 , то число
, то число  является основным периодом функции
является основным периодом функции  .
.
Периоды функций  и
и  называются соизмеримыми, если существуют натуральные числа
называются соизмеримыми, если существуют натуральные числа  и
и  , что
, что  .
.
Теорема Если периодические функции  и
и  , имеют соизмеримые
, имеют соизмеримые 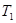 и
и  , то они имеют общий период
, то они имеют общий период  , который является периодом функций
, который является периодом функций  ,
,  ,
,  .
.
В теореме говорится о том, что  является периодом функции
является периодом функции 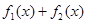 ,
,  ,
,  , и не обязательно является основным периодом. Например, основной период функций
, и не обязательно является основным периодом. Например, основной период функций  и
и  ---
---  , а основной период их произведения ---
, а основной период их произведения ---  .
.
|
|
|


