 |
Решение уравнений с примененнием формул тройного аргумента
|
|
|
|
Пример Решить уравнение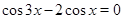 
.
Решение. Применим формулу, получим уравнение
Ответ. 
; 
.
Пример Решить уравнение 
.
Решение. Применим формулы понижения степени получим: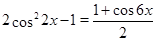 
. Применяя получаем:
.
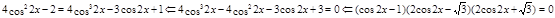Ответ. 
; 
.
Равенство одноименных тригонометрических функций
Пример Решить уравнение 
.
Решение.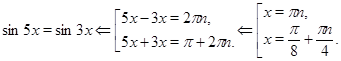 
Ответ. , 
.
Пример Решить уравнение 
.
Решение. Преобразуем уравнение.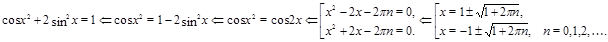 
Ответ. 
.
Пример Известно, что 
и 
удовлетворяют уравнению
Найти сумму 
.
Решение. Из уравнения следует, что
Ответ. 
.
Домножение на некоторую тригонометрическую функцию
Рассмотрим суммы вида
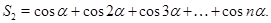
Данные суммы можно преобразовать в произведение, домножив и разделив их на 
, тогда получим
Указанный прием может быть использован при решении некоторых тригонометрических уравнений, однако следует иметь в виду, что в результате возможно появление посторонних корней. Приведем обобщение данных формул:
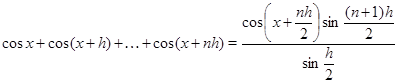
Пример Решить уравнение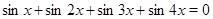 
.
Решение. Видно, что множество 
является решением исходного уравнения. Поэтому умножение левой и правой части уравнения на 
не приведет к появлению лишних корней.
Имеем 
.
Ответ. 
; 
.
Пример Решить уравнение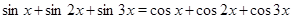 
.
Решение. Домножим левую и правую части уравнения на 
и применив формулы преобразования произведения тригонометрических функций в сумму, пролучим
Это уравнение равносильно совокупности двух уравнений 
и 
, откуда 
и 
.
Так как корни уравнения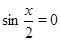 
не являются корнями уравнения, то из полученных множеств решений следует исключить 
. Значит во множестве нужно исключить 
.
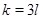Ответ. и 
, 
.
Пример Решить уравнение 
.
|
|
|
Решение. Преобразуем выражение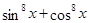 
:
Уравнение запишется в виде:
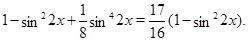
Принимая 
, получаем 
. 
, 
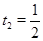. Следовательно
Ответ. 
.
Сведение тригонометрических уравнений к алгебраическим
Сводящиеся к квадратным
Если уравнение имеет вид
то замена 
приводит его к квадратному, поскольку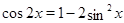 
() и.
Если вместо слагаемого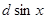 
будет 
, то нужная замена будет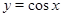 
.
Уравнение
сводится к квадратному уравнению
представлением 
как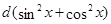 
. Легко проверить, что 
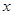при которых 
, не являются корнями уравнения, и, сделав замену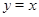 
, уравнение сводится к квадратному.
Пример Решить уравнение 
.
Решение. Перенесем 
в левую часть, заменим ее на 
, 
и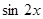 
выразим через 
и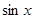 
.
После упрощений получим: 
. Разделим почленно на 
, сделаем замену 
:
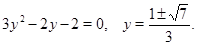
Возвращаясь к 
, найдем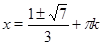 
.
Уравнения, однородные относительно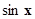 
, 
Рассмотрим уравнение вида
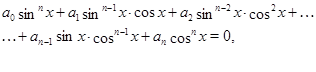
где 
, 
, 
,..., 
, 
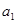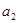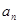--- действительные числа. В каждом слагаемом левой части уравнения степени одночленов равны 
, т. е. сумма степеней синуса и косинуса одна и та же и равна 
. Такое уравнение называется однородным относительно 
и , а число называется показателем однородности.
Ясно, что если 
, то уравнение примет вид:
решениями которого являются значения 
, при которых 
, т. е. числа 
, 
. Второе уравнение, записанное в скобках также является однородным, но степени на 1 ниже.
Если же 
, то эти числа не являются корнями уравнения.
При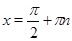 
получим: 
, 
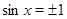и левая часть уравнения (1) принимает значение 
.
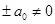Итак, при , 
и 
, поэтому можно разделить обе части уравнения на 
. В результате получаем уравнение:
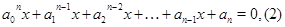
которое, подстановкой 
легко сводится к алгебраическому:
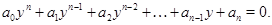
Однородные уравнения с показателем однородности 1. При 
имеем уравнение 
.
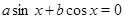Если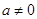 
, то это уравнение равносильно уравнению 
, 
, откуда 
, .
Пример Решите уравнение 
.
|
|
|
Решение. Это уравнение однородное первой степени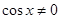 
. Разделим обе его части на получим: 
, 
, 
, 
.
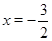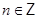Ответ. 
.
Пример При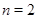 
получим однородное уравнение вида
Решение.
Если 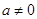, тогда разделим обе части уравнения на 
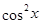, получим уравнение 
, которое подстановкой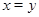 
легко приводится к квадратному: 
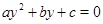. Если 
, то уравнение имеет действительные корни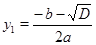 
, 
. Исходное уравнение будет иметь две группы решений: 
, 
, 
.
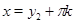Если 
, то уравнение не имеет решений.
Пример Решите уравнение 
.
Решение. Это уравнение однородное второй степени. Разделим обе чести уравнения на 
, получим: 
. Пусть , тогда 
, 
, 
. 
, 
, ; 
, 
, 
.
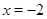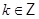Ответ. 
.
К уравнению вида сводится уравнение
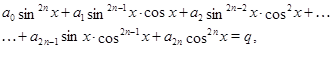
Для этого достаточно воспользоваться тождеством 
В частности, уравнение 
сводится к однородному, если заменить на 
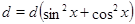, тогда получим равносильное уравнение: 
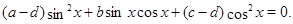
Пример Решите уравнение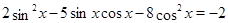 
.
Решение. Преобразуем уравнение к однородному:
Разделим обе части уравнения на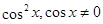 
, получим уравнение:
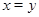Пусть , тогда приходим к квадратному уравнению: 
, 
, 
, 
, 
.
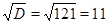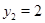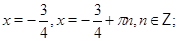
Ответ.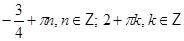 
.
Пример Решите уравнение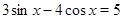 
.
Решение. Возведем обе части уравнения в квадрат, учитывая, что они имеют положительные значения: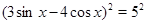 
, 
,
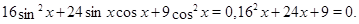
Пусть 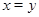, тогда получим 
, 
, 
.
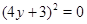Ответ. 
.
Уравнения, решаемые с помощью тождеств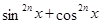 
Полезно знать следующие формулы:
Пример Решить уравнение 
.
Решение. Используя, получаем
Ответ. 
Предлагаем не сами формулы, а способ их вывода:
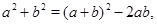
следовательно,
.
Аналогично,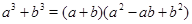 
.
Пример Решить уравнение 
.
Решение. Преобразуем выражение :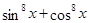
.
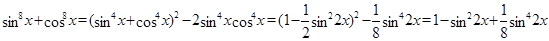Уравнение запишется в виде:
Принимая 
, получаем 
. , 
. Следовательно
Ответ.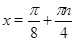 
.
|
|
|
