 |
Функциональные методы решения тригонометрических и комбинированных уравнений
|
|
|
|
Не всякое уравнение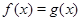 
в результате преобразований может быть сведено к уравнению того или иного стандартного вида, для которого существует определенный метод решения. В таких случаях оказывается полезным использовать такие свойства функций 
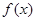и 
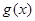, как монотонность, ограниченность, четность, периодичность и др. Так, если одна из функций убывает, а вторая возрастает на промежутке 
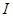, то при наличии у уравнения 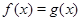корня на этом промежутке, этот корень единственный, и тогда его, например, можно найти подбором. Если же функция 
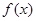ограничена сверху, причем 
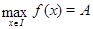, а функция 
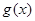ограничена снизу, причем 
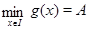, то уравнение 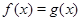равносильно системе уравнений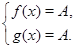 
Пример Решить уравнение
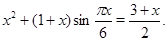
Решение. Преобразуем исходное уравнение к виду
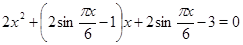
и решим его как квадратное относительно 
. Тогда получим,
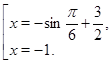
Решим первое уравнение совокупности. Учтя ограниченность функции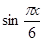 
, приходим к выводу, что уравнение может иметь корень только на отрезке 
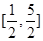. На этом промежутке функция 
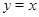возрастает, а функция 
убывает. Следовательно, если это уравнение имеет корень, то он единственный. Подбором находим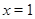 
.
Ответ.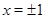 
.
Пример Решить уравнение
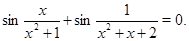
Решение. Пусть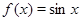 
, 
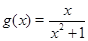и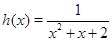 
, тогда исходное уравнение можно записать в виде функционального уравнения 
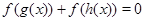. Поскольку 
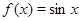функция нечетная, то 
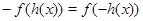. В таком случае получаем уравнение 
.
Так как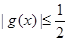 
, 
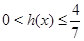и 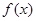монотонна на 
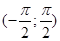, то уравнение 
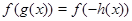равносильно уравнению 
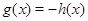, т.е. 
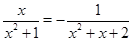, которое имеет единственный корень 
.
Ответ. 
.
Пример Решить уравнение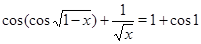 
.
Решение. На основании теоремы о производной сложной функции ясно, что функция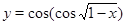 
убывающая (функция 
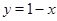убывающая, 
возрастающая,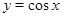 
убывающая). Отсюда понятно, что функция 
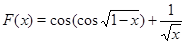определенная на 
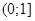, убывающая. Поэтому данное уравнение имеет не более одного корня. Так как 
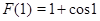, то
|
|
|
Ответ.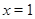 
.
Пример Решить уравнение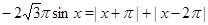 
.
Решение. Рассмотрим уравнение на трех промежутках.
а) Пусть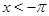 
. Тогда на этом множестве исходное уравнение равносильно уравнению 
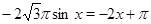. Которое на промежутке 
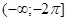решений не имеет, т. к. 
, 
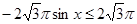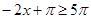, а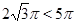 
. На промежутке 
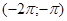исходное уравнение так же не имеет корней, т. к. 
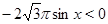, а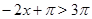 
.
б) Пусть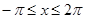 
. Тогда на этом множестве исходное уравнение равносильно уравнению
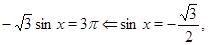
корнями которого на промежутке 
являются числа 
, 
, 
, 
.
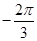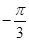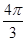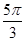в) Пусть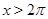 
. Тогда на этом множестве исходное уравнение равносильно уравнению
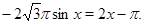
Которое на промежутке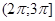 
решений не имеет, т. к. 
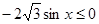, а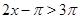 
. На промежутке 
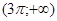уравнение так же решений не имеет, т. к. 
, 
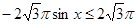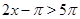, а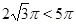 
.
Ответ.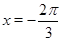 
, 
, 
, 
.
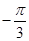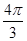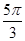Метод симметрии
Метод симметрии удобно применять, когда в формулировке задания присуствует требование единственности решения уравнения, неравенства, системы и т.п. или точное указание числа решений. При этом следует обнаружить какую-либо симметрию заданных выражений.
Нужно также учитывать многообразие различных возможных видов симметрии.
Не менее важным является четкое соблюдение логических этапов в рассуждениях с симметрией.
Обычно симметрия позволяет установить лишь необходимые условия, а затем требуется проверка их достаточности.
Пример Найти все значения параметра 
, при которых уравнение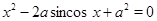 
имеет единственное решение.
Решение. Заметим, что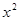 
и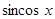 
--- четные функции, поэтому левая часть уравнения есть четная функция.
Значит если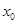 
--- решение уравнения, то 
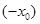есть также решение уравнения. Если 
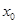--- единственное решение уравнения, то, необходимо, 
.
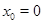Отберем возможные значения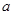 
, потребовав, чтобы 
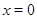было корнем уравнения.
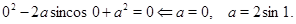
Сразу же отметим, что другие значения не могут удовлетворять условию задачи.
Но пока не известно, все ли отобранные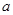 
в действительности удовлетворяют условию задачи.
|
|
|
Достаточность.
1) 
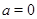, уравнение примет вид 
.
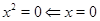2) 
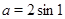, уравнение примет вид:
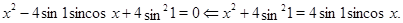
Очевидно, что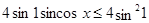 
, для всех 
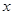и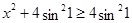 
. Следовательно, последнее уравнение равносильно системе:
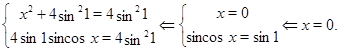
Тем самым, мы доказали, что при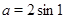 
, уравнение имеет единственное решение.
Ответ.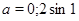 
.
|
|
|
