 |
Решение тригонометрических неравенств графическим методом
|
|
|
|
Заметим, что если 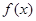 --- периодическая функция, то для решения неравенства
--- периодическая функция, то для решения неравенства 
 необходимо найти его решения на отрезке, длина которого равна периоду функции
необходимо найти его решения на отрезке, длина которого равна периоду функции 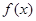 . Все решения исходного неравенства будут состоять из найденных значений
. Все решения исходного неравенства будут состоять из найденных значений  , а также всех
, а также всех  , отличающихся от найденных на любое целое число периодов функции
, отличающихся от найденных на любое целое число периодов функции  .
.
Рассмотрим решение неравенства  (
( ).
).
Поскольку 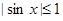 , то при
, то при 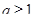 неравенство решений не имеет. Если
неравенство решений не имеет. Если 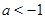 , то множество решений неравенства
, то множество решений неравенства 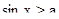 --- множество всех действительных чисел.
--- множество всех действительных чисел.
Пусть  . Функция синус имеет наименьший положительный период
. Функция синус имеет наименьший положительный период  , поэтому неравенство
, поэтому неравенство  можно решить сначала на отрезке длиной
можно решить сначала на отрезке длиной  , например, на отрезке
, например, на отрезке  . Строим графики функций
. Строим графики функций  и
и  (
( ).
).

На отрезке  функция синус возрастает, и уравнение
функция синус возрастает, и уравнение  , где
, где  , имеет один корень
, имеет один корень  . На отрезке
. На отрезке  функция синус убывает, и уравнение
функция синус убывает, и уравнение  имеет корень
имеет корень  . На числовом промежутке
. На числовом промежутке  график функции
график функции  расположен выше графика функции
расположен выше графика функции  . Поэтому для всех
. Поэтому для всех  из промежутка
из промежутка  ) неравенство
) неравенство  выполняется, если
выполняется, если  . В силу периодичности функции синус все решения неравенства
. В силу периодичности функции синус все решения неравенства  задаются неравенствами вида:
задаются неравенствами вида:  .
.
Аналогично решаются неравенства  ,
,  , и т.п.
, и т.п.
Пример Решим неравенство  .
.
Решение. Рассмотрим график функции 
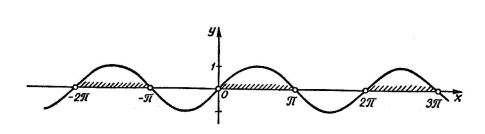
и выберем из промежутка 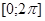 на оси
на оси  значения аргумента
значения аргумента  , которым соответствуют точки графика, лежащие выше оси
, которым соответствуют точки графика, лежащие выше оси  . Таким промежутком является интервал
. Таким промежутком является интервал  . Учитывая периодичность функции
. Учитывая периодичность функции  все решения неравенства
все решения неравенства  можно записать так:
можно записать так:  .
.
Ответ.  .
.
Пример Решите неравенство 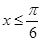 .
.
Решение. Нарисуем график функции  . Найдём точку пересечения этого графика с горизонтальной прямой
. Найдём точку пересечения этого графика с горизонтальной прямой  .
.

Это точка с абсциссой  . По графику видно, что для всех
. По графику видно, что для всех 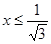 график функции лежит ниже прямой
график функции лежит ниже прямой  . Следовательно, эти
. Следовательно, эти  и составляют:
и составляют:
|
|
|
Ответ.  .
.
ОТБОР КОРНЕЙ
Проблема отбора корней, отсеивания лишних корней при решении тригонометрических уравнений весьма специфична и обычно оказывается более сложной, чем это имело место для уравнений алгебраических. Приведем решения уравнений, иллюстрирующие типичные случаи появления посторонних корней и методы <<борьбы>> с ними.
Пример Найти ближайший к числу  корень уравнения
корень уравнения

Решение.


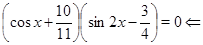

Подставляя последовательно в формулу  вместо переменной
вместо переменной  выписанные выше серии решений уравнений, отыщем для каждой из них
выписанные выше серии решений уравнений, отыщем для каждой из них  , а затем сравним полученные минимальные
, а затем сравним полученные минимальные 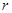 между собой.
между собой.
a) 
Ясно, что  достигается при
достигается при  , то есть
, то есть  .
.
б) 
 .
.
в)  .
.
г)  .
.
 .
.
Выберем минимальное из чисел 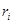 ,
,  . Сразу ясно, что
. Сразу ясно, что  и что
и что  . Оталось сравнить
. Оталось сравнить  и
и  . Предположим, что
. Предположим, что




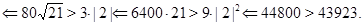
Последнее неравенство --- верное, а все сделанные переходы --- равносильные. Поэтому верно исходное неравенство. Обоснуем равносильность переходов (*) и (**) (равносильность остальных переходов следует из общих свойств числовых неравнств). В случае преобраования (*), достаточно заметить, что числа  и
и  расположен на участке
расположен на участке  монотонного возрастания функции
монотонного возрастания функции  . В случае перехода (**) формула
. В случае перехода (**) формула  справедлива, так как
справедлива, так как  .
.
Ответ.  .
.
Пример Найти корни уравнения: 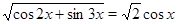 .
.
Решение этого уравнения распадается на два этапа: 1) решение уравнения, получающегося из данного возведением в квадрат обеих его частей; 2) отбор тех корней, которые удовлетворяют условию  . При этом заботится об условии
. При этом заботится об условии  нет необходимости. Все значения
нет необходимости. Все значения  , удовлетворяющие возведенному в квадрат уравнению, этому условию удовлетворяют.
, удовлетворяющие возведенному в квадрат уравнению, этому условию удовлетворяют.
Первый шаг нас приводит к уравнению 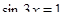 , откуда
, откуда  .
.
Теперь надо определить, при каких  будет
будет  . Для этого достаточно для
. Для этого достаточно для 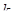 рассмотреть значения
рассмотреть значения 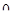 ,
,  ,
,  , т. е. <<обойти один раз круг>>, поскольку дальше значения косинуса начнут повторяться, получившиеся углы будут отличаться от уже рассмотренных на величину, кратную
, т. е. <<обойти один раз круг>>, поскольку дальше значения косинуса начнут повторяться, получившиеся углы будут отличаться от уже рассмотренных на величину, кратную  .
.
|
|
|
Ответ. 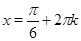 ,
,  .
.
Итак, основная схема отбора корней состоит в следующем. Находится наименьший общий период всех тригонометрических функций входящих в уравнение. На этом периоде отбираются корни, а затем оставшиеся корни периодически продолжаются.
Пример Решить уравнение:

Решение. Уравнение равносильно смешанной системе:
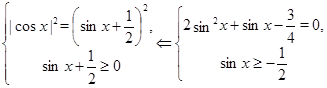

Но  --- не годится.
--- не годится.
Ответ.  .
.
Раскрывая знак модуля получаем более громоздное решение. А ответ в этом случае принимает вид:
Ответ.  .
.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Тест по теме <<Тригонометрические уравнения>>
• Объединение каких множеств  ,
,  ,
,  ,
,  является решением уравнения
является решением уравнения 
 ,
,  ,
,  ,
,  .
.
a)  ,
,  б)
б)  ,
,  в)
в)  ,
,  г)
г)  ,
, 
• Решите уравнение 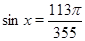 .
.
a)  б)
б)  в)
в)  г)
г) 
• Решите уравнение  .
.
a) 
б) 
в) 
г) 
• Решите уравнение  .
.
a) 
б) 
в) 
г) 
• Решите уравнение  .
.
a) 
б) 
в) 
г) 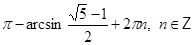
• Среди множеств  ,
,  найдите решение уравнения
найдите решение уравнения

и укажите те, которые не являются подмножествами друг друга.
 ,
,  ,
,  ,
,  ,
,  .
.
а)  б)
б)  в)
в)  г)
г) 
• Среди множеств  ,
,  найдите решение уравнения
найдите решение уравнения





а)  б)
б)  в)
в) 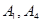 г)
г) 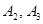
• Решите уравнение  .
.
а)  б)
б) 
в)  г)
г) 
• Решите уравнение

а) 
б) 
в) 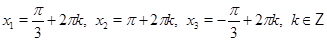
г) 
• Решите уравнение  .
.
а)  б)
б) 
в)  г)
г) 
• Сумма корней уравнения  на отрезке
на отрезке  равна:
равна:
а)  б)
б)  в)
в)  г)
г) 
• Решите уравнение

В ответе записать количество корней уравнения, принадлежащих отрезку  .
.
а)  б)
б)  в)
в)  г)
г) 
• Решить уравнение 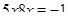
а)  б)
б) 
в)  г)
г) 
• Решите уравнение  .
.
a)  б)
б) 
в)  г)
г) 
• Решите уравнение
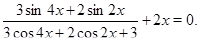
a) 
б) 
в) 
г) 
Найдите набольший отрицательный корень уравнения:

a)  б)
б) 
в)  г)
г) 
• Решите уравнение 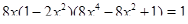 на множестве
на множестве  .
.
a) 
б) 
в) 
г) 
• Решите уравнение 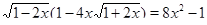 .
.
a)  б)
б) 
в)  г)
г) 
• Решить уравнение 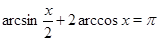 .
.
а)  б)
б)  в)
в)  г)
г) 
• Решите уравнение  .
.
a) 
б)  или
или 
в)  или
или  и
и 
г)  или
или  и
и 
Ответы 1а 2б 3б 4г 5б 6б 7а 8б 9г 10б 11а 12б 13в или г 14а 15в 16в 17в 18а или б 19г 20в
ЗАКЛЮЧЕНИЕ
В данной работе были рассмотрены методы решения тригонометрических уравнений и неравенств, как простейших, так и олимпиадного уровня. Были рассмотрены основные методы решения тригонометрических уравнений и неравенств, причем, как специфические --- характерные только для тригонометрических уравнений и неравенств,--- так и общие функциональные методы решения уравнений и неравенств, применительно к тригонометрическим уравнениям.
|
|
|
В дипломной работе приведены основные теоретические сведения: определение и свойства тригонометрических и обратных тригонометрических функций; выражение тригонометрических функций через другие тригонометрических функции, что очень важно для преобразования тригонометрических выражений, в особенности содержащих обратные тригонометрические функции; кроме основных тригонометрических формул, хорошо известных из школьного курса, приведены формулы упрощающие выражения, содержащие обратные тригонометрические функции. Рассмотрены решение элементарных тригонометрических уравнений, метод разложения на множители, методы сведения тригонометрических уравнений к алгебраическим. Ввиду того, что решения тригонометрических уравнений можно записать несколькими способами, и вид этих решений не позволяет сразу установить, являются ли эти решения одинаковыми или различными, рассмотрена общая схема решения тригонометрических уравнений и подробно рассмотрено преобразование групп общих решений тригонометрических уравнений. Подробно рассмотрены методы решения элементарных тригонометрических неравенств, как на единичной окружности, так и графическим методом. Описан процесс решения неэлементарных тригонометрических неравенств через элементарные неравенства и уже хорошо известный школьникам метод интервалов. Приведены решения типичных заданий на отбор корней. Приведены необходимые теоретических сведения для отбора корней: разбиение множества целых чисел на непересекающиеся подмножества, решение уравнений в целых числах (диафантовых).
Результаты данной дипломной работы могут быть использованы в качестве учебного материала при подготовке курсовых и дипломных работ, при составлении факультативов для школьников, так же работа может применяться при подготовке учащихся к вступительным экзаменам и централизованному тестированию.
|
|
|
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
Выгодский Я.Я., Справочник по элементарной математике. /Выгодский Я.Я. --- М.: Наука, 1970.
Игудисман О., Математика на устном экзамене/ Игудисман О. --- М.: Айрис пресс, Рольф, 2001.
Азаров А.И., уравнения/Азаров А.И., Гладун О.М., Федосенко В.С. --- Мн.: Тривиум, 1994.
Литвиненко В.Н., Практикум по элементарной математике / Литвиненко В.Н.--- М.: Просвещение, 1991.
Шарыгин И.Ф., Факультативный курс по математике: решение задач/ Шарыгин И.Ф., Голубев В.И. --- М.: Просвещение, 1991.
Бардушкин В., Тригонометрические уравнения. Отбор корней/В. Бардушкин, А. Прокофьев.// Математика, №12, 2005 с. 23--27.
Василевский А.Б., Задания для внеклассной работы по математике/Василевский А.Б. --- Мн.: Народная асвета. 1988. --- 176с.
Сапунов П. И., Преобразование и объединение групп общих решений тригонометрических уравнений/Сапунов П. И. // Математическое просвещение, выпуск №3, 1935.
Бородин П., Тригонометрия. Материалы вступительных экзаменов в МГУ[текст]/П.Бородин, В.Галкин, В.Панфёров, И.Сергеев, В.Тарасов // Математика №1, 2005 с. 36--48.
Самусенко А.В., Математика: Типичные ошибки абитуриентов: Справочное пособие/Самусенко А.В., Казаченок В.В.--- Мн.: Вышейшая школа, 1991.
Азаров А.И., Функциональный и графический методы решения экзаменационных задач/Азаров А.И., Барвенов С.А.,--- Мн.: Аверсэв, 2004.
|
|
|


