 |
Универсальная тригонометрическая подстановка
|
|
|
|
Тригонометрическое уравнение вида
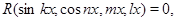
где 
--- рациональная функция с помощью фомул --, а так же с помощью формул -- можно свести к рациональному уравнению относительно аргументов 
, 
, 
, , после чего уравнение может быть сведено к алгебраическому рациональному уравнению относительно 
с помощью формул универсальной тригонометрической подстановки
Следует отметить, что применение формул может приводить к сужению ОДЗ исходного уравнения, поскольку 
не определен в точках 
, поэтому в таких случаях нужно проверять, являются ли углы 
, корнями исходного уравнения.
Пример Решить уравнение 
.
Решение. По условию задачи 
. Применив формулы и сделав замену 
, получим
откуда 
и, следовательно, 
.
Уравнения вида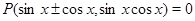 
Уравнения вида 
, где 
--- многочлен, решаются с помощью замен неизвестных
Пример Решить уравнение 
.
Решение. Сделав замену и учитывая, что 
, получим
откуда 
, 
. 
--- посторонний корень, т.к. 
. Корнями уравнения 
являются 
.
НЕСТАНДАРТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ
Использование ограниченности функций
В практике централизованного тестирования не так уж редко встречаются уравнения, решение которых основывается на ограниченности функций 
и 
. Например:
Пример Решить уравнение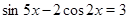 
.
Решение. Поскольку 
, 
, то левая часть не превосходит 
и равна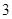 
, если 
Для нахождения значений , удовлетворяющих обоим уравнениям, поступим следующим образом. Решим одно из них, затем среди найденных значений отберем те, которые удовлетворяют и другому.
Начнем со второго: 
, 
. Тогда 
, 
.
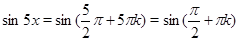Понятно, что лишь для четных 
будет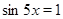 
.
Ответ.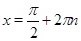 
.
|
|
|
Другая идея реализуется при решении следующего уравнения:
Пример Решить уравнение 
.
Решение. Воспользуемся свойством показательной функции: 
, 
.
Сложив почленно эти неравенства будем иметь:
Следовательно левая часть данного уравнения равна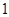 
тогда и только тогда, когда выполняются два равенства:
т. е.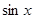 
может принимать значения 
, 
, 
, а 
может принимать значения 
, .
Ответ. , 
.
Пример Решить уравнение 
.
Решение.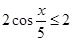 
, 
. Следовательно, 
.
Ответ. 
.
Пример Решить уравнение
Решение. Обозначим 
, тогда из определения обратной тригонометрической функции 
имеем 
и 
.
Так как 
, то из уравнения следует неравенство 
, т.е. 
. Поскольку 
и , то 
и 
. Однако 
и поэтому 
.
Если и 
, то 
. Так как ранее было установлено, что 
, то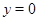 
.
Ответ.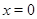 
, 
.
Пример Решить уравнение
Решение. Областью допустимых значений уравнения являются 
.
Первоначально покажем, что функция
при любых 
может принимать только положительные значения.
Представим функцию 
следующим образом: 
.
Поскольку 
, то имеет место 
, т.е. 
.
Следовательно, для доказательства неравенства 
, необходимо показать, что 
. С этой целью возведем в куб обе части данного неравенства, тогда
Полученное численное неравенство свидетельствует о том, что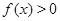 
. Если при этом еще учесть, что 
, то левая часть уравнения неотрицательна.
Рассмотрим теперь правую часть уравнения.
Так как 
, то
.
Однако известно, что 
. Отсюда следует, что 
, т.е. правая часть уравнения не превосходит 
. Ранее было доказано, что левая часть уравнения неотрицательна, поэтому равенство в может быть только в том случае, когда обе его части равны 
, а это возможно лишь при 
.
Ответ. .
Пример Решить уравнение
Решение. Обозначим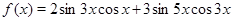 
и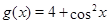 
. Применяя неравенство Коши-Буняковского, получаем 
. Отсюда следует, что 
. C другой стороны имеет место 
. Следовательно, уравнение не имеет корней.
|
|
|
Ответ. 
.
Пример Решить уравнение:
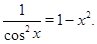
Решение. Перепишем уравнение в виде:
Ответ. .
|
|
|
