 |
Решение с исследованием функции
|
|
|
|
Пример Докажите, что все решения уравнения

--- целые числа.
Решение. Основной период исходного уравнения равен  . Поэтому сначала исследуем это уравнение на отрезке
. Поэтому сначала исследуем это уравнение на отрезке  .
.
Преобразуем уравнение к виду:

При помощи микрокалькулятора получаем:

Находим:

Если  , то из предыдущих равенств получаем:
, то из предыдущих равенств получаем:

Решив полученное уравнение, получим:  .
.
Выполненные вычисления представляют возможность предположить, что корнями уравнения, принадлежащими отрезку 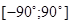 , являются
, являются 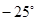 ,
,  и
и  .
.
Непосредственная проверка подтверждает эту гипотезу. Таким образом, доказано, что корнями уравнения являются только целые числа  ,
, 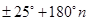 .
.
Пример Решите уравнение  .
.
Решение. Найдём основной период уравнения. У функции 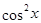 основной период равен
основной период равен  . Основной период функции
. Основной период функции 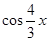 равен
равен 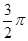 . Наименьшее общее кратное чисел
. Наименьшее общее кратное чисел  и
и 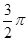 равно
равно  . Поэтому основной период уравнения равен
. Поэтому основной период уравнения равен 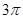 . Пусть
. Пусть  .
.
Очевидно,  является решением уравнения. На интервале
является решением уравнения. На интервале  . Функция
. Функция  отрицательна. Поэтому другие корни уравнения следует искать только на интервалаx
отрицательна. Поэтому другие корни уравнения следует искать только на интервалаx  и
и 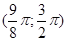 .
.
При помоши микрокалькулятора сначала найдем приближенные значения корней уравнения. Для этого составляем таблицу значений функции 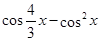 на интервалах
на интервалах  и
и  ; т. е. на интервалах
; т. е. на интервалах  и
и  .
.

| 
| 
| 
|
| 0 | 0 | 202,5 | 0,85355342 |
| 3 | -0,00080306 | 207 | 0,6893642 |
| 6 | -0,00119426 | 210 | 0,57635189 |
| 9 | -0,00261932 | 213 | 0,4614465 |
| 12 | -0,00448897 | 216 | 0,34549155 |
| 15 | -0,00667995 | 219 | 0,22934931 |
| 18 | -0,00903692 | 222 | 0,1138931 |
| 21 | -0,01137519 | 225 | 0,00000002 |
| 24 | -0,01312438 | 228 | -0,11145712 |
| 27 | -0,01512438 | 231 | -0,21961736 |
| 30 | -0,01604446 | 234 | -0,32363903 |
| 33 | -0,01597149 | 237 | -0,42270819 |
| 36 | -0,01462203 | 240 | -0,5160445 |
| 39 | -0,01170562 | 243 | -0,60290965 |
| 42 | -0,00692866 | 246 | -0,65261345 |
| 45 | 0,00000002 | 249 | -0,75452006 |
| 48 | 0,00936458 | 252 | -0,81805397 |
| 51 | 0,02143757 | 255 | -0,87270535 |
| 54 | 0,03647455 | 258 | -0,91803444 |
| 57 | 0,0547098 | 261 | -0,95367586 |
| 60 | 0,07635185 | 264 | -0,97934187 |
| 63 | 0,10157893 | 267 | -0,99482505 |
| 66 | 0,1305352 | 270 | -1 |
| 67,5 | 0,14644661 |
Из таблицы легко усматриваются следующие гипотезы: корнями уравнения, принадлежащими отрезку 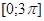 , являются числа:
, являются числа:  ;
; 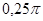 ;
;  . Непосредственная проверка подтверждает эту гипотезу.
. Непосредственная проверка подтверждает эту гипотезу.
|
|
|
Ответ.  ;
;  ;
;  .
.
ТРИГОНОМЕТРИЧЕСКИЕ НЕРАВЕНСТВА
Решение тригонометрических неравенств с помощью единичной окружности
При решении тригонометрических неравенств вида 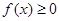 , где
, где 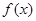 --- одна из тригонометрических функций, удобно использовать тригонометрическую окружность для того, чтобы наиболее наглядно представить решения неравенства и записать ответ. Основным методом решения тригонометрических неравенств является сведение их к простейшим неравенствам типа
--- одна из тригонометрических функций, удобно использовать тригонометрическую окружность для того, чтобы наиболее наглядно представить решения неравенства и записать ответ. Основным методом решения тригонометрических неравенств является сведение их к простейшим неравенствам типа  . Разберём на примере, как решать такие неравенства.
. Разберём на примере, как решать такие неравенства.
Пример Решите неравенство  .
.
Решение. Нарисуем тригонометрическую окружность и отметим на ней точки, для которых ордината превосходит  .
.

Для  решением данного неравенства будут
решением данного неравенства будут  . Ясно также, что если некоторое число
. Ясно также, что если некоторое число  будет отличаться от какого-нибудь числа из указанного интервала на
будет отличаться от какого-нибудь числа из указанного интервала на 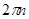 , то
, то 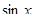 также будет не меньше
также будет не меньше  . Следовательно, к концам найденного отрезка решения нужно просто добавить
. Следовательно, к концам найденного отрезка решения нужно просто добавить 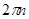 . Окончательно, получаем, что решениями исходного неравенства будут все
. Окончательно, получаем, что решениями исходного неравенства будут все  .
.
Ответ. 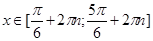 .
.
Для решения неравенств с тангенсом и котангенсом полезно понятие о линии тангенсов и котангенсов. Таковыми являются прямые  и
и  соответственно (на рисунке (1) и (2)), касающиеся тригонометрической окружности.
соответственно (на рисунке (1) и (2)), касающиеся тригонометрической окружности.

Легко заметить, что если построить луч с началом в начале координат, составляющий угол  с положительным направлением оси абсцисс, то длина отрезка от точки
с положительным направлением оси абсцисс, то длина отрезка от точки 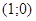 до точки пересечения этого луча с линией тангенсов в точности равна тангенсу угла, который составляет этот луч с осью абсцисс. Аналогичное наблюдение имеет место и для котангенса.
до точки пересечения этого луча с линией тангенсов в точности равна тангенсу угла, который составляет этот луч с осью абсцисс. Аналогичное наблюдение имеет место и для котангенса.
|
|
|
Пример Решите неравенство  .
.
Решение. Обозначим  , тогда неравенство примет вид простейшего:
, тогда неравенство примет вид простейшего:  . Рассмотрим интервал
. Рассмотрим интервал  длиной, равной наименьшему положительному периоду (НПП) тангенса. На этом отрезке с помощью линии тангенсов устанавливаем, что
длиной, равной наименьшему положительному периоду (НПП) тангенса. На этом отрезке с помощью линии тангенсов устанавливаем, что  . Вспоминаем теперь, что необходимо добавить
. Вспоминаем теперь, что необходимо добавить  , поскольку НПП функции
, поскольку НПП функции 
 . Итак,
. Итак,  . Возвращаясь к переменной
. Возвращаясь к переменной  , получаем, что
, получаем, что 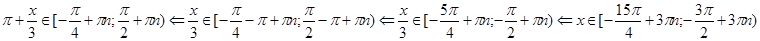 .
.
Ответ. 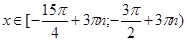 .
.
Неравенства с обратными тригонометрическими функциями удобно решать с использованием графиков обратных тригонометрических функций. Покажем, как это делается на примере.
|
|
|


