 |
Синус, косинус, тангенс и котангенс накрепко связаны со своими углами. Знаем одно - значит, знаем и другое.
|
|
|
|
Другими словами, у каждого угла есть свой неизменный синус и косинус. И почти у каждого - свой тангенс и котангенс. Почему почти? Об этом ниже.
Это знание здорово помогает в учёбе! Существует масса заданий, где требуется перейти от синусов к углам и наоборот. Для этого существует таблица синусов. Аналогично, для заданий с косинусом - таблица косинусов. И, как вы уже догадались, существует таблица тангенсов и таблица котангенсов.)
Таблицы бывают разные. Длинные, где можно посмотреть, чему равен, скажем, sin37°6’. Раскрываем таблицы Брадиса, ищем угол тридцать семь градусов шесть минут и видим значение 0,6032. Понятное дело, запоминать это число (и тысячи других табличных значений) совершенно не требуется.
В сущности, в наше время длинные таблицы косинусов синусов тангенсов котангенсов не особо-то и нужны. Один хороший калькулятор заменяет их полностью. Но знать о существовании таких таблиц не мешает. Для общей эрудиции.)
И зачем тогда этот урок?! - спросите вы.
А вот зачем. Среди бесконечного количества углов существуют особые, о которых вы должны знать всё. На этих углах построена вся школьная геометрия и тригонометрия. Это, своего рода, "таблица умножения" тригонометрии. Если вы не знаете, чему равен, например, sin50°, никто вас не осудит.) Но если вы не знаете, чему равен sin30°, будьте готовы получить заслуженную двойку...
Таких особых углов тоже прилично набирается. Школьные учебники обычно любезно предлагают к запоминанию таблицу синусов и таблицу косинусов для семнадцати углов. Ну и, разумеется, таблицу тангенсов и таблицу котангенсов для тех же семнадцати углов... Т.е. предлагается запомнить 68 значений. Которые, между прочим, очень похожи между собой, то и дело повторяются и меняют знаки. Для человека без идеальной зрительной памяти - та ещё задачка...)
|
|
|
Мы пойдём другим путём. Заменим механическое запоминание на логику и смекалку. Тогда нам придётся зазубрить 3 (три!) значения для таблицы синусов и таблицы косинусов. И 3 (три!) значения для таблицы тангенсов и таблицы котангенсов. И всё. Шесть значений запомнить легче, чем 68, мне кажется...)
Все остальные необходимые значения мы будем получать из этих шести с помощью мощной законной шпаргалки- тригонометрического круга. Если вы не изучали эту тему, сходите по ссылочке, не ленитесь. Этот круг не только для этого урока нужен. Он незаменим для всей тригонометрии сразу. Не пользоваться таким инструментом просто грех! Не хотите? Дело ваше. Заучивайте таблицу синусов. Таблицу косинусов. Таблицу тангенсов. Таблицу котангенсов. Все 68 значений для разнообразных углов.)
Итак, начнём. Для начала разобьём все эти особые углы на три группы.
Первая группа углов.
Рассмотрим первую группауглов из семнадцати особых. Это 5 углов: 0°, 90°, 180°, 270°, 360°.
Вот так выглядит таблица синусов косинусов тангенсов котангенсов для этих углов:
| Угол х (в градусах) | |||||
| Угол х (в радианах) | 
| 
| 
| 
| |
| sin x | -1 | ||||
| cos x | -1 | ||||
| tg x | не сущ. | не сущ. | |||
| ctg x | не сущ. | не сущ. | не сущ. |
Желающие запомнить - запоминайте. Но сразу скажу, что все эти единички и нолики очень путаются в голове. Гораздо сильнее, чем хочется.) Поэтому включаем логику и тригонометрический круг.
Рисуем круг и отмечаем на нём эти самые углы: 0°, 90°, 180°, 270°, 360°. Я эти углы отметил красными точками:
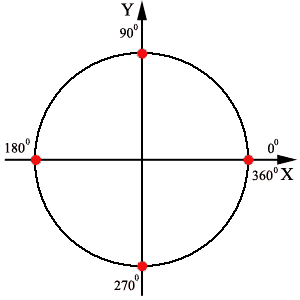
Сразу видно, в чём особенность этих углов. Да! Это углы, которые попадают точно на оси координат! Собственно, поэтому-то и путается народ... Но мы путаться не будем. Разберёмся, как находить тригонометрические функции этих углов без особого запоминания.
|
|
|
Кстати, положение угла в 0 градусов полностью совпадает с положением угла в 360 градусов. Это значит, что синусы, косинусы, тангенсы у этих углов совершенно одинаковы. Угол в 360 градусов я отметил, чтобы замкнуть круг.
Предположим, в сложной стрессовой обстановке ЕГЭ вы как-то засомневались... Чему равен синус 0 градусов? Вроде ноль... А вдруг единица?! Механическое запоминание такая штука. В суровых условиях сомнения грызть начинают...)
Спокойствие, только спокойствие!) Я подскажу вам практический приём, который выдаст стопроцентно правильный ответ и начисто уберёт все сомнения.
В качестве примера разберёмся, как чётко и надёжно определить, скажем, синус 0 градусов. А заодно, и косинус 0. Именно в этих значениях, как ни странно, частенько люди путаются.
Для этого на круге нарисуем произвольный угол х. В первой четверти, чтобы недалеко от 0 градусов было. Отметим на осях синус и косинус этого угла х, всё чин-чинарём. Вот так:
А теперь - внимание! Уменьшим угол х, приблизим подвижную сторону к оси ОХ. Наведите курсор на картинку и всё увидите.
Теперь включаем элементарную логику!. Смотрим и размышляем: как ведёт себя sinx при уменьшении угла х? При приближении угла к нулю? Он уменьшается! А cosx - увеличивается! Остаётся сообразить, что станет с синусом, когда угол схлопнется совсем? Когда подвижная сторона угла (точка А) уляжется на ось ОХ и угол станет равным нулю? Очевидно, и синус угла уйдёт в ноль. А косинус увеличится до... до... Чему равна длина подвижной стороны угла (радиус тригонометрического круга)? Единице!
Вот и ответ. Синус 0 градусов равен 0. Косинус 0 градусов равен 1. Совершенно железно и безо всяких сомнений!) Просто потому, что иначе быть не может.
Совершенно аналогично можно узнать (или уточнить) синус 270 градусов, например. Или косинус 180. Нарисовать круг, произвольный угол в четверти рядышком с интересующей нас осью координат, мысленно подвигать сторону угла и уловить, чем станет синус и косинус, когда сторона угла уляжется на ось. Вот и всё.
Как видите, для этой группы углов ничего заучивать не надо. Не нужна здесь таблица синусов... Да и таблица косинусов - тоже.) Кстати, после нескольких применений тригонометрического круга все эти значения запомнятся сами по себе. А если забудутся - нарисовал за 5 секунд круг и уточнил. Куда проще, чем звонить другу из туалета с риском для аттестата, правда?)
|
|
|
Что касается тангенса и котангенса - всё то же самое. Рисуем на круге линию тангенса (котангенса) - и всё сразу видно. Где они равны нулю, а где - не существуют. Что, не знаете про линии тангенса и котангенса? Это печально, но поправимо.) Посетили Раздел 555 Тангенс и котангенс на тригонометрическом круге - и нет проблем!
Если вы поняли, как чётко определить синус, косинус, тангенс и котангенс для этих пяти углов - я вас поздравляю! На всякий случай сообщаю, что вы теперь можете определять функции любых углов, попадающих на оси. А это и 450°, и 540°, и 1800°, и ещё бесконечное количество...) Отсчитал (правильно!) угол на круге - и нет проблем с функциями.
Но, как раз, с отсчётом углов и случаются проблемы да ошибки... Как их избежать, написано в уроке: Как нарисовать (отсчитать) любой угол на тригонометрическом круге в градусах. Элементарно, но очень помогает в борьбе с ошибками.)
А вот урок: Как нарисовать (отсчитать) любой угол на тригонометрическом круге в радианах - покруче будет. В смысле возможностей. Скажем, определить на какую из четырёх полуосей попадает угол

вы сможете за пару секунд. Я не шучу! Именно за пару секунд. Ну конечно, не только 345 "пи"...) И 121, и 16, и -1345. Любой целый коэффициент годится для мгновенного ответа.
А если угол

Подумаешь! Верный ответ получается секунд за 10. Для любого дробного значения радианов с двойкой в знаменателе.
Собственно, этим и хорош тригонометрический круг. Тем, что умение работать с некоторыми углами он автоматически расширяет на бесконечное множество углов.
Итак, с пятью углами из семнадцати - разобрались.
Вторая группа углов.
Следующая группа углов - это углы 30°, 45° и 60°. Почему именно эти, а не, к примеру, 20, 50 и 80? Да как-то сложилось так... Исторически.) Дальше будет видно, чем хороши эти углы.
|
|
|
Таблица синусов косинусов тангенсов котангенсов для этих углов выглядит так:
| Угол х (в градусах) | |||||
| Угол х (в радианах) | 
| 
| 
| 
| |
| sin x | 
| 
| 
| ||
| cos x | 
| 
| 
| ||
| tg x | 
| 
| не сущ. | ||
| ctg x | не сущ. | 
| 
|
Я оставил значения для 0° и 90° из предыдущей таблицы для завершённости картины.) Чтобы было видно, что эти углы лежат в первой четверти и возрастают. От 0 до 90. Это пригодится нам дальше.
Значения таблицы для углов 30°, 45° и 60° надо запомнить. Зазубрить, если хотите. Но и здесь есть возможность облегчить себе жизнь.) Обратите внимание на значения таблицы синусов этих углов. И сравните со значениями таблицы косинусов...
Да! Они одни и те же! Только расположены в обратном порядке. Углы возрастают (0, 30, 45, 60, 90) - и значения синуса возрастают от 0 до 1. Можете убедиться с калькулятором. А значения косинуса - убывают от 1 до нуля. Причём, сами значения одни и те же. Для углов 20, 50, 80 так бы не получилось...
Отсюда полезный вывод. Достаточно выучить три значения для углов 30, 45, 60 градусов. И помнить, что у синуса они возрастают, а у косинуса - убывают. Навстречу синусу.) На половине пути (45°) они встречаются, т.е синус 45 градусов равен косинусу 45 градусов. А дальше опять расходятся... Три значения можно выучить, правда?
С тангенсами - котангенсами картина исключительно та же самая. Один в один. Только значения другие. Эти значения (ещё три!) тоже надо выучить.
Ну вот, практически всё запоминание и закончилось. Вы поняли (надеюсь), как определять значения для пяти углов попадающих на оси и выучили значения для углов 30, 45, 60 градусов. Всего 8.
Осталось разобраться с последней группой из 9 углов.
Вот эти углы:
120°; 135°; 150°; 210°; 225°; 240°; 300°; 315°; 330°. Для этих углов надо железно знать таблицу синусов, таблицу косинусов и т.д.
Кошмар, правда?)
А если добавить сюда углы, типа: 405°, 600°, или 3000° и много-много такого же красивого?)
Или углы в радианах? Например, про углы:

и многие другие, вы должны знать всё.
Самое забавное, что знать это всё - невозможно в принципе. Если использовать механическую память.
И очень легко, фактически элементарно - если использовать тригонометрический круг. Если вы освоите практическую работу с тригонометрическим кругом, все эти ужасные углы в градусах будут легко и элегантно сводиться к старым добрым:
30°, 45°, 60°
А лохматые углы в радианах превратятся в привычные:



Причём в радианах это превращение делается куда проще, чем в градусах. Да-да!
Плюс к тому, умение рисовать углы на круге позволяет элементарно разобраться с последней, третьей группой углов. И тогда, в 99% заданий, таблица синусов и таблица косинусов вам точно не потребуются. Как и таблица тангенсов-котангенсов).
|
|
|
Все тайны последней, третьей группы особенных углов и секреты уверенной работы с ними - в следующем уроке.
Таблица синусов и косинусов.
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно "не очень..."
И для тех, кто "очень даже...")
Продолжаем осваивать таблицу синусов и косинусов. А именно - привыкаем работать с необходимыми табличными значениями без механической зубрёжки. И, разумеется, без бумажек-шпаргалок. Это несложно. Если голову включить. Голова нужна не только шапку носить, да...)
Итак, в предыдущем уроке мы разбили углы, про которые нужно знать всё, на три группы. Первая группа - углы, попадающие точно на оси координат. Вторая группа - всего три угла: 30°, 45°, 60°. Значения таблицы синусов и косинусов для этих трёх углов приходится-таки вызубрить. Аж все три значения!)
Осталась последняя, третья группа углов.
Третья группа углов.
Вот эти девять углов:
120°; 135°; 150°; 210°; 225°; 240°; 300°; 315°; 330°.
Надо железно знать таблицу синусов и косинусов для этих углов. Вот как выглядят эти углы в радианах:

| 
| 
| 
| 
| 
| 
| 
| 
|
Для пущего устрашения я добавлю, что это углы, которые лежат в пределах всего лишь одного оборота. Т.е в пределах 360°. А надо знать значения таблицы синусов и косинусов и за этими пределами... Скажем, синус 855°, или косинус 21пи/4 вы знать обязаны.
Что, меркнут краски жизни!?)
Спокойствие! Нас спасут житейская смекалка и тригонометрический круг! Я же предупреждал, что с помощью круга все эти несусветные проблемы (и не только эти!) можно решить за пару минут. Слегка скучая.)
В конце предыдущего урока я задавал вопрос: чего особенного в этих девяти углах? Кто сообразил, тот справится. Кто не сообразил, тот прямо сейчас узнает тайну этих углов и тоже справится! Внимайте!
Дело в том, что все эти углы составлены из углов предыдущих двух групп. Например:
120° = 90° + 30°
225° = 180° + 45°
300° = 270° + 30°
Ну, вы поняли...)
Кстати, можно использовать не сумму, а разность, например:
300° = 360° - 60°
135° = 180° - 45°
И так далее.
Другими словами, каждый угол из этой группы есть сумма (разность) одного угла из первой группы (те, что попадают на оси координат) и одного угла из второй группы (30, 45, 60). Нет, можно конечно разбить углы на сумму/разность каких попало, но оно нам совсем не надо.) Надо: один угол - из первой группы и один из второй.
И как же мы будем использовать этот замечательный факт? Просто складывать-вычитать синусы? Разочарую... Синус суммы углов вовсе не равен сумме синусов каждого угла! Запомните это накрепко! Для суммы есть своя длинная формула. Но такое особое устройство углов позволит нам находить их синусы-косинусы одной левой.) Без таблицы синусов и косинусов.
Здесь нет никакой особой теории. Чистая практика! Поэтому показываю на примерах.
Итак, пусть нам надо найти косинус 150 градусов. Подозреваю, что далеко не каждый сразу и уверенно вспомнит это значение таблицы синусов и косинусов. Ох, не каждый...) А если и вспомнит, сомнения будут грызть. Посему работаем надёжно!
Прежде всего соображаем, из каких особых углов он состоит. Рекомендую в качестве угла из первой группы выбирать 180° или 360° Далее поймёте, почему. Легко сообразить, что:
150° = 180° - 30°
Отлично! Разложился угол классически. Один - из первой группы, другой - из второй. Теперь нарисуем угол 150° на тригонометрическом круге. На глаз нарисуем, примерно. Но рисовать будем, глядя на разложение:
150° = 180° - 30°
Говоря житейским языком, мы крутим подвижную сторону угла (где точка А) на 180° в плюс (по часовой стрелке), затем отматываем угол на 30° обратно!) Надеюсь, вы уже знаете, как отсчитывать углы на тригонометрическом круге? Без этих знаний - никак...
Получаем вот такую картинку:
Зелёным цветом обозначен нужный нам угол в 150° и его косинус. А вот красным цветом я обозначил вспомогательный угол в 30°, который нас и спасёт в этой крутой задаче.) Ведь мы знаем (ну, или должны знать...) косинус 30 градусов из таблицы синусов и косинусов. Правда эти красненькие 30° как бы не совсем правильные 30°, не от той полуоси отсчитаны....
Ну и ладно. Давайте нарисуем правильные 30° на этом же круге. Отсчитанные от положительной полуоси Х. Наводим мышку на рисунок (кликать не надо, а то придётся всё сначала читать)) и видим правильный синий угол в 30° и его косинус.
Ну и...? Как вам кажется, в каком соотношении находятся cos30° и cos150°? Догадаетесь!?
Да! Косинус 150 градусов равен по величине косинусу 30, но имеет отрицательный знак! Треугольнички слева-справа одинаковые, косинусы равны по величине. Вот и всё. Просто мы на тригонометрическом круге просчитали непонятный косинус 150 градусов через известный косинус 30. Не заглядывая в таблицу синусов и косинусов. Так можно делать всегда.
Ответ:
| cos150° | = | -cos30° | = | - | 
|
А если нужен синус 150 градусов? Нет проблем! Опять рисуем круг, угол в 150 градусов (как 180° - 30°). На этот раз отмечаем его синус на оси У. Вот так:
Опять рисуем правильный угол в 30 градусов и отмечаем его синус. Наведите курсор на картинку, чтобы увидеть это сложное построение.) Что мы видим? Мы видим, что синусы углов 150° и 30° равны! Треугольнички-то одинаковые. Пусть даже и углы по 30° находятся вне треугольников. Всё равно, треугольнички - одинаковые.
Ответ:
| sin150° | = | sin30° | = | 
|
Улавливаете суть? Любой угол третьей группы всегда разбивается на сумму/разность угла 180° (или 360°) и угла 30, 45, 60 (какой уж подойдёт). Стало быть, на тригонометрическом круге мы всегда получим вспомогательный угол 30, 45 или 60 градусов. Без разницы, в какой четверти получится этот вспомогательный угол. Достаточно нарисовать правильный угол (в первой четверти), найти одинаковые треугольнички и сравнить по картинке их синусы-косинусы. Тут ошибиться очень трудно!
И не надо зазубривать таблицу синусов и косинусов для этих девяти углов.
Вот и всё. Есть тут, правда одна проблемка. Ленятся люди рисовать круг. Стесняются, что плохо получится, что ли!? Тригонометрический круг - легальная шпаргалка - нужен вам, а не проверяющим! Здесь не требуются линейка, циркуль, транспортир и прочие цветные карандаши. Не черчение, чай...
Так и быть, я личным примером покажу, как выглядит все это рисование в реале!
Пусть мне надо определить cos240°. Без таблицы синусов и косинусов. За пять секунд я соображаю, что:
240° = 180° + 60°
Ещё за десять секунд я рисую мощную картину:

М-да... Ужас какой-то. Ну и что!? Зато я чётко вижу, где располагается мой вспомогательный угол в 60° (третья четверть). Я знаю, что треугольнички, образованные вспомогательным углом в 60° и правильным углом в 60° (в первой четверти) - одинаковые. Пусть даже на картинке они, гм... не очень равны.) И по этой картинке я стопроцентно понимаю, что косинус 240 градусов равен косинусу 60, но со знаком "минус". Так как cos240° попадает на отрицательную полуось Х. Посему из этой кошмарной картины я надёжно вывожу (за 20 секунд!) правильный ответ. Безо всякой таблицы синусов и косинусов:
cos240° = - cos60° = - 1/2
Что мне и надо.)
Тем, кто проникся уважением к тригонометрическому кругу, предлагаю загадку. Как вы думаете, какую функцию и какого положительного угла я искал вот по этому наскальному рисунку?)

Если поняли, вам можно начинать изучать иероглифы.) Ответ будет чуть ниже.
Итак, осталось всего ничего. Разобраться с углами, которые больше 360°. Если они приводятся к углам второй группы (30, 45, 60), значения таблицы синусов и косинусов для них тоже знать необходимо. Ну, не совсем знать - таких углов бесконечное множество - но уметь их вычислять.
Здесь всё просто. Опять сплошная практика. Берём пример из начала урока. Пусть нам надо определить sin855°. Понятно, что в этом угле сидит несколько полных оборотов по 360° и ещё какой-то хвостик. Вот и выбросим эти полные обороты. Они никак не сказываются на тригонометрических функциях угла! Только картину путают...
Еслиу нас на круге есть угол, скажем, в 45°, то прибавьте к нему хоть пять полных оборотов, хоть тридцать пять - положение его не изменится. Не поменяются значения синусов, косинусов и т.д.
Определить количество полных оборотов очень просто. Надо разделить величину угла (в нашем случае - 855°) на 360°. Хоть в уме, хоть уголком. Радует то, что до конца делить не надо! Нам же количество целых оборотов надо знать, а не дробных.
Вот и делим. Получаем два с копейками. Копейки нас не интересуют, их даже и считать не нужно. А два полных оборота - это 2 · 360° = 720°. Считаем хвостик. Отнимаем:
855 - 720 = 135
Хвостик получился 135°. А это классический угол третьей группы! Так как:
135° = 180° - 45°
С этим углом разбираемся, как написано выше. С помощью круга. Вот и все дела. Так нужно поступать всегда. Откинуть от большого значения угла все полные обороты и работать с оставшимся хвостиком. Кстати, если этот хвостик не попадает ни в какую группу (20°, например, или 160°) - значит, где-то ошибка. Или задание - более сложное и рассчитано на какие-то дополнительные преобразования. Синус 20° вы знать не обязаны.
Вернёмся к наскальному рисунку.) Дойти до правильного ответа можно по такой цепочке:
1. Пунктир идёт на ось У. Значит, автора интересует синус угла!
2. Угол в первой четверти отпадает. Это явно угол из таблицы синусов и косинусов, автор его и так знает. Может быть...) Да и зачем тогда отмечен угол в четвёртой четверти!? Значит, автора интересует синус некоего угла из четвёртой четверти!
3. Отмеченные дужками углы, очевидно, должны быть равны... Угол в первой четверти всяко меньше 60°... Да и меньше 45°! Стало быть, это 30 градусов!
4. Угол в четвёртой четверти... Возможны 2 варианта... -30° и 330°. Но автора интересует положительный угол... Всё!!! На наскальном рисунке изображена попытка найти sin330°! Возможно, автор даже и определил его.)
sin330° = -0,5
Пора применить знания на практике. Потренироваться. Намекаю, что таблицу синусов и косинусов можно использовать только для проверки! Тонко так намекаю...) Предупреждаю, что никаких особых формул и тригонометрических преобразований здесь не требуется. Просто определяем значения и подставляем в пример. Чтобы горе от ума не получилось...)
Вычислить:
cos0° + sin90° - cos180° - sin270° =
sin135° · cos315° =
sin240° · cos330° =
cos(-120°) · sin(-330°) =
sin(-2430°) + cos(-1380°) =
Ответы (в беспорядке): 1,5; -0,25; 4; -0,75; 0,5
Получается? Отлично! Не получается? Путаница с отрицательными значениями? Бывает... Ничего страшного. Самое главное - правильно нарисовать (отсчитать) угол на круге. А там уже всё видно. Здесь вам поможет урок: Как нарисовать (отсчитать) любой угол на тригонометрическом круге в градусах.
Самые азы, конечно, но куда без них?)
Усложним задачу. Работаем по-взрослому. С радианами. Именно эта мера угла является основной в солидной математике.
Вычислить:





Ответы (в беспорядке): 0,5; 1,5; -2; -0,5; 0,25.
Что, с радианами сложнее, да? В градусы переводить, потом лишние обороты отбрасывать... Да, хлопотное занятие! Кстати, в этом уроке мы только с градусами работали, если кто заметил...) Это специально.
Только для тех, кто добрался до этих строк!)
Дело в том, что есть очень простой практический приём работы с радианами. Да такой приём, что работа с радианами становится проще, много проще работы с градусами! Поэтому я и не расписывал здесь примеры с радианами и переводом их в градусы. Лишнее это. Гораздо проще и надёжнее работать с радианами напрямую.
Этот практический приём описан в уроке: Как нарисовать (отсчитать) любой угол на тригонометрическом круге в радианах.
Подытожим тему. В этом уроке кто хотел, тот научился лихо крутить по кругу углы, откидывать полные обороты и легко определять необходимые значения таблицы синусов и косинусов без этой самой таблицы. Это солидный багаж для контрольных и экзаменов.
Но самое главное в этом уроке - тренировка в работе с тригонометрическим кругом. Определять значения таблицы синусов и косинусов можно и без круга. По формулам приведения, о которых мы ещё поговорим. Но любая формула тригонометрии применима в своей узкой области. А круг помогает во всей тригонометрии. Скажем, тригонометрические неравенства (а это задания уровня С!) решаются на 90% через круг, а оставшиеся 10% - с помощью круга. Круг лишним не бывает!) Освойте его, и тригонометрия будет дружить с вами.
|
|
|


