 |
Сложные процентные ставки наращения
|
|
|
|
Сложная процентная ставка наращения – это ставка, при которой база начисления является переменной, то есть проценты начисляются на проценты. Предположим, что мы имеем Р руб., которые можно инвестировать по процентной ставке наращения i. Через один год мы будем иметь P (1+ i) руб. Если повторить этот процесс, инвестировав всю сумму P (1+ i), то к концу второго года будем иметь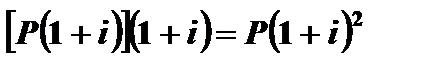 
. Продолжая процесс, видим, что показатель степени в формуле для наращенной суммы равен количеству лет наращения. Положив это число равным n, получим формулу сложных процентов.
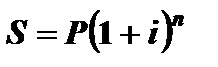(2.5)
Пример 2.3. Какой величины достигнет долг, равный 6000 руб., через 4 года при росте по сложной ставки наращения 18,5% годовых?
Решение. 
= 
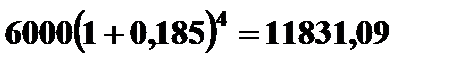руб.
При наращении по сложным процентам наращенная сумма быстро растет при увеличении числа лет. В табл. 2.1 представлен множитель наращения 
в зависимости от числа лет для двух значений ставки.
Таблица 2.1
| n, лет | i =10% | i =20% |
| 1,61 | 2,49 | |
| 2,594 | 6,192 | |
| 6,727 | 38,34 | |
| 117,4 | 9100,4 |
Если срок для начисления процентов является дробным числом, то для расчета наращенной суммы можно использовать как общий метод расчета по формуле (2.5), так и смешанный. При использовании смешанного метода дробное число лет представляется в виде суммы целого числа лет 
и его дробной части 
. Наращенная сумма в этом случае определяется формулой:
.
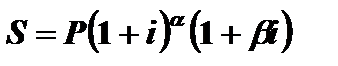Пример 2.4. Какой величины достигнет долг, равный 8000 руб. через 4,6 года при росте по сложной ставке наращения 20% годовых? Определить двумя методами.
Решение.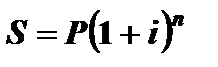 
= 
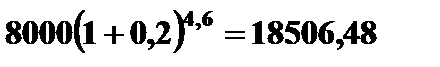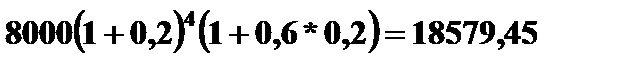руб.
= 
руб.
Часто в финансовых операциях в качестве периода наращения процентов используется не год, а, например, месяц, квартал или другой период. В этом случае говорят, что проценты начисляются m раз в году. При этом в контрактах фиксируется не ставка за период, а годовая ставка, которая в этом случае называется номинальной [6]. Сложная процентная ставка наращения является частным случаем номинальной при начислении процентов один раз в году. Если номинальную ставку обозначить через j, то проценты за один период начисляются по ставке j / m, а количество начислений равно mn. Наращенная сумма при использовании номинальной процентной ставки наращения определяется по формуле
|
|
|
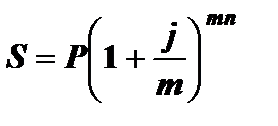(2.6)
Пример 2.5. Какой величины достигнет долг, равный 15000 руб. через 5,7 года при росте по сложной ставке 16,5% годовых при начислении процентов раз в году и помесячно?
Решение. 
= 
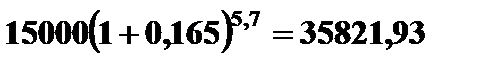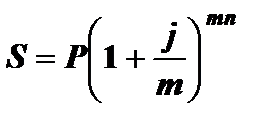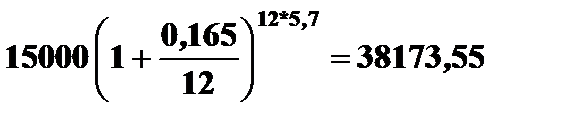руб.
= 
руб.
Если в формуле (2.6), определяющей наращенную сумму при использовании номинальной процентной ставки наращения, периоды начисления процентов постоянно уменьшать, то количество этих периодов в году будет увеличиваться. В пределе при стремлении длительности периодов к нулю их число стремится к бесконечности. Такое начисление процентов называется непрерывным, а процентная ставка при непрерывном начислении называется силойроста. Большое значение непрерывное наращение имеет в анализе сложных финансовых проблем, например, при анализе характеристик ценных бумаг.
Сила роста называется постоянной, если она не изменяется во времени. Если сила роста изменяется во времени, то она называется переменной.
Формула для наращенной суммы при непрерывном начислении процентов для постоянной силы роста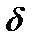 
следует из формулы (2.6) при стремлении m к бесконечности то есть
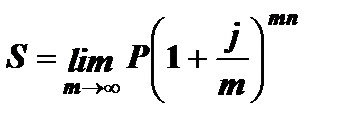
Так как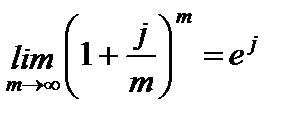 
, где e – число Эйлера (основание натуральных логарифмов), то, заменяя j на силу роста 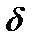, получим формулу для наращенной суммы при непрерывном начислении процентов:
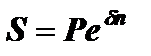(2.7)
Связь дискретных ставок i и j с силой роста 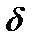находится из равенства множителей наращения дискретных (2.5), (2.6) и непрерывной (2.7) ставок, то есть
|
|
|
; 
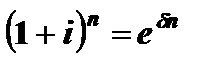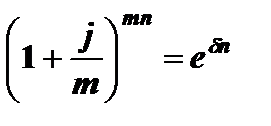
Решив эти уравнения, получим:
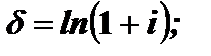
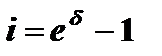(2.8)
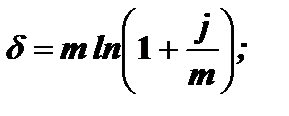
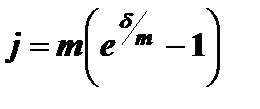(2.9)
По формулам (2.8) и (2.9) можно, в частности, зная дискретные ставки ценных бумаг, рассчитать силу роста этих бумаг.
Пример 2.6. На сумму 15000 руб. начисляются проценты по сложной годовой ставки i =22% в течении 3,5 лет. Определить силу роста и наращенную сумму при дискретном и непрерывном начислении.
Решение.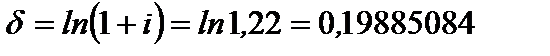 
или 19,885084%.
Наращенная сумма при непрерывном начислении
руб.
Наращенная сумма при дискретном начислении
руб.
Таким образом, как и следовало ожидать, наращенные суммы при дискретном и непрерывном начислениях совпали.
Пусть переменная сила роста изменяется во времени, то есть 
. В этом случае наращенная сумма определяется соотношением
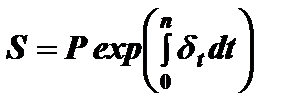
При дисконтировании суммы S, которая будет выдана через срок n, по ставке дисконтирования i вычисляется современная величина (стоимость) P суммы S. Используя формулы (2.3), (2.5), (2.6) и (2.7) получим соотношения дисконтирования для рассмотренных типов процентов
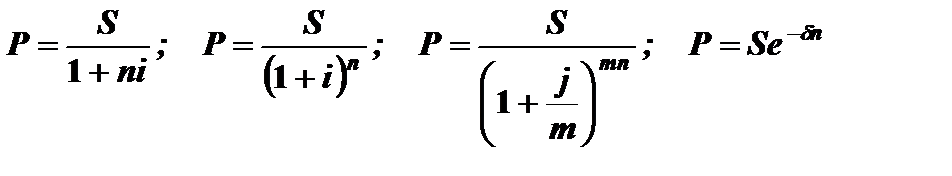(2.10)
Множители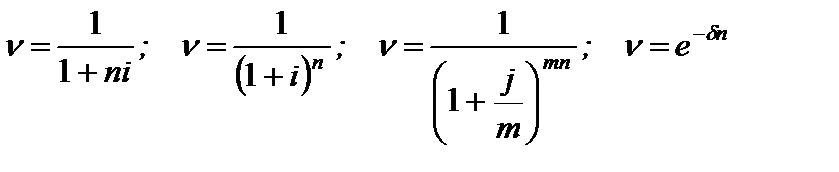 
называются дисконтными множителями.
Разность
D = S – P (2.11)
называется дисконтом с суммы S.
Пример 2.7. Через 159 дней должник уплатит 8,5 тыс. руб. Кредит выдан под простые проценты 19% годовых. Какова первоначальная сумма долга и дисконт при условии, что временная база равна 360 дней?
Решение.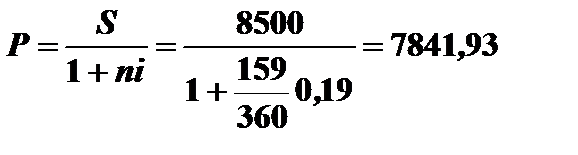 
руб.
D = S – P = 8500 – 7841,93 = 658,07 руб.
Пример 2.8. Построить таблицу для дисконтного множителя при сроке ссуды 5; 10; 20; 50 лет и при сложной ставке наращения 10% и 20%.
Решение. Результаты приведены в табл. 2.2.
Таблица 2.2
| n, лет | i =10% | i =20% |
| 0,621 | 0,402 | |
| 0,386 | 0,162 | |
| 0,149 | 0,026 | |
| 0,00852 | 0,00011 |
Пример 2.9. Сумма 12000 руб. выплачивается через 2,4 года. Номинальная ставка процентов – 16% годовых. Определить современную стоимость при ежеквартальном начислении процентов.
Решение.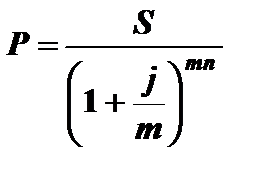 
= 
руб.
|
|
|
