Наилучшая структура капитала

Структура капитала предприятия определяется, как правило, отношением заемного и акционерного капитала. Иногда для этих целей используется коэффициент долговой нагрузки, являющейся отношением долга (текущие + долгосрочные долговые обязательства) к стоимости всех активов. Другим определением коэффициента долговой нагрузки является отношение долгосрочных обязательств к сумме долгосрочных обязательств и акционерного капитала. В общем случае дать рекомендации по выбору этих коэффициентов в виде одной цифры невозможно. В одних случаях бывает выгодно использовать заемный капитал, в других – акционерный. При выборе структуры капитала могут быть использованы четыре критерия, предложенные в [3].

1. Налоговая защита, уменьшающая стоимость займа за счет выплат по этому займу из налогооблагаемой прибыли. Займы дают преимущества тем фирмам, которые умеют и имеют возможность использовать налоговую защиту. Необходимо иметь в виду, что помимо выплат по займам налоговой защите подлежат и другие выплаты, например, амортизационные отчисления.

2. Деловой риск предприятия, при увеличении которого возможно возникновение финансовых трудностей, которые дорого обходятся и могут привести к банкротству. Поэтому фирмы с высоким деловым риском выпускают меньше долговых обязательств.

3. Ликвидность активов предприятия, показывающая насколько быстро и без потерь можно эти активы продать. Например, нематериальные активы при возникновении финансовых трудностей быстро теряют свою стоимость. Поэтому предприятия с высокой долей нематериальных активов делают меньше займов, чем предприятия, имеющие ликвидные активы и большой объем налогооблагаемой прибыли.

4.Финансовый заслон, обеспечивающий легкий доступ к финансам. Обычно финансовый заслон имеют те предприятия, которые обладают хорошими инвестиционными, технологическими и производственными решениями. Эффективность инвестиций этих предприятий высокая.

Приведенные критерии дают основания для принятия разумных решений об отношениях заемного и акционерного капитала.

В тех случаях, когда стоимость кредита увеличивается при увеличении объемов кредита, возможна оптимизация этих объемов. При этом можно указать такую долю заемного капитала по отношению к собственному, при котором норма прибыли на собственный капитал будет оптимальной (максимальной).

Пусть капитал предприятия формируется из собственного капитала и кредита. Доля собственного капитала равна , а доля кредита – . Доходность всего капитала предприятия обозначим , а стоимость кредита, которая в общем случае является функцией его доли , – . Причем

, (4.12)

Тогда норма прибыли на собственный капитал будет определяться соотношением

,

где C – собственный капитал, K – кредит, П = П_с + П_к – суммарная прибыль за год, состоящая из прибыли от собственного капитала и из прибыли от кредита , 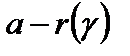– доходность по кредиту. Если весь капитал обозначить k, то 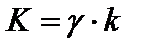, а . Тогда формула для нормы прибыли на собственный капитал приобретает вид

(4.13)

Взяв от нормы прибыли на собственный капитал (4.13) производную по и приравняв ее нулю, получим

(4.14)

(4.15)

Решив это уравнение относительно , получим ординату экстремальной точки.

Рассмотрим частный случай линейной зависимости стоимости кредита от доли кредита , имеющий вид

(4.16)

Подставив (4.16) в (4.15), получим

Пусть

(4.17)

Тогда

(4.18)

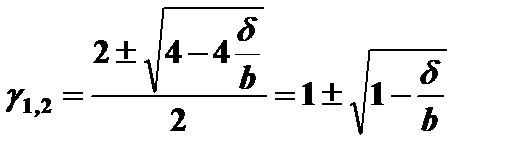
Первый корень не имеет финансового смысла, так как он лежит вне интервала . Поэтому оставляем решение

(4.19)

Поскольку значение под корнем должно быть положительным, то

(4.20)

Норма прибыли на собственный капитал (4.13) в экстремальной точке рассчитывается по формуле

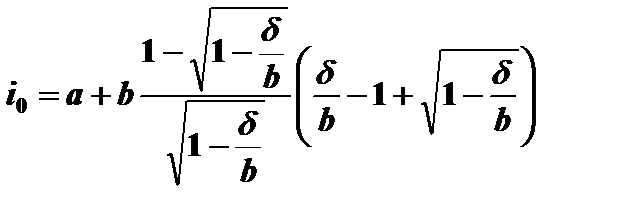
(4.21)

Функция нормы прибыли на собственный капитал для линейной стоимости кредита (4.16) приобретает вид

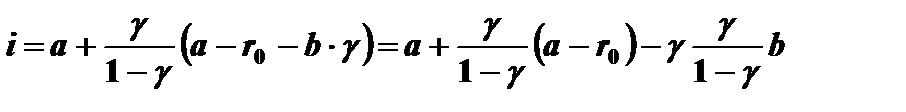(4.22)

Графики функци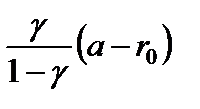й и при указанных ограничениях (4.12) и (4.29) и их разность представлены на рис. 4.1.

Координаты точки пересечения могут быть найдены из уравнения

= ; .

Рис. 4.1

Функция нормы прибыли на собственный капитал отличается от представленной на рис. 4.1 функции слагаемым . График функции от доли кредита представлен на рис. 4.2.

Рис. 4.2

Стоимость заемного капитала в оптимальной точке будет равна

(4.23)

Пример 4.5. Предприятие формирует свой капитал из собственного и заемного. Доходность по всему капиталу предприятия равна 25%. Собственный капитал предприятия составляет 100 млн. руб. Цена заемного капитала изменяется по линейному закону от его доли:

а) ,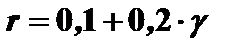

б) .

Определить оптимальную величину заемного капитала и его стоимость, а также оптимальную норму прибыли на собственный капитал.

Решение.

Вариант а) . По формуле (4.19) определяем оптимальное значение доли заемного капитала

Собственный капитал равен . Так как 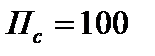млн. руб., то суммарный капитал =200 млн. руб.

Заемный капитал равен млн. руб.

Стоимость заемного капитала находим по формуле (4.23).

или 20%.

Оптимальная норма прибыли на собственный капитал определяется соотношением (4.21).

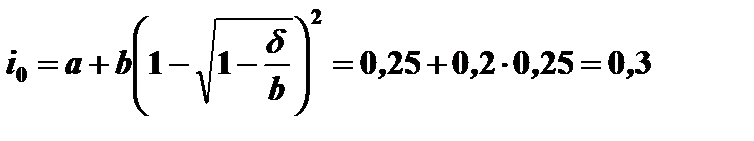или 30%.

Вариант б: . Так как для этого случая , а , то соотношение (4.20) не выполняется и оптимальное решение отсутствует.

В общем случае доходность всего капитала предприятия и стоимость кредита с учетом инфляции зависят от индекса цен за год 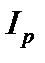. Помимо этого стоимость кредита зависит от налоговой защиты, определяемой ставкой налога на прибыль , и, как и прежде, от доли кредита . Если из налогооблагаемой прибыли выплачиваются только проценты, то стоимость кредита определяется соотношением

,

где – процентная ставка кредита, зависящая в общем случае от его доли .

При указанных параметрах чистая норма прибыли на собственный капитал будет определяться соотношением

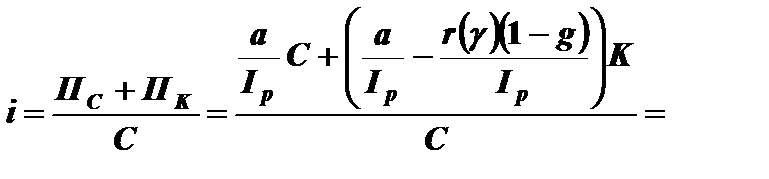
Причем

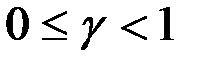, (4.24)

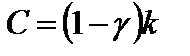Учитывая, что , а , получим

(4.25)

Производная по от функции (4.25) имеет вид

(4.26)

Приравняв производную (4.26) нулю, получим уравнение для определения абсцисс экстремальных точек

(4.27)

Отсюда следует, что абсцисса экстремальной точки не зависит от темпа инфляции.

Рассмотрим случай линейной зависимости стоимости кредита от доли кредита (4.16).

Подставив (4.25) в (4.36), получим

Введя обозначение (4.28) получим

(4.29)

По виду уравнение (4.37) совпало с уравнением (4.18). Как и прежде выбираем решение

(4.30)

Поскольку значение под корнем (4.30) должно быть положительным, то

(4.31)

Норма прибыли на собственный капитал (4.25) в экстремальной точке рассчитывается по формуле

 

(4.32)

Стоимость заемного капитала в оптимальной точке также определяется соотношением (4.23)

Пример 4.6. Предприятие формирует свой капитал из собственного и заемного. Доходность с учетом инфляции по всему капиталу предприятия равна 25%. Собственный капитал предприятия составляет 100 млн. руб. Цена заемного капитала изменяется по линейному закону от его доли , налог на прибыль равен 24%, а темп инфляции 30% в год.

Определить оптимальную величину заемного капитала и его стоимость, а также оптимальную норму прибыли на собственный капитал.

Решение. По формуле (4.28) находим

Оптимальное значение доли заемного капитала определим по формуле (4.30)

Из последней формулы следует, что , то есть соотношение (4.31) не выполняется и оптимальное решение отсутствует.

Пример 4.7. Предприятие формирует свой капитал из собственного и заемного. Доходность с учетом инфляции по всему капиталу предприятия равна 25%. Собственный капитал предприятия составляет 100 млн. руб. Цена заемного капитала изменяется по линейному закону от его доли , темп инфляции равен 30% в год.

Определить оптимальную величину заемного капитала и его стоимость, а также оптимальную норму прибыли на собственный капитал при:

а) наличии налоговой защиты и налоге на прибыль 24%,

б) отсутствии налоговой защиты.

Вариант а. Как и в предыдущем примере .

Оптимальное значение доли заемного капитала определим по формуле (4.30)

Собственный капитал равен . Так как млн. руб., то суммарный капитал =289359315,66 руб.

Заемный капитал равен ×289359315,66 = 189359315,66 руб.

Стоимость заемного капитала находим по формуле (4.23).

0,1 + 0,26×0,65440891449=0,2701463177.

Оптимальная норма прибыли на собственный капитал определяется соотношением (4.32).

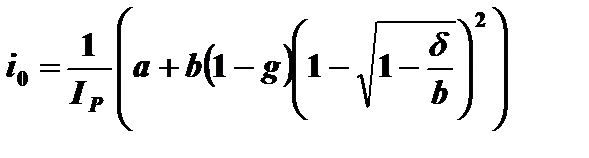= = 0,25740185.

Вариант б. По формуле (4.17) находим 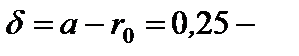0,1 = 0,15

Оптимальное значение доли заемного капитала

Собственный капитал равен . Так как млн. руб., то суммарный капитал =153741222,96 руб.

Заемный капитал равен

руб.

Стоимость заемного капитала

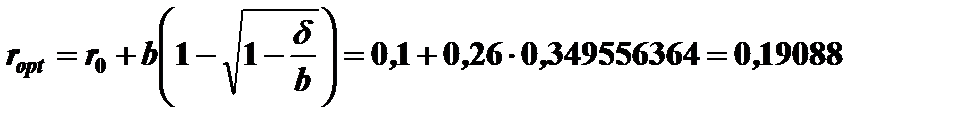
Оптимальная норма прибыли на собственный капитал

= 0,2167456

Как и следовало ожидать, в варианте а оптимальная норма прибыли на собственный капитал больше, чем в варианте б.

 

Контрольные вопросы

1.Дать определение стоимости капитала.

2.От каких параметров зависит стоимость капитала, полученного от обыкновенных акций?

3.От каких параметров зависит стоимость капитала, полученного от привилегированных акций?

4.Чем определяется стоимость вновь привлекаемого акционерного капитала?

5.Как связаны стоимость кредита и доходность по кредиту при расчете за кредит из чистой прибыли?

6.Что такое налоговая защита выплат по кредиту?

7.Чему равна стоимость кредита с ежегодными равными расходами по долгу при бесконечно большом сроке?

8.Как изменяется стоимость кредита с ежегодными равными расходами по долгу с конечным сроком по сравнению с кредитом, имеющем бесконечно большой срок?

9.Дать определение лизинга и показать его отличия от аренды.

10.Каковы преимущества лизинга для лизингодателя?

11.Каковы преимущества лизинга для лизингополучателя?

12.Дать определение финансового лизинга.

13.Дать определение операционного лизинга.

14.От чего зависит сумма разового платежа по лизингу?

15.Как связаны лизинговая годовая процентная ставка и ставка амортизации оборудования?

16.Как определяется доходность лизинговых операций?

17.На чем основан ответ на вопрос о покупке оборудования или лизинге?

18.Как определяется современная стоимость платежей по лизингу?

19.Как определяется современная стоимость платежей при покупке оборудования?

20.От чего зависит средневзвешенная стоимость капитала?

21.Как определяется наилучшая структура капитала?

 

 

Тема 5. ЭФФЕКТИВНОСТЬ РЕАЛЬНЫХ ИНВЕСТИЦИЙ
И МЕТОДЫ ЕЕ ОПРЕДЕЛЕНИЯ

Эффективность реальных инвестиций определяется путем анализа финансовых потоков инвестиционного проекта. Элементы финансовых потоков формируются из расходов и чистого дохода. Чистый доход – это выручка, полученная в каждом временном отрезке, за вычетом всех платежей, связанных с его созданием и получением (затраты на производство продукции (услуг), издержки предприятия, налоги).

Оценка эффективности инвестиционных проектов заключается в расчете системы показателей. Применяются, в основном, следующие показатели [2,6]:

- чистый приведенный доход (стоимость);

- период (срок) окупаемости;

- внутренняя норма доходности (рентабельности);

- индекс прибыльности (рентабельность).

Ставка дисконтирования

Для приведения доходов и расходов к одному моменту времени при оценке эффективности инвестиций используют ставку дисконтирования (сравнения). Выбор ставки сравнения существенным образом зависит от инфляции, риска, структуры капитала. Ставка дисконтирования должна быть не меньше стоимости капитала.

Ставка сравнения для собственного капитала определяется из следующих соображений. Безрисковая часть этой ставки 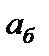определяется исходя из депозитного процента по вкладам без учета инфляции [9] или как доходность по безрисковым активам также без учета инфляции. За счет риска эта ставка увеличивается на величину (премия за риск). Выбор является весьма неопределенной задачей и зависит от степени риска проекта. Обычно премия за риск определяется экспериментально. В [17] приведены следующие рекомендации по выбору этой премии:

1) замещающие инвестиции:

- новые машины и оборудование, транспортные средства и т.д., которые будут выполнять те же функции, что и старое оборудование – =0%;

- новые машины и оборудование, которые заменяют старое оборудование, но являются более совершенными, требуют более высокой квалификации работников, других производственных подходов и т.д. – =3%;

- новые мощности, замещающие старые, новые заводы на том же или другом месте – =6%;

2) новые инвестиции:

- новые мощности или связанное оборудование, с помощью которого будут производится или продаваться те продукты, которые уже производились – 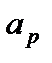=5%;

- новые мощности или машины для производства или продажи производственных линий, которые тесно связаны с существующими производственными линиями – =8%;

- новые мощности или машины, а также поглощение (приобретение) других форм для производства или продажи производственных линий, которые не связаны с первоначальной стоимостью компании – =15%;

3) инвестиции в НИР:

- прикладные НИР, направленные на определенные специфические цели – =10%;

- фундаментальные исследования, цели которых пока точно не определены и результат точно не известен – =20%.

Таким образом, ставка сравнения 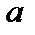для собственного капитала без учета инфляции находится из соотношения

Отсюда получим

Если и , то ставка сравнения для собственного капитала может быть рассчитана по формуле

При учете инфляции среднее значение ставки сравнения определяется соотношением

(5.1)

где – индекс цен за исследуемой период, состоящей из n элементарных периодов, t – номер элементарного периода, 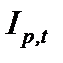– индекс цен за время элементарного периода под номером t, – темп инфляции за время элементарного периода под номером t. Таким образом, имея и задавшись , находят и . Из (5.1) следует, что при изменяющемся во времени темпе инфляции ставка сравнения также изменяется во времени. Поэтому выбор этой ставки постоянной на все время действия проекта является недостаточно правомерным.

Если весь капитал является заемным, то при выплатах по кредиту из чистой прибыли ставка сравнения приравнивается ставке кредита. В случае, когда выплаты по задолженности вычитаются из налогооблагаемой прибыли, то стоимость заемного капитала необходимо скорректировать (см. раздел 4.2). Например, если ставка по задолженности равна , а ставка налога на прибыль – , то эффективная ставка по задолженности при очень большом сроке кредита .

При смешенном капитале ставка сравнения может быть найдена как средневзвешенная стоимость этого капитала [9], рассчитанная с учетом инфляции

где – доля капитала, полученного из источника – стоимость капитала из источника ; m -общее количество источников. Здесь в общем случае будет изменятся во времени в зависимости от инфляции и конъюнктуры рынка.

5.2. Чистый приведенный доход
(Net Present Value – NPV)

Чистый приведенный доход W – это разность доходов и расходов, дисконтированных на начало инвестиционного процесса. Если процесс отдачи идет сразу после окончания инвестиций, то формула для расчета чистого приведенного дохода имеет вид

(5.2)

где – инвестиционные расходы в периоде ; 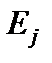-доходы в периоде ; – продолжительность процесса инвестиций; – продолжительность процесса отдачи от инвестиций, – ставка сравнения. Следует обратить внимание на то, что после окончания инвестиций нумерация периодов процесса отдачи начинается с единицы.

Если чистый приведенный доход больше нуля, то проект принимается для дальнейшего рассмотрения, если меньше, то отвергается.

Пример 5.1. Имеются два варианта инвестиционного проекта, в которых платежи постнумерандо распределены по годам следующим образом:

проект 1 -2 -4 4 4 5

проект 2 -3 -3 4 5 6

Сравнить проекты по чистому приведенному доходу при ставке сравнения q =10%.

Решение. ,

.

Так как , то второй проект предпочтительнее первого.

Если установлены закономерности поведения финансовых потоков во времени, то появляется возможность развернутого анализа различных факторов и их влияния на эффективность проектов. Например, для платежей и поступлений в виде р- срочной ренты и при начислении процентов один раз в году формула для расчета чистого приведенного дохода приобретает вид

, (5.3)

где , – ежегодные поступления и затраты соответственно. В формуле (5.3) из современной величины отсроченной ренты (доход) вычитается современная величина немедленной ренты (инвестиции).

Пример 5.2. Инвестиции производятся по полугодиям по 100 млн. руб. в год в течение 3 лет. Ожидаемая поквартальная отдача – 20 млн. руб. в квартал в течение 12 лет. Ставка сравнения 10%. Определить чистый приведенный доход.

Решение. В приведенных выше обозначениях условие задачи можно записать в виде

Тогда .

Подставив полученные значения в (5.3), найдем

млн. руб.

Ставка сравнения 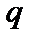является в определенном смысле величиной условной. Поэтому чистый приведенный доход определяется для некоторого диапазона этих ставок. Возможная зависимость чистого приведенного дохода от ставки сравнения приведена на рис. 5.1. Из рисунка следует, что чистый приведенный доход может быть как положительной, так и отрицательной величиной.

Рис. 5.1.

При высоком уровне ставки сравнения отдаленные платежи оказывают малое влияние на чистый приведенный доход. Поэтому различные по продолжительности варианты могут оказаться практически равноценными. С другой стороны считают, что проект с более длительным поступлением доходов, при прочих равных условиях, предпочтительнее. Это вызывает попытки пересмотра рассмотренной выше методики расчета чистого приведенного дохода. Например, те поступления, которые охватываются сроком окупаемости, дисконтируются и рассматриваются, как покрытие инвестиций. На остальные поступления дисконтирование не распространяется. Такие подходы иногда используются, несмотря на трудности их экономического обоснования.

Скорректированный чистый приведенный доход складывается из базового чистого приведенного дохода, рассмотренного выше, и издержек или выгод приведенных стоимостей побочных эффектов проекта, к которым, например, относятся расходы на эмиссию ценных бумаг, налоговая защита по процентным платежам (проценты по долгу вычисляются из налогооблагаемой прибыли), особое финансирование (например, правительство может предложить субсидии для проектов, имеющих общественную значимость).

5.3. Индекс прибыльности
(Profitability Index – PI)

Индексом прибыльности (рентабельностью) называется отношение приведенных доходов к приведенным на ту же дату инвестиционным расходам.

, (5.4)

В этой формуле использовались те же обозначения, что и в формуле (5.2).

Пример 5.3. Имеются два варианта инвестиционного проекта, в которых платежи постнумерандо распределены по годам следующим образом:

проект 1 -2 -4 4 4 5

проект 2 -3 -3 4 5 6

Сравнить проекты по индексу прибыльности при ставке сравнения q =10%.

Решение. Проект 1.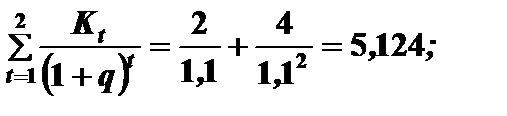

.

Проект 2.

.

Так как U ₂ > U ₁, то второй проект предпочтительнее первого.

Для платежей и поступлений в виде р -срочной ренты и при начислении процентов один раз в году формула для расчета рентабельности приобретает вид

, (5.5)

где .

Здесь современная величина отсроченной ренты (доход) делится на современную величину немедленной ренты (инвестиции).

Пример 5.4. Инвестиции производятся по полугодиям по 50 млн. руб. за полгода в течение 3 лет. Ожидаемая отдача – 80 млн. руб. в год в течение 12 лет при поквартальных выплатах. Ставка сравнения 10%. Определить рентабельность.

Решение.

= =80*7,064*0,7513 =424,577

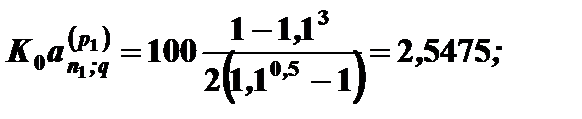
5.4. Внутренняя норма доходности
(Internal Rate of Return – IRR)

Внутренняя норма доходности – это расчетная процентная ставка, при которой чистая приведенная стоимость равна нулю, то есть приведенные доходы равны приведенным расходам. На рис. 5.1 внутренняя норма доходности равна координате q_в точки пересечения кривой с осью q.

В общем случае внутренняя норма доходности q_в находится путем решения уравнения

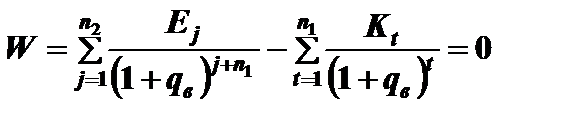(5.6)

Обозначения величин в формуле (5.6) приведены в разделе 5.2. Чем выше внутренняя норма доходности, тем больше эффективность капиталовложений. Если издержки проекта меньше, чем внутренняя норма доходности, то чистая приведенная стоимость является положительной и инвестиционный проект следует принять. При их равенстве проект имеет нулевую чистую приведенную стоимость.

Внутренняя норма доходности полностью определяется внутренними характеристиками проекта. Для дальнейших исследований обычно отбираются те проекты, внутренняя норма доходности которых превышает 15–20% при темпе инфляции 4–5% в год.

Пример 5.7. Имеются два варианта инвестиционного проекта, в которых платежи постнумерандо распределены по годам следующим образом:

проект 1 -2 -4 4 4 5

проект 2 -3 -3 4 5 6

Сравнить проекты по внутренней норме доходности.

Решение. Для решения уравнения (5.6) воспользуемся методом Ньютона-Рафсона. Введя обозначение 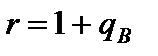, перепишем (5.6) в виде 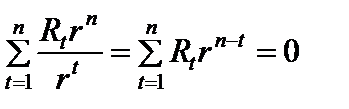. Положим . Тогда , так как . Положим .

Проект 1

Итерация 1. ;

;

.

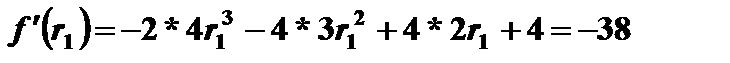Итерация 2. ;

; .

Прежде, чем переходить к следующей итерации, проведем проверку, подставив полученный результат в (5.6).

. В идеале этот результат должен быть равен нулю. Так как результат невелик, то можно прекратить вычисления и принять q_В ==39,29%

Проект 2

Итерация 1

Итерация 2

Проверка:

Принимаем q_В =43,036%.

Таким образом, второй проект предпочтительнее первого.

Убывающая функция чистого приведенного дохода от ставки сравнения (рис. 5.1) далеко не всегда имеет место. Если, например, ранние платежи положительны, а поздние отрицательны, то функция чистого приведенного дохода может возрастать при увеличении ставки сравнения. В общем случае функция чистого приведенного дохода от ставки сравнения может несколько раз пересекаться с осью . В таких случаях использование этого показателя для оценки проектов становится весьма проблематичным.

5.5. Период окупаемости
(Payback Period – PBP)

Период (срок) окупаемости – это временной интервал, в течении которого сумма чистых доходов, дисконтированных на момент завершения инвестиций, равна сумме инвестиций, приведенных к тому же моменту времени.

При определении периода окупаемости находят сумму инвестиций К, приведенных к моменту их завершения, по формуле

Затем, используя соотношение 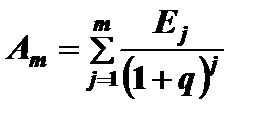, определяют значение m+1, для которого удовлетворяется неравенство

(5.7)

Период окупаемости лежит между концом периода под номером m и концом периода под номером m+1, отсчитываемых после окончания инвестиций. Метод определения недостающей части периода поясняется на рис. 5.2 (принимается, что поступления изменяются по линейному закону).

Рис. 5.2.

Из подобия треугольников находим 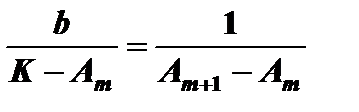. Откуда

(5.8)

Пример 5.5. Имеются два варианта инвестиционного проекта, в которых платежи постнумерандо распределены по годам следующим образом:

проект 1 -2 -4 4 4 5

проект 2 -3 -3 4 5 6

Сравнить проекты по периоду окупаемости при ставке сравнения q =10%.

Решение. Для проекта 1 сумма инвестиций, приведенная к их окончанию, равна К=2(1+0,1)+4=6,2.

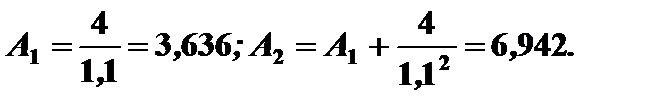Таким образом, срок окупаемости лежит между первым и вторым годом после окончания инвестирования. Используя (5.8), находим срок окупаемости

лет.

Для проекта 2. К =3(1+0,1)+3=6,3; ;

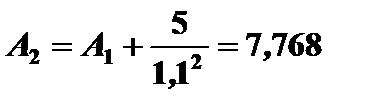; лет.

По периоду окупаемости второй проект предпочтительнее первого.

Для р -срочной ренты при начислении процентов один раз в году срок окупаемости рассчитывается по формуле

, (5.9)

где A – затраты, приведенные к окончанию инвестиций; Е ₀ – отдача от инвестиций за год; р – количество поступлений дохода в течение года.

Пример 5.6. Инвестиции производятся по полугодиям по 50 млн. руб. за полгода в течение 3 лет. Ожидаемая поквартальная отдача – 20 млн. руб. в квартал. Ставка сравнения 10%. Определить срок окупаемости.

Решение. Затраты, приведенные к окончанию инвестиций, вычисляются по формуле

,

где =50*2=100; ; . Подставив значение для А, а также 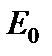=20*4=80 и 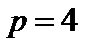в формулу (5.8), получим

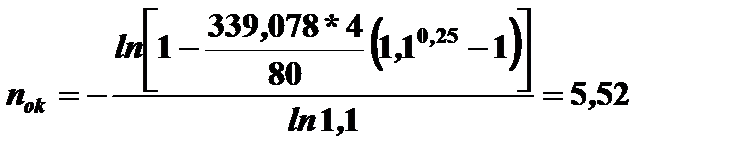года.

Период окупаемости не учитывает весь срок функционирования проекта. На него не влияет отдача, лежащая за пределами этого срока. Это является основным недостатком рассматриваемого показателя. Наиболее сильно этот недостаток проявляется при неравномерных денежных потоках. Поэтому срок окупаемости не служит критерием выбора проекта, а используется лишь в виде ограничения при принятии решения.

⇐ Предыдущая234567891011Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: