 |
Финансовая эквивалентность обязательств
|
|
|
|
В практической деятельности довольно часто возникают ситуации, когда один поток платежей заменяется другим потоком или одним платежом. При этом соблюдается неизменность финансовых отношений сторон до и после заключения контракта или, как говорят, финансовая эквивалентность обязательств. Расчет платежей в этом случае базируется на уравнении эквивалентности.
Уравнением эквивалентности является равенство сумм заменяемых и заменяющих платежей, приведенных к одному моменту времени.
Принцип финансовой эквивалентности обязательств позволяет, в частности, сравнивать два отдельных платежа, выплачиваемые в различные моменты времени. При этом используются простые проценты, если сроки платежей меньше года, и сложные проценты – если сроки больше года.
Пусть имеются два платежа 
и 
со сроками соответственно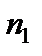 
и 
. При оценке этих платежей сравниваются их современные стоимости, и тот платеж считается большим, у которого больше его современная стоимость. Иногда возникает необходимость в определении критической ставки 
, при которой два рассматриваемых платежа оказываются равными. Рассмотрим два варианта.
1. Для простых процентов критическая ставка находится из уравнения эквивалентности, получаемого путем приравнивания современных стоимостей первого и второго платежей
Решая это уравнение относительно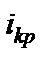 
, найдем
Пример 3.15. Первый платеж, равный 900 руб., должен быть выплачен через 30 дней, а второй, равный 920 руб., выплачивается через 270 дней. Сравнить эти платежи при простой процентной ставке 15% годовых и при базе К =360.
Решение. Современная стоимость первого платежа
руб.
Современная стоимость второго платежа
руб.
|
|
|
При заданной ставке первый платеж превышает второй.
Пример 3.16. Первый платеж, равный 900 руб., должен быть выплачен через 30 дней, а второй, равный 920 руб., выплачивается через 270 дней. Определить критическую ставку при базе К=360.
Решение. Критическая ставка, при которой платежи эквивалентны, определяется по формуле
или 3,34%.
2.Для сложных процентов уравнение эквивалентности имеет вид
Решая это уравнение относительно 
, найдем
Пример 3.17. Первый платеж, равный 9 тыс. руб., должен быть выплачен через 2 года, а второй, равный 12 тыс. руб., выплачивается через 5 лет. Сравнить эти платежи при сложной процентной ставке 15% годовых.
Решение. Современная стоимость первого платежа
руб.
Современная стоимость второго платежа
руб.
При заданной ставке первый платеж превышает второй.
Пример 3.18. Первый платеж, равный 9 тыс. руб., должен быть выплачен через 2 года, а второй, равный 12 тыс. руб., выплачивается через 5 лет. Определить критическую ставку.
Решение. Критическая ставка, при которой платежи эквивалентны, определяется по формуле
или 10,06%.
Объединение потока платежей в один называется также консолидацией платежей. При этом определяют либо сумму консолидированного платежа при известном сроке, либо срок при известной сумме. Рассмотрим вначале задачу определения суммы консолидированного платежа при известном сроке. Эта задача может быть сформулирована следующим образом: пусть платежи с номерами 1, 2,..., m и со сроками, прономерованными соответственно, заменяются одним в сумме 
с известным сроком 
. Определить 
. В общем случае срок 
может лежать между первой и последней выплатами заменяемых платежей. Cхема выплат может быть представлена так, как показано на рис. 3.7.
S 1 S 2 St ST S 0 S 1 S 2 Sk SK
0 n 1 n 2 nt nT n 0 n 1 n 2 nk nK n
Рис.3.7.
Здесь всем платежам до момента n 0 присвоен номер t ивсего таких платежей Т, а платежам после момента n 0 присвоен номер k ивсего таких платежей K. Общее количество заменяемых платежей m = T + K. Сумма консолидированного платежа при начислении простых процентов определяется по формуле
|
|
|
В первую сумму входят все наращенные платежи со сроками меньше срока консолидированного платежа, а во вторую сумму входят все дисконтированные платежи со сроками больше срока консолидированного платежа. Если срок консолидированного платежа наступит позже последнего срока заменяемых платежей, то эта формула приобретает вид
Пример 3.19. Три платежа 5 тыс. руб. со сроком 130 дней, 3 тыс. руб. со сроком 165 дней и 8 тыс. руб. со сроком 320 дней заменяются одним со сроком 250 дней. Стороны договорились об использовании простой процентной ставки 20% годовых. Определить сумму консолидированного платежа при базе К =365.
Решение. Схема выплат представлена на рис. 3.8.
5000 3000 S 0 8000 S, руб.
0 130 165 250 320 n, дней
Рис. 3.8.
При определении суммы консолидированного платежа используется рис. 3.8.
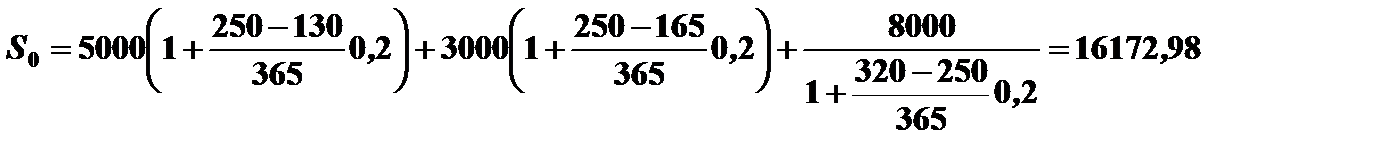
Сумма консолидированного платежа при начислении сложных процентов определяется по формуле
Если срок консолидированного платежа наступит позже последнего срока заменяемых платежей, то эта формула приобретает вид
Пример 3.20. Три платежа 5 тыс. руб. со сроком 2 года, 4 тыс. руб. со сроком 4 года и 6 тыс. руб. со сроком 5 лет заменяются одним со сроком 3 года. Стороны договорились об использовании сложной процентной ставки 25% годовых. Определить сумму консолидированного платежа.
Решение. Схема выплат представлена на рис. 3.9.
При определении суммы консолидированного платежа используется рис. 3.9.
5000 S 0 4000 6000 S, руб.
0 2 3 4 5 n, лет
Рис. 3.9.
руб.
При определении срока консолидированного платежа уравнение эквивалентности представляют как равенство современных стоимостей заменяемых и консолидированного платежей. В этом случае схема выплат может быть представлена так, как показано на рис. 3.10.
S 1 S 2 Sj S 0 Sm
0 n 1 n 2 nj n 0 nm n
Рис. 3.10
В соответствии с обозначениями рис. 3.10 уравнение эквивалентности для простых процентов имеет вид
Сумму в правой части этого уравнения обозначим буквой U, то есть
Тогда решение уравнения эквивалентности относительно имеет вид
Пример 3.21. Три платежа 8 тыс. руб. со сроком 130 дней, 10 тыс. руб. со сроком 160 дней и 4 тыс. руб. со сроком 200 дней заменяются одним в размере 21 тыс. руб. Стороны договорились об использовании простой процентной ставки 20% годовых. Определить срок консолидированного платежа при базе К =365.
|
|
|
Решение. Схема выплат представлена на рис. 3.11.
21000 8000 10000 4000 S, руб.
0 n 0 130 165 200 n, дней
Рис. 3.11.
При определении современной стоимости заменяемых платежей используется рис. 3.11.
Срок консолидированного платежа находится по формуле
года.
Определим срок в днях по формуле
дней.
В соответствии с обозначениями рис. 3.11 уравнение эквивалентности для сложных процентов имеет вид
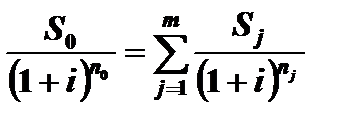
Сумму в правой части этого уравнения обозначим буквой U, то есть
Тогда уравнения эквивалентности можно записать в виде
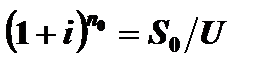
Прологарифмировав левую и правую части этого уравнения, найдем
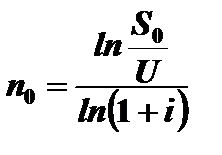
Пример 3.22. Три платежа 2 тыс. руб. со сроком 2 года, 4 тыс. руб. со сроком 3 года и 3 тыс. руб. со сроком 4 года заменяются одним в размере 8 тыс. руб. Стороны договорились об использовании сложной процентной ставки 18% годовых. Определить срок консолидированного платежа.
Решение. Схема выплат представлена на рис. 3.12.
2000 4000 3000 8000 S, руб.
0 2 3 4 n 0 n, лет
Рис. 3.12.
При определении современной стоимости заменяемых платежей используется рис. 3.12.
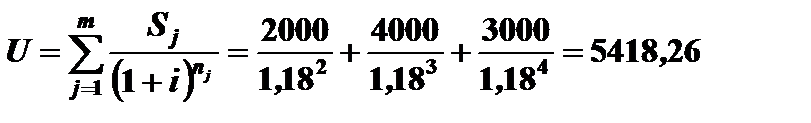руб.
Срок консолидированного платежа находится по формуле
года или 2 года 129 дней.
Контрольные вопросы
1.Какие потоки платежей называются регулярными?
2.Дать определение наращенной суммы и современной стоимости потока платежей.
3.Какие ренты называются постоянными?
4.Дать определение годовой ренты, ренты с начислением процентов по номинальной процентной ставки, р – срочной ренты, непрерывной ренты.
5.Как изменяются наращенная сумма и современная стоимость ренты пренумерандо по сравнению с рентой постнумерандо?
6.Написать формулу для современной стоимости вечной ренты.
7.Описать метод расчета величины годовой выплаты ренты.
8. Описать метод расчета срока ренты.
9.Описать метод расчета процентной ставки ренты.
10.Что такое финансовая эквивалентность обязательств?
|
|
|
11.Дать определение уравнения эквивалентности.
12.Описать принцип расчета суммы консолидированного платежа при использовании простой и сложной процентных ставок.
13.Описать принцип расчета срока выплаты консолидированного платежа.
|
|
|
