 |
Определение параметров рент
|
|
|
|
При определении величины годовой выплаты ренты используются полученные выше формулы для расчета наращенной суммы и современной стоимости различных рент. При этом должны быть заданы все параметры ренты кроме годовой выплаты. Для р – срочной ренты с начислением процентов m – раз в году величина годовой выплаты определяется по формулам (3.9) и (3.11).
; 
, (3.30)
где S и A наращенная сумма и современная стоимость ренты соответственно, 
и 
– коэффициенты наращения и приведения ренты соответственно, p – количество выплат в году, m – количество начислений процентов в году, j – номинальная процентная ставка, n – срок ренты в годах.
Пример 3.12. В фонд ежегодно в конце периода поступают средства в течении семи лет, на которые начисляются проценты по ставке 15% годовых, причем выплаты производятся поквартально, а проценты начисляются ежемесячно (раз в году). Наращенная сумма к концу срока составит 100 тыс. руб. Определить коэффициент наращения ренты и годовую выплату.
Решение. Коэффициент наращения ренты при поквартальных выплатах и начислении процентов ежемесячно находится по формуле (3.10).
= 
Коэффициент наращения ренты при поквартальных выплатах и начислении процентов раз в году (m =1) определяется формулой
Годовые выплаты при начислении процентов ежемесячно составят
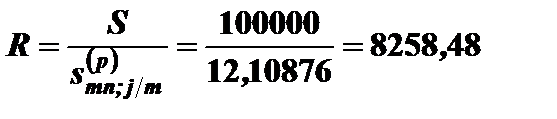руб.
Годовые выплаты при начислении процентов раз в году
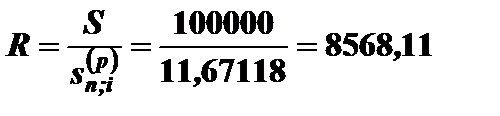руб.
Для других типов рент величина годовой выплаты определяется аналогично.
В практической деятельности возникают задачи определения срока ренты при прочих известных параметрах. Срок ренты определяется из формул для наращенной суммы и современной стоимости ренты, которые получены нами раньше. Наиболее общим случаем постоянной ренты является рента с начислением процентов по номинальной процентной ставке и с неоднократными выплатами в году. Для этой ренты наращенная сумма определяется по формуле
|
|
|
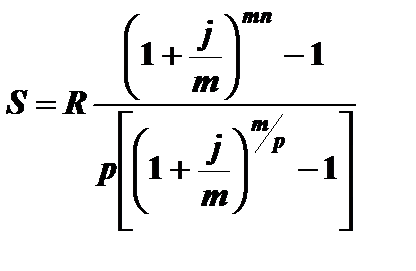
Представим эту формулу в виде
Прологарифмировав правую и левую части этого равенства, получим
Решив это уравнение относительно n, окончательно получим
(3.31)
При расчете по этой формуле срок получается, как правило, дробным. Поэтому количество периодов np округляется до целого числа. Затем уточняется значение разового платежа по формуле
(3.32)
Пример 3.17. В фонд поступают средства, на которые начисляются проценты по ставке 15% годовых, причем выплаты производятся в конце каждого квартала, а проценты начисляются ежемесячно. Величина фонда на конец срока составит 100 тыс. руб., годовая выплата – 10 тыс. руб. Определить срок ренты.
Решение. Срок ренты находится по формуле (3.36).
=
лет.
Количество кварталов в полученном сроке составит np =6,197*4=24,788. Округляем полученное число до 25, то есть количество лет ренты принимается равным 6,25. Подставив это число в формулу (3.37), получим величину ежеквартальной выплаты.
руб.
Аналогично находят формулу для срока ренты с начислением процентов по номинальной процентной ставке и с неоднократными выплатами в году по ее современной стоимости. Эта формула имеет вид
(3.33)
Формула для уточнения значения разового платежа
(3.34)
Пример 3.13. Долг в размере 50 тыс. руб. погашается равными частями в конце каждого квартала по 2,5 тыс. руб. На взносы начисляются проценты раз в году по ставке 15% годовых. Определить время погашения долга.
Решение. Срок ренты находится по формуле (3.33), которая для условий примера принимает вид
=
8,886 лет.
Количество кварталов в полученном сроке составит np =8,886*4=35,5. Округляем полученное число до 35, то есть количество лет ренты принимается равным 8,75. Подставив это число в формулу (3.34), уточним величину ежеквартальной выплаты.
|
|
|
руб.
Для других типов ренты срок находится аналогично.
Важной проблемой при анализе потоков платежей является задача расчета процентной ставки ренты. Если известны все параметры ренты кроме процентной ставки, то расчет процентной ставки можно трактовать как определение доходности финансовой операции. Процентная ставка определяется из соотношений для расчета наращенной суммы и современной стоимости по формулам, полученным выше, для различных типов рент. В отличие от определения годовой выплаты ренты или ее срока, выражение для расчета процентной ставки, как правило, нельзя представить в виде формулы. Поэтому процентную ставку ренты рассчитывают цифровыми способами. Рассмотрим один из способов, называемый методом Ньютона-Рафсона.
В общем случае метод Ньютона-Рафсона состоит в последовательном приближении к решению 
нелинейного уравнения 
. Геометрический смысл метода поясняется на рис. 3.6.
Предполагается, что функция 
в исследуемой области является гладкой, непрерывной, монотонно возрастающей или монотонно убывающей. Вблизи решения 
выбирается произвольная точка 
. Через точку (
, 
) проводится касательная к функции 
, которая пересекается с осью 0 
в точке 
. Как следует из рис. 3.6, эта точка лежит ближе к решению 
по сравнению с точкой 
. Координата точки 
определяется из геометрии рис. 3.6. Из прямоугольного треугольника следует, что
(3.35)
Рис. 3.6.
Так как tga является производной f' (x 1) функции f (x) в точке x 1, то решение (3.35) относительно x 2 можно записать в виде
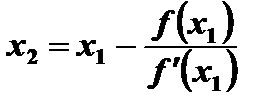
Аналогично находится координата точки x 3 еще ближе лежащей к решению x 0. В общем случае рекуррентное соотношение можно представить в виде
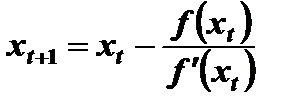, (3.36)
где t – номер итерации.
Для годовой ренты наращенная сумма определяется формулой (3.4), которую перепишем в виде
(3.37)
При решении этого уравнения его приводят к виду, удобному для дальнейших расчетов. Прежде всего введем замену
(3.38)
и перенесем левую часть вправо. В результате получим
Так как на ноль делить нельзя, то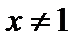 
.
Умножив левую и правую части этого уравнения на 
, найдем
В качестве искомой функции принимаем
(3.39)
Производная этой функции вычисляется по формуле
|
|
|
(3.40)
Пример 3.14. В накопительный фонд ежегодно в конце года поступают средства по 10 тыс. руб. в течении 7 лет, причем на конец срока величина фонда составит 100 тыс. руб. Определить доходность инвестиций.
Решение. Для решения используются формулы (3.36),(3.39) и (3.40). 
. Положим =1,15.
Первая итерация. 
;
;
.
Вторая итерация. 
; 
;
Третья итерация. 
; 
.
Поскольку результаты во второй и в третьей итерациях слабо отличаются друг от друга, то вычисления можно прекратить и принять в соответствии с (3.43) 
или 11,71235%. Другим методом, подтверждающим окончание вычислений, является проверка. Для этого в правую часть уравнения (3.37) подставляют полученное значение ставки. Если результат совпадает с левой частью или слабо отличается от нее, то вычисления прекращаются. Для рассматриваемого примера
Поскольку результаты практически совпали, так как 
, то принимаем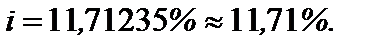 
|
|
|
