Частная теорема о повторении опытов

При практическом применении теории вероятностей часто приходится встречаться с задачами, в которых один и тот же опыт или аналогичные опыты повторяются неоднократно. В результате каждого опыта может появиться или не появиться некоторое событие , причем нас интересует не результат каждого отдельного опыта, а общее число появлений события в результате серии опытов. Например, если производится группа выстрелов по одной и той же цели, нас, как правило, интересует не результат каждого выстрела, а общее число попаданий. В подобных задачах требуется уметь определять вероятность любого заданного числа появлений события в результате серии опытов. Такие задачи и будут рассмотрены в данной главе. Они решаются весьма просто в случае, когда опыты являются независимыми.

Несколько опытов называются независимыми, если вероятность того или иного исхода каждого из опытов не зависит от того, какие исходы имели другие опыты. Например, несколько последовательных бросаний монеты представляют собой независимые опыты. Несколько последовательных выниманий карты из колоды представляют собой независимые опыты при условии, что вынутая карта каждый раз возвращается в колоду и карты перемешиваются; в противном случае это – зависимые опыты. Несколько выстрелов представляют собой независимые опыты только в случае, если прицеливание производится заново перед каждым выстрелом; в случае, когда прицеливание производится один раз перед всей стрельбой или непрерывно осуществляется в процессе стрельбы (стрельба очередью, бомбометание серией), выстрелы представляют собой зависимые опыты. Независимые опыты могут производиться в одинаковых или различных условиях. В первом случае вероятностьсобытия от опыта к опыту меняется. К первому случаю относится частная теорема, а ко второму – общаятеорема о повторении опытов. Мы начнем с частной теоремы, как более элементарной. Прежде всего, рассмотрим конкретный пример.

Пример. Производится три независимых выстрела по мишени, вероятность попадания в которую при каждом выстреле равна . Найти вероятность того, что при этих трех выстрелах мы получим ровно два попадания.

Решение. Обозначим событие, состоящее в том, что в мишень попадет ровно два снаряда. Это событие может произойти тремя способами:

1) попадание при первом выстреле, попадание при втором, промах при третьем;

2) попадание при первом выстреле, промах при втором, попадание при третьем;

3) промах при первом выстреле, попадание при втором, попадание при третьем.

Следовательно, событие можно представить как сумму произведений событий:

,

где - попадания при первом, втором, третьем выстрелах соответственно, - промах при первом, втором, третьем выстрелах.

Учитывая, что три перечисленных варианта события несовместны, а события, входящие в произведения, независимы, по теоремам сложения и умножения получим:

,

или, обозначая ,

.

Аналогичным образом, перечисляя все возможные варианты, в которых интересующее нас событие может появиться заданное число раз, можно решить и следующую общую задачу.

Производится независимых опытов, в каждом из которых может появиться или не появится некоторое событие ; вероятность появления события в каждом опыте равна , а вероятность непоявления 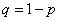. Требуется найти вероятность того, что событие в этих опытах появится ровно раз.

Рассмотрим событие , состоящее в том, что событие появится в опытах ровно раз. Это событие может осуществиться различными способами. Разложим событие на сумму произведений событий, состоящих в появлении или непоявлении события в отдельном опыте. Будем обозначать появление события в i-м опыте; - непоявление события в i-м опыте.

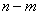Очевидно, каждый вариант появления события (каждый член суммы) должен состоять из m появлений события и непоявлений, т.е. из событий и 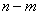событий 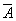с различными индексами. Таким образом,

причем в каждое произведение событие должно входить раз, а 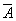должно входить 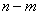раз.

Число всех комбинаций такого рода равно , т.е. числу способов, какими можно из опытов выбрать , в которых произошло событие . Вероятность каждой такой комбинации, по теореме умножения для независимых событий, равна . Так как комбинации между собой несовместны, то, по теореме сложения,вероятность события равна

Таким образом, мы можем дать следующую формулировку частной теоремы о повторении опытов.

Если производится независимых опытов, в каждом из которых событие появляется с вероятностью , товероятность того, что событие появится ровно раз, выражается формулой

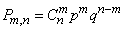, (4.1.1)

где .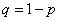

Формула (4.1.1) описывает, как распределяются вероятности между возможными значениями некоторойслучайной величины – числа появлений события при опытах.

В связи с тем, что вероятности по форме представляют собой члены разложения бинома ,распределение вероятностей вида (4.1.1) называют биномиальным распределением.