 |
Ряд распределения. Многоугольник распределения
|
|
|
|
В разделе курса, посвященном основным понятиям теории вероятностей, мы уже ввели в рассмотрение чрезвычайно важное понятие случайной величины. Здесь мы дадим дальнейшее развитие этого понятия и укажем способы, с помощью которых случайные величины могут быть описаны и характеризованы.
Как уже было сказано, случайной величиной называется величина, которая в результате опыта может принять то или иное значение, неизвестно заранее – какое именно. Мы условились также различать случайные величиныпрерывного (дискретного) и непрерывного типа. Возможные значения прерывных величин могут быть заранее перечислены. Возможные значения непрерывных величин не могут быть заранее перечислены и непрерывно заполняют некоторый промежуток.
Примеры прерывных случайных величин:
1) число появлений герба при трех бросаниях монеты (возможные значения 0, 1, 2, 3);
2) частота появления герба в том же опыте (возможные значения 
);
3) число отказавших элементов в приборе, состоящем из пяти элементов (возможнее значения 0, 1, 2, 3, 4, 5);
4) число попаданий в самолет, достаточное для вывода его из строя (возможные значения 1, 2, 3, …, n, …);
5) число самолетов, сбитых в воздушном бою (возможные значения 0, 1, 2, …, N, где 
– общее число самолетов, участвующих в бою).
Примеры непрерывных случайных величин:
1) абсцисса (ордината) точки попадания при выстреле;
2) расстояние от точки попадания до центра мишени;
3) ошибка измерителя высоты;
4) время безотказной работы радиолампы.
Условимся в дальнейшем случайные величины обозначать большими буквами, а их возможные значения – соответствующими малыми буквами. Например, 
– число попаданий при трех выстрелах; возможные значения: 
.
|
|
|
Рассмотрим прерывную случайную величину с возможными значениями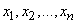 
. Каждое из этих значений возможно, но не достоверно, и величина Х может принять каждое из них с некоторой вероятностью. В результате опыта величина Х примет одно из этих значений, т.е. произойдет одно из полной группы несовместных событий:
(5.1.1)
Обозначим вероятности этих событий буквами p с соответствующими индексами:
Так как несовместные события (5.1.1) образуют полную группу, то
,
т.е. сумма вероятностей всех возможных значений случайной величины равна единице. Эта суммарная вероятностькаким-то образом распределена между отдельными значениями. Случайная величина будет полностью описана с вероятностной точки зрения, если мы зададим это распределение, т.е. в точности укажем, какой вероятностью обладает каждое из событий (5.1.1). Этим мы установим так называемый закон распределения случайной величины.
Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Про случайную величину мы будем говорить, что она подчинена данному закону распределения.
Установим форму, в которой может быть задан закон распределения прерывной случайной величины . Простейшей формой задания этого закона является таблица, в которой перечислены возможные значенияслучайной величины и соответствующие им вероятности:
Такую таблицу мы будем называть рядом распределения случайной величины .
Чтобы придать ряду распределения более наглядный вид, часто прибегают к его графическому изображению: по оси абсцисс откладываются возможные значения случайной величины, а по оси ординат – вероятности этих значений. Для наглядности полученные точки соединяются отрезками прямых. Такая фигура называется многоугольником распределения (рис. 5.1.1). Многоугольник распределения, так же как и ряд распределения, полностью характеризует случайную величину; он является одной из форм закона распределения.
|
|
|
Рис. 5.1.1.
Иногда удобной оказывается так называемая «механическая» интерпретация ряда распределения. Представим себе, что некоторая масса, равная единице, распределена по оси абсцисс так, что в 
отдельных точках 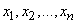сосредоточены соответственно массы 
. Тогда ряд распределения интерпретируется как система материальных точек с какими-то массами, расположенных на оси абсцисс.
Рассмотрим несколько примеров прерывных случайных величин с их законами распределения.
Пример 1. Производится один опыт, в котором может появиться или не появиться событие 
. Вероятность события равна 0,3. Рассматривается случайная величина – число появлений события в данном опыте (т.е. характеристическая случайная величина события , принимающая значение 1, если оно появится, и 0, если не появится). Построить ряд распределения и многоугольник распределения величины .
Решение. Величина имеет всего два значения: 0 и 1. Ряд распределения величины имеет вид:
Многоугольник распределения изображен на рис. 5.1.2.
Рис. 5.1.2.
Пример 2. Стрелок производит три выстрела по мишени. Вероятность попадания в мишень при каждом выстреле равна 0,4. За каждое попадание стрелку засчитывается 5 очков. Построить ряд распределения числа выбитых очков.
Решение. Обозначим число выбитых очков. Возможные значения величины : 
.
Вероятность этих значений находим по теореме о повторении опытов:
Ряд распределения величины имеет вид:
Многоугольник распределения изображен на рис. 5.1.3.
Рис. 5.1.3.
Пример 3. Вероятность появления события в одном опыте равна 
. Производится ряд независимых опытов, которые продолжаются до первого появления события , после чего опыты прекращаются. Случайная величина – число произведенных опытов. Построить ряд распределения величины .
Решение. Возможные значения величины : 1, 2, 3, … (теоретически они ничем не ограничены). Для того, чтобы величина приняла значение 1, необходимо, чтобы событие произошло в первом же опыте; вероятность этого равна . Для того, чтобы величина приняла значение 2, нужно, чтобы в первом опыте событие не появилось, а во втором – появилось; вероятность этого равна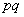 
, где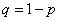 
, и т.д. Ряд распределения величины имеет вид:
|
|
|
Первые пять ординат многоугольника распределения для случая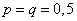 
показаны на рис. 5.1.4.
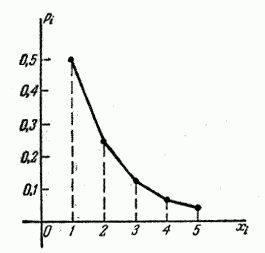
Рис. 5.1.4.
Пример 4. Стрелок ведет стрельбу по мишени до первого попадания, имея боезапас 4 патрона. Вероятностьпопадания при каждом выстреле равна 0,6. Построить ряд распределения боезапаса, оставшегося неизрасходованным.
Решение. Случайная величина – число неизрасходованных патронов – имеет четыре возможных значения: 0, 1, 2 и 3. Вероятности этих значений равны соответственно:
Ряд распределения величины имеет вид:
Многоугольник распределения показан на рис. 5.1.5.
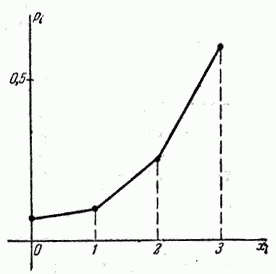
Рис. 5.1.5.
Пример 5. Техническое устройство может применяться в различных условиях и в зависимости от этого время от времени требует регулировки. При однократном применении устройства оно может случайным образом попасть в благоприятный или неблагоприятный режим. В благоприятном режиме устройство выдерживает три применения без регулировки; перед четвертым его приходится регулировать. В неблагоприятном режиме устройство приходится регулировать после первого же применения. Вероятность того, что устройство попадет в благоприятный режим, - 0,7, что в неблагоприятный, - 0,3. Рассматривается случайная величина – число применений устройства до регулировки. Построить её ряд распределения.
Решение. Случайная величина имеет три возможных значения: 1, 2 и 3. вероятность того, что 
, равна вероятности того, что при первом же применении устройство попадет в неблагоприятный режим, т.е. 
. Для того, чтобы величина приняла значение 2, нужно, чтобы при первом применении устройство попало в благоприятный режим, а при втором – в неблагоприятный; вероятность этого 
. Чтобы величина приняла значение 3, нужно, чтобы два первых раза устройство попало в благоприятный режим (после третьего раза его все равно придется регулировать). Вероятность этого равна 
.
Ряд распределения величины имеет вид:
Многоугольник распределения показан на рис. 5.1.6.
|
|
|
Рис. 5.1.6.
Функция распределения
В предыдущем n° мы ввели в рассмотрение ряд распределения как исчерпывающую характеристику (закон распределения) прерывной случайной величины. Однако эта характеристика не является универсальной; она существует только для прерывных случайных величин. Нетрудно убедиться, что для непрерывнойслучайной величины такой характеристики построить нельзя. Действительно, непрерывная случайная величинаимеет бесчисленное множество возможных значений, сплошь заполняющих некоторый промежуток (так называемое «счетное множество»). Составить таблицу, в которой были бы перечислены все возможные значения такой случайной величины, невозможно. Кроме того, как мы увидим в дальнейшем, каждое отдельное значение непрерывной случайной величины обычно не обладает никакой отличной от нуля вероятностью. Следовательно, для непрерывной случайной величины не существует ряда распределения в том смысле, в каком он существует для прерывной величины. Однако различные области возможных значений случайной величины все же не являются одинаково вероятными, и для непрерывной величины существует «распределение вероятностей», хотя и не в том смысле, как для прерывной.
Для количественной характеристики этого распределения вероятностей удобно воспользоваться невероятностью события 
, а вероятностью события 
, где 
– некоторая текущая переменная. Вероятностьэтого события, очевидно, зависит от , есть некоторая функция от . Эта функция называется функцией распределения случайной величины и обозначается 
:
. (5.2.1)
Функцию распределения иногда называют также интегральной функцией распределения или интегральным законом распределения.
Функция распределения – самая универсальная характеристика случайной величины. Она существует для всех случайных величин: как прерывных, так и непрерывных. Функция распределения полностью характеризуетслучайную величину с вероятностной точки зрения, т.е. является одной из форм закона распределения.
Сформулируем некоторые общие свойства функции распределения.
1. Функция распределения есть неубывающая функция своего аргумента, т.е. при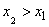 
.
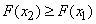2. На минус бесконечности функция распределения равна нулю: 
.
3. На плюс бесконечности функция распределения равна единице: 
.
Не давая строгого доказательства этих свойств, проиллюстрируем их с помощью наглядной геометрической интерпретации. Для этого будем рассматривать случайную величину как случайную точку на оси Ох (рис. 5.2.1), которая в результате опыта может занять то или иное положение. Тогда функция распределения естьвероятность того, что случайная точка в результате опыта попадет левее точки .
|
|
|
Рис. 5.2.1.
Будем увеличивать , т. е. перемещать точку вправо по оси абсцисс. Очевидно, при этом вероятность того, что случайная точка попадет левее , не может уменьшиться; следовательно, функция распределения с возрастанием убывать не может.
Чтобы убедиться в том, что , будем неограниченно перемещать точку влево по оси абсцисс. При этом попадание случайной точки левее в пределе становится невозможным событием; естественно полагать, чтовероятность этого события стремится к нулю, т.е. .
Аналогичным образом, неограниченно перемещая точку вправо, убеждаемся, что , так как событие становится в пределе достоверным.
График функции распределения в общем случае представляет собой график неубывающей функции (рис. 5.2.2), значения которой начинаются от 0 и доходят до 1, причем в отдельных точках функция может иметь скачки (разрывы).
Рис. 5.2.2.
Зная ряд распределения прерывной случайной величины, можно легко построить функцию распределения этой величины. Действительно,
,
где неравенство 
под знаком суммы указывает, что суммирование распространяется на все те значения 
, которые меньше .
Когда текущая переменная проходит через какое-нибудь из возможных значений прерывной величины , функция распределения меняется скачкообразно, причем величина скачка равна вероятности этого значения.
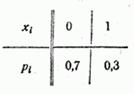
Пример 1. Производится один опыт, в котором может появиться или не появиться событие . Вероятность события равна 0,3. Случайная величина – число появлений события в опыте (характеристическая случайная величина события ). Построить её функцию распределения.
Решение. Ряд распределения величины имеет вид:
Построим функцию распределения величины :
1) при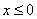 
;
2) при 
;
3) при 
.
График функции распределения представлен на рис. 5.2.3. В точках разрыва функция принимает значения, отмеченные на чертеже точками (функция непрерывна слева).
Рис. 5.2.3.
Пример 2. В условиях предыдущего примера производится 4 независимых опыта. Построить функцию распределения числа появлений события .
Решение. Обозначим – число появлений события в четырех опытах. Эта величина имеет ряд распределения
Построим функцию распределения случайной величины :
1) при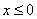 
;
2) при 
;
3) при 
;
4) при 
;
5) при 
;
6) при 
.
График функции распределения представлен на рис. 5.2.4.
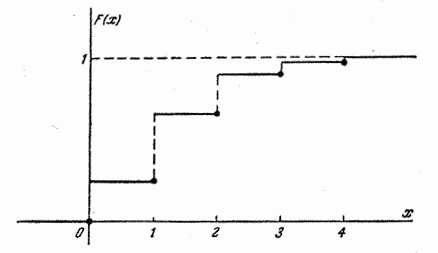
Рис. 5.2.4.
Функция распределения любой прерывной случайной величины всегда есть разрывная ступенчатая функция, скачки которой происходят в точках, соответствующих возможным случайным значениям величины, и равнывероятностям этих значений. Сумма всех скачков функции равна единице.
По мере увеличения числа возможных значений случайной величины и уменьшения интервалов между ними скачков становится больше, а сами скачки – меньше; ступенчатая кривая становится более плавной (рис. 5.2.5); случайна величина постепенно приближается к непрерывной величине, а её функция распределения – к непрерывной функции (рис. 5.2.6).
Рис. 5.2.5.
Рис. 5.2.6.
На практике обычно функция распределения непрерывной случайной величины представляет собой функцию, непрерывную во всех точках, как это показано на рис. 5.2.6. Однако можно построить примеры случайных величин, возможные значения которых непрерывно заполняют некоторый промежуток, но для которых функция распределения не везде является непрерывной, а в отдельных точках терпит разрыв (рис. 5.2.7).
Рис. 5.2.7.
Такие случайные величины называются смешанными. В качестве примера смешанной величины можно привести площадь разрушений, наносимых цели бомбой, радиус разрушительного действия которой равен R (рис. 5.2.8).
Рис. 5.2.8.
Значения этой случайной величины непрерывно заполняют промежуток от 0 до 
, осуществляющиеся при положениях бомбы типа I и II, обладают определенной конечной вероятностью, и этим значениям соответствуют скачки функции распределения, тогда как в промежуточных значениях (положение типа III) функция распределения непрерывна. Другой пример смешанной случайной величины – время T безотказной работы прибора, испытываемого в течение времени t. Функция распределения этой случайной величины непрерывна всюду, кроме точки t.
|
|
|
