 |
Линеаризация функции нескольких случайных аргументов
|
|
|
|
Имеется система 
случайных величин:
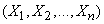
и заданы числовые характеристики системы: математические ожидания
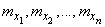
и корреляционная матрица
.
Случайная величина 
есть функция аргументов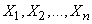 
:
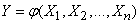, (11.3.1)
причем функция 
не линейна, но мало отличается от линейной в области практически возможных значений всех аргументов (короче, «почти линейная» функция). Требуется приближенно найти числовые характеристики величины - математическое ожидание 
и дисперсию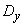 
.
Для решения задачи подвергнем линеаризации функцию
. (11.3.2)
В данном случае нет смысла пользоваться геометрической интерпретацией, так как за пределами трехмерного пространства она уже не обладает преимуществами наглядности. Однако качественная сторона вопроса остается совершенно той же, что и в предыдущем 
.
Рассмотрим функцию в достаточно малой окрестности точки 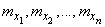. Так как функция в этой окрестности почти линейна, ее можно приближенно заменить линейной. Это равносильно тому, чтобы в разложении функции в ряд Тейлора около точки 
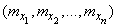сохранить только члены первого порядка, а все высшие отбросить:
.
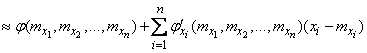Значит, и зависимость (11.3.1) между случайными величинами можно приближенно заменить линейной зависимостью:
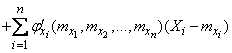. (11.3.3)
Введем для краткости обозначение:
.
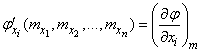Учитывая, что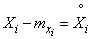 
, перепишем формулу (11.3.3) в виде:
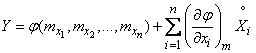(11.3.4)
К линейной функции (11.3.4) применим способы определения числовых характеристик линейных функций, выведенные в 10.2. Имея в виду, что центрированные аргументы 
имеютматематические ожидания, равные нулю, и ту же корреляционную матрицу 
, получим:
, (11.3.5)
(11.3.6)
Переходя в последней формуле от дисперсий к средним квадратическим отклонениям, получим:
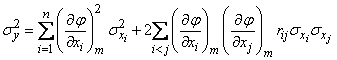, (11.3.7)
где 
- коэффициент корреляции величин 
.
|
|
|
Особенно простой вид принимает формула (11.3.7), когда величины 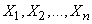не коррелированы, т. е. 
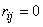при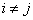 
.
В этом случае
.
Формулы типа (11.3.7) и (11.3.8) находят широкое применение в различных прикладных вопросах: при исследовании ошибок разного вида приборов и механизмов, а также при анализе точности стрельбы и бомбометания.
Пример 1. Относ бомбы 
(рис. 11.3.1) выражается приближенной аналитической формулой:
, (11.3.9)
где 
- скорость самолета (м/сек), 
- высота сбрасывания (м),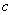 
- баллистический коэффициент.
Рис. 11.3.1
Высота определяется по высотомеру, скорость самолета - по указателю скорости, баллистический коэффициент 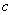принимается его номинальным значением 
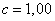. Высотомер показывает 4000 м, указатель скорости 150 м/сек. Показания высотомера характеризуются систематической ошибкой +50 м и средним квадратическим отклонением 
м; показания указателя скорости - систематической ошибкой - 2 м/сек и средним квадратическим отклонением 1 м/сек; разброс возможных значений баллистического коэффициента 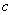, обусловленный неточностью изготовления бомбы, характеризуется средним квадратическим отклонением 
. Ошибки приборов независимы между собой.
Найти систематическую ошибку и среднее квадратическое отклонение точки падения бомбы вследствие неточности в определении параметров , и 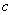. Определить, какой из этих факторов оказывает наибольшее влияние на разброс точки падения бомбы.
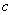Решение. Величины , и представляют собой некоррелированные случайные величины с числовыми характеристиками:
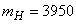м; м;
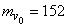м/сек; 
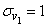м/сек;
; .
Так как диапазон возможных изменений случайных аргументов сравнительно невелик, для решения задачи можно применить метод линеаризации.
Подставляя в формулу (11.3.9) вместо величин , и 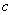их математические ожидания, найдемматематическое ожидание величины :
(м).
Для сравнения вычислим номинальное значение:
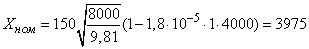(м).
Разность между математическим ожиданием и номинальным значением представляет собой систематическую ошибку точки падения:
|
|
|
(м).
Для определения дисперсии величины вычислим частные производные:
,
,
и подставим в эти выражения вместо каждого аргумента его математическое ожидание:
; 
; 
.
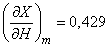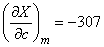По формуле (11.3.8) вычислим среднее квадратическое отклонение величины :
,
откуда
(м).
Сравнивая слагаемые, образующие 
, приходим к заключению, что наибольшее из них (697,0) обусловлено наличием ошибок в скорости ; следовательно, в данных условиях из рассмотренных случайных факторов, обусловливающих разброс точки падения бомбы, наиболее существенной является ошибка указателя скорости.
Пример 2. Абсцисса точки попадания (в метрах) при стрельбе по самолету выражается формулой
, (11.3.10)
где 
- ошибка наводки (м), 
- угловая скорость цели (рад/сек),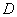 
- дальность стрельбы (м), 
- ошибка, связанная с баллистикой снаряда (м).
Величины 
представляют собой случайные величины с математическими ожиданиями:
; 
; 
; 
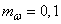и средними квадратнческими отклонениями:
; 
; 
; 
.
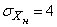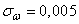Нормированная корреляционная матрица системы () (т. е. матрица, составленная изкоэффициентов корреляции) имеет вид:
.
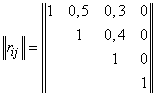Требуется найти математическое ожидание и среднее квадратическое отклонение величины .
Решение. Подставляя в формулу (11.3.10) математические ожидания аргументов, имеем:
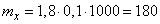(м).
Для определения среднего квадратического отклонения величины найдем частные производные:
; 
;
; 
.
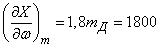Применяя формулу (11.3.7), имеем:
,
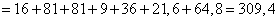откуда
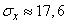(м).
|
|
|
