 |
Применения теорем о числовых характеристиках
|
|
|
|
В данном  мы продемонстрируем применение аппарата числовых характеристик к решению ряда задач. Некоторые из этих задач имеют самостоятельное теоретическое значение и найдут применение в дальнейшем. Другие задачи носят характер примеров и приводятся для иллюстрации выведенных общих формул на конкретном цифровом материале.
мы продемонстрируем применение аппарата числовых характеристик к решению ряда задач. Некоторые из этих задач имеют самостоятельное теоретическое значение и найдут применение в дальнейшем. Другие задачи носят характер примеров и приводятся для иллюстрации выведенных общих формул на конкретном цифровом материале.
Задача 1. Коэффициент корреляции линейно зависимых случайных величин.
Доказать, что если случайные величины  и
и  связаны линейной функциональной зависимостью
связаны линейной функциональной зависимостью
 ,
,
то их коэффициент корреляции равен  или
или  , смотря по знаку коэффициента
, смотря по знаку коэффициента  .
.
Решение. Имеем:

 ,
,
где  - дисперсия величины
- дисперсия величины  .
.
Для коэффициента корреляции имеем выражение:
 . (10.3.1)
. (10.3.1)
Для определения  найдем дисперсию величины
найдем дисперсию величины  :
:
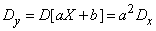 ,
,
 .
.
Подставляя в формулу (10.3.1), имеем:
 .
.
Величина  равна
равна  , когда
, когда  положительно, и
положительно, и  , когда
, когда  отрицательно, что и требовалось доказать.
отрицательно, что и требовалось доказать.
Задача 2. Границы коэффициента корреляции.
Доказать, что для любых случайных величин
 .
.
Решение. Рассмотрим случайную величину:
 ,
,
где  - средние квадратические отклонения величин
- средние квадратические отклонения величин 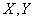 . Определим дисперсию величины
. Определим дисперсию величины  . По формуле (10.2.13) имеем:
. По формуле (10.2.13) имеем:
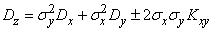 ,
,
или
 .
.
Так как дисперсия любой случайной величины не может быть отрицательна, то
 ,
,
или
 ,
,
откуда
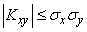 ,
,
а следовательно,
 ,
,
что и требовалось доказать.
Задача 3. Проектирование случайной точки на плоскости на произвольную прямую.
Дана случайная точка на плоскости с координатами 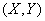 (рис. 10.3.1). Спроектируем эту точку на ось
(рис. 10.3.1). Спроектируем эту точку на ось  , проведенную через начало координат под углом
, проведенную через начало координат под углом  к оси
к оси  . Проекция точки
. Проекция точки 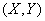 на ось
на ось  также есть случайная точка; ее расстояние
также есть случайная точка; ее расстояние  от начала координат есть случайная величина. Требуется найтиматематическое ожидание и дисперсию величины
от начала координат есть случайная величина. Требуется найтиматематическое ожидание и дисперсию величины  .
.

Рис.10.3.1
|
|
|
Решение. Имеем:
 .
.
Так как  есть линейная функция аргументов
есть линейная функция аргументов  и
и  , то
, то
 ;
;
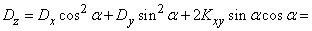
 ,
,
где  - дисперсии и корреляционный момент величин
- дисперсии и корреляционный момент величин 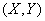 .
.
Переходя к средним квадратическим отклонениям, получим:
 . (10.3.2)
. (10.3.2)
В случае некоррелированных случайных величин (при  )
)
 . (10.3.3)
. (10.3.3)
Задача 4. Математическое ожидание числа появлений события при нескольких опытах.
Производится  опытов, в каждом из которых может появиться или не появиться событие
опытов, в каждом из которых может появиться или не появиться событие  . Вероятностьпоявления события
. Вероятностьпоявления события  в
в  -м опыте равна
-м опыте равна  . Найти математическое ожидание числа появлений события.
. Найти математическое ожидание числа появлений события.
Решение. Рассмотрим прерывную случайную величину  - число появлений события во всей серии опытов. Очевидно,
- число появлений события во всей серии опытов. Очевидно,
 ,
,
где 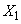 - число появлений события в первом опыте,
- число появлений события в первом опыте,
 - число появлений события во втором опыте,
- число появлений события во втором опыте,
………………………………………………….
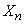 - число появлений события в
- число появлений события в  -м опыте,
-м опыте,
или, короче,
 ,
,
где 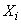 - число появлений события в
- число появлений события в  -м опыте.
-м опыте.
Каждая из величин 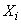 есть прерывная случайная величина с двумя возможными значениями:
есть прерывная случайная величина с двумя возможными значениями: 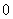 и
и  .Ряд распределения величины
.Ряд распределения величины 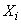 имеет вид:
имеет вид:
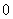
| 
|

| 
|
(10.3.4)
где  - вероятность непоявления события
- вероятность непоявления события  в
в  -м опыте.
-м опыте.
По теореме сложения математических ожиданий
 , (10.3.5)
, (10.3.5)
где  - математическое ожидание величины
- математическое ожидание величины 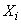 .
.
Вычислим математическое ожидание величины 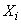 . По определению математического ожидания
. По определению математического ожидания
 .
.
Подставляя это выражение в формулу (10.3.5), имеем
 , (10.3.6)
, (10.3.6)
т. е. математическое ожидание числа появлений события при нескольких опытах равно сумме вероятностейсобытия в отдельных опытах.
В частности, когда условия опытов одинаковы и
 ,
,
формула (10.3.5) принимает вид
 . (10.3.7)
. (10.3.7)
Так как теорема сложения математических ожиданий применима к любым случайным величинам - как зависимым, так и независимым, формулы (10.3.6) и (10.3.7) применимы к любым опытам - зависимым и независимым.
Выведенная теорема часто применяется в теории стрельбы, когда требуется найти среднее число попаданий при нескольких выстрелах - зависимых или независимых. Математическое ожидание числа попаданий при нескольких выстрелах равно сумме вероятностей попадания при отдельных выстрелах.
|
|
|
Задача 5. Дисперсия числа появлений события при нескольких независимых опытах.
Производится  независимых опытов, в каждом из которых может появиться событие
независимых опытов, в каждом из которых может появиться событие  , причем вероятностьпоявления события
, причем вероятностьпоявления события  в
в  -м опыте равна
-м опыте равна  . Найти дисперсию и среднее квадратическое отклонение числа появлений события
. Найти дисперсию и среднее квадратическое отклонение числа появлений события  .
.
Решение. Рассмотрим случайную величину  - число появлений события
- число появлений события  . Так же как в предыдущей задаче, представим величину
. Так же как в предыдущей задаче, представим величину  в виде суммы:
в виде суммы:
 ,
,
где 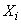 - число появлений события в
- число появлений события в  -м опыте.
-м опыте.
В силу независимости опытов случайные величины 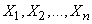 независимы и к ним применима теорема сложения дисперсий:
независимы и к ним применима теорема сложения дисперсий:
 .
.
Найдем дисперсию случайной величины 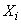 . Из ряда распределения (10.3.4) имеем:
. Из ряда распределения (10.3.4) имеем:
 ,
,
откуда
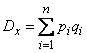 , (10.3.8)
, (10.3.8)
т. е. дисперсия числа появлений события при нескольких независимых опытах равна сумме вероятностей появления и непоявления события в каждом опыте.
Из формулы (10.3.8) находим среднее квадратическое отклонение числа появлений события  :
:
 . (10.3.9)
. (10.3.9)
При неизменных условиях опытов, когда  , формулы (10.3.8) и (10.3.9) упрощаются и принимают вид:
, формулы (10.3.8) и (10.3.9) упрощаются и принимают вид:
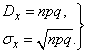 (10.3.10)
(10.3.10)
Задача 6. Дисперсия числа появлений события при зависимых опытах.
Производится  зависимых опытов, в каждом из которых может появиться событие
зависимых опытов, в каждом из которых может появиться событие  , причемвероятность события
, причемвероятность события  в
в  -м опыте равна
-м опыте равна 
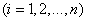 . Определить дисперсию числа появлений события.
. Определить дисперсию числа появлений события.
Решение. Для того чтобы решить задачу, снова представим число появлений события  в виде суммы:
в виде суммы:
 , (10.3.11)
, (10.3.11)
где

Так как опыты зависимы, то нам недостаточно задать вероятности

того, что событие  произойдет в первом, втором, третьем и т. д. опытах. Нужно еще задать характеристики зависимости опытов. Оказывается, для решения нашей задачи достаточно задать вероятности
произойдет в первом, втором, третьем и т. д. опытах. Нужно еще задать характеристики зависимости опытов. Оказывается, для решения нашей задачи достаточно задать вероятности  совместного появления события
совместного появления события  как в
как в  -м, так и в
-м, так и в  -м опыте:
-м опыте:  . Предположим, что эти вероятностизаданы. Применим к выражению (10.3.11) теорему о дисперсии суммы (формулу (10.2.10)):
. Предположим, что эти вероятностизаданы. Применим к выражению (10.3.11) теорему о дисперсии суммы (формулу (10.2.10)):
 , (10.3.12)
, (10.3.12)
где  - корреляционный момент величин
- корреляционный момент величин  :
:
 .
.
По формуле (10.2.19)
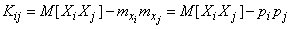 . (10.3.13)
. (10.3.13)
Рассмотрим случайную величину  . Очевидно она равна нулю, если хотя бы одна из величин
. Очевидно она равна нулю, если хотя бы одна из величин  равна нулю, т. е. хотя бы в одном из опытов (
равна нулю, т. е. хотя бы в одном из опытов ( -м или
-м или  -м) событие
-м) событие  не появилось. Для того чтобы величина
не появилось. Для того чтобы величина  была равна единице, требуется, чтобы в обоих опытах (
была равна единице, требуется, чтобы в обоих опытах ( -м и
-м и  -м) событие
-м) событие  появилось. Вероятность этого равна
появилось. Вероятность этого равна  . Следовательно,
. Следовательно,
|
|
|
 ,
,
и
 .
.
Подставляя это выражение в формулу (10.3.12), получим:
 . (10.3.14)
. (10.3.14)
Формула (10.3.14) и выражает дисперсию числа появлений события при зависимых опытах. Проанализируем структуру этой формулы. Первый член в правой части формулы представляет собой дисперсию числа появлений события при независимых опытах, а второй дает «поправку на зависимость». Если вероятность  равна
равна  , то эта поправка равна нулю. Если вероятность
, то эта поправка равна нулю. Если вероятность  больше, чем
больше, чем  , это значит, что условная вероятность появления события
, это значит, что условная вероятность появления события  в
в  -м опыте при условии, что в
-м опыте при условии, что в  -м опыте оно появилось, больше, чем простая (безусловная)вероятность появления события в
-м опыте оно появилось, больше, чем простая (безусловная)вероятность появления события в  -м опыте
-м опыте  (между появлениями события в
(между появлениями события в  -м и
-м и  -м опытах имеется положительная корреляция). Если это так для любой пары опытов, то поправочный член в формуле (10.3.14) положителен и дисперсия числа появлений события при зависимых опытах больше, чем при независимых.
-м опытах имеется положительная корреляция). Если это так для любой пары опытов, то поправочный член в формуле (10.3.14) положителен и дисперсия числа появлений события при зависимых опытах больше, чем при независимых.
Если вероятность  меньше, чем
меньше, чем  (между появлениями события в
(между появлениями события в  -м и
-м и  -м опытах существует отрицательная корреляция), то соответствующее слагаемое отрицательно. Если это так для любой пары опытов, тодисперсия числа появлений события при зависимых опытах меньше, чем при независимых.
-м опытах существует отрицательная корреляция), то соответствующее слагаемое отрицательно. Если это так для любой пары опытов, тодисперсия числа появлений события при зависимых опытах меньше, чем при независимых.
Рассмотрим частный случай, когда  ,
, 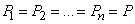 , т. е. условия всех опытов одинаковы. Формула (10.3.14) принимает вид:
, т. е. условия всех опытов одинаковы. Формула (10.3.14) принимает вид:
 , (10.3.15)
, (10.3.15)
где  - вероятность появления события
- вероятность появления события  сразу в паре опытов (все равно каких).
сразу в паре опытов (все равно каких).
В этом частном случае особый интерес представляют два подслучая:
1. Появление события  в любом из опытов влечет за собой с достоверностью его появление в каждом из остальных. Тогда
в любом из опытов влечет за собой с достоверностью его появление в каждом из остальных. Тогда  , и формула (10.3.15) принимает вид:
, и формула (10.3.15) принимает вид:
 .
.
2. Появление события  в любом из опытов исключает его появление в каждом из остальных. Тогда
в любом из опытов исключает его появление в каждом из остальных. Тогда  , и формула (10.3.15) принимает вид:
, и формула (10.3.15) принимает вид:
 .
.
Задача 7. Математическое ожидание числа объектов, приведенных в заданное состояние.
На практике часто встречается следующая задача. Имеется некоторая группа, состоящая из  объектов, по которым осуществляется какое-то воздействие. Каждый из объектов в результате воздействия может быть приведен в определенное состояние
объектов, по которым осуществляется какое-то воздействие. Каждый из объектов в результате воздействия может быть приведен в определенное состояние 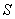 (например, поражен, исправлен, обнаружен, обезврежен и т. п.). Вероятность того, что
(например, поражен, исправлен, обнаружен, обезврежен и т. п.). Вероятность того, что  -й объект будет приведен в состояние
-й объект будет приведен в состояние 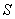 , равна
, равна  . Найти математическое ожидание числа объектов, которые в результате воздействия по группе будут приведены в состояние
. Найти математическое ожидание числа объектов, которые в результате воздействия по группе будут приведены в состояние 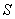 .
.
|
|
|
Решение. Свяжем с каждым из объектов случайную величину 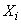 , которая принимает значения
, которая принимает значения 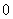 или
или  :
:

Случайная величина  - число объектов, приведенных в состояние
- число объектов, приведенных в состояние 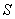 , - может быть представлена в виде суммы:
, - может быть представлена в виде суммы:
 .
.
Отсюда, пользуясь теоремой сложения математических ожиданий, получим:
 .
.
Математическое ожидание каждой из случайных величин 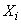 известно:
известно:
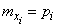 .
.
Следовательно,
 , (10.3.16)
, (10.3.16)
т. е. математическое ожидание числа объектов, приведенных в состояние 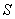 , равно сумме вероятностей перехода в это состояние для каждого из объектов.
, равно сумме вероятностей перехода в это состояние для каждого из объектов.
Особо подчеркнем, что для справедливости доказанной формулы вовсе не нужно, чтобы объекты переходили в состояние 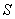 независимо друг от друга. Формула справедлива для любого вида воздействия.
независимо друг от друга. Формула справедлива для любого вида воздействия.
Задача 8. Дисперсия числа объектов, приведенных в заданное состояние.
Если в условиях предыдущей задачи переход каждого из объектов состояние 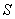 происходит независимо от всех других, то, применяя теорему сложения дисперсий к величине
происходит независимо от всех других, то, применяя теорему сложения дисперсий к величине
 ,
,
получим дисперсию числа объектов, приведенных в состояние 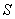 :
:
 ,
,  . (10.3.17)
. (10.3.17)
Если же воздействие по объектам производится так, что переходы в состояние 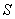 для отдельных объектов зависимы, то дисперсия числа объектов, переведенных в состояние
для отдельных объектов зависимы, то дисперсия числа объектов, переведенных в состояние 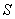 , выразится формулой (см. задачу 6)
, выразится формулой (см. задачу 6)
 , (10.3.18)
, (10.3.18)
где  - вероятность того, что в результате воздействия
- вероятность того, что в результате воздействия  -й и
-й и  -й объекты вместе перейдут в состояние
-й объекты вместе перейдут в состояние 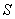 .
.
Задача 9. Математическое ожидание числа опытов до  -го появления события.
-го появления события.
Производится ряд независимых опытов, в каждом из которых может с вероятностью  появиться событие
появиться событие  . Опыты проводятся до тех пор, пока событие
. Опыты проводятся до тех пор, пока событие  не появится
не появится  раз, после чего опыты прекращаются. Определитьматематическое ожидание, дисперсию и с. к. о. числа опытов
раз, после чего опыты прекращаются. Определитьматематическое ожидание, дисперсию и с. к. о. числа опытов  , которое будет произведено.
, которое будет произведено.
Решение. В примере 3  5.7 были определены математическое ожидание и дисперсия числа опытов до первого появления события
5.7 были определены математическое ожидание и дисперсия числа опытов до первого появления события  :
:
 ,
,  ,
,
где  - вероятность появления события в одном опыте,
- вероятность появления события в одном опыте, 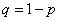 - вероятность непоявления.
- вероятность непоявления.
Рассмотрим случайную величину  - число опытов до
- число опытов до  -го появления события
-го появления события  . Ее можно представить в виде суммы:
. Ее можно представить в виде суммы:
 ,
,
где 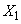 - число опытов до первого появления события
- число опытов до первого появления события  ,
,
 - число опытов от первого до второго появления события
- число опытов от первого до второго появления события  (считая второе),
(считая второе),
………………………………………………………………………………………
 - число опытов от
- число опытов от 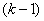 -го до
-го до  -го появления события
-го появления события  (считая
(считая  -е).
-е).
|
|
|
Очевидно, величины 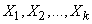 независимы; каждая из них распределена по тому же закону, что и первая из них (число опытов до первого появления события) и имеет числовые характеристики
независимы; каждая из них распределена по тому же закону, что и первая из них (число опытов до первого появления события) и имеет числовые характеристики
 ,
,  .
.
Применяя теоремы сложения математических ожиданий и дисперсий, получим:
 (10.3.19)
(10.3.19)
Задача 10. Средний расход средств до достижения заданного результата.
В предыдущей задаче был рассмотрен случай, когда предпринимается ряд опытов с целью получения вполне определенного результата -  появлений события
появлений события  , которое в каждом опыте имеет одну и ту же вероятность. Эта задача является частным случаем другой, когда производится ряд опытов с целью достижения любого результата
, которое в каждом опыте имеет одну и ту же вероятность. Эта задача является частным случаем другой, когда производится ряд опытов с целью достижения любого результата  , вероятность которого с увеличением числа опытов
, вероятность которого с увеличением числа опытов  возрастает по любому закону
возрастает по любому закону  . Предположим, что на каждый опыт расходуется определенное количество средств
. Предположим, что на каждый опыт расходуется определенное количество средств  . Требуется найти математическое ожидание количества средств, которое будет израсходовано.
. Требуется найти математическое ожидание количества средств, которое будет израсходовано.
Решение. Для того чтобы решить задачу, сначала предположим, что число производимых опытов ничем не ограничено, и что они продолжаются и после достижения результата  . Тогда некоторые из этих опытов будут излишними. Условимся называть опыт «необходимым», если он производится при еще не достигнутом результате
. Тогда некоторые из этих опытов будут излишними. Условимся называть опыт «необходимым», если он производится при еще не достигнутом результате  , и «излишним», если он производится при уже достигнутом результате
, и «излишним», если он производится при уже достигнутом результате  .
.
Свяжем с каждым ( -м) опытом случайную величину
-м) опытом случайную величину 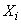 , которая равна нулю или единице в зависимости от того, «необходимым» или «излишним» оказался этот опыт. Положим
, которая равна нулю или единице в зависимости от того, «необходимым» или «излишним» оказался этот опыт. Положим

Рассмотрим случайную величину  - число опытов, которое придется произвести для получения результата
- число опытов, которое придется произвести для получения результата  . Очевидно, ее можно представить в виде суммы:
. Очевидно, ее можно представить в виде суммы:
 (10.3.20)
(10.3.20)
Из величин в правой части (10.3.20) первая  является неслучайной и всегда равна единице (первый опыт всегда «необходим»). Каждая из остальных - случайная величина с возможными значениями
является неслучайной и всегда равна единице (первый опыт всегда «необходим»). Каждая из остальных - случайная величина с возможными значениями 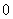 и
и  . Построимряд распределения случайной величины
. Построимряд распределения случайной величины 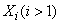 . Он имеет вид:
. Он имеет вид:
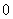
| 
|

| 
|
(10.3.21)
где  - вероятность достижения результата
- вероятность достижения результата  после
после  опытов.
опытов.
Действительно, если результат  уже был достигнут при предыдущих
уже был достигнут при предыдущих  опытах, то
опытах, то  (опыт излишен), если не достигнут, то
(опыт излишен), если не достигнут, то  (опыт необходим).
(опыт необходим).
Найдем математическое ожидание величины 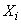 . Из ряда распределения (10.3.21) имеем:
. Из ряда распределения (10.3.21) имеем:
 .
.
Нетрудно убедиться, что та же формула будет справедлива и при  , так как
, так как  .
.
Применим к выражению (10.3.20) теорему сложения математических ожиданий. Получим:

или, обозначая  ,
,
 . (10.3.22)
. (10.3.22)
Каждый опыт требует затраты средств  . Умножая полученную величину
. Умножая полученную величину  на
на  , определим среднюю затрату средств на достижение результата
, определим среднюю затрату средств на достижение результата  :
:
 . (10.3.23)
. (10.3.23)
Данная формула выведена в предположении, что стоимость каждого опыта одна и та же. Если это не так, то можно применить другой прием - представить суммарную затрату средств  как сумму затрат на выполнение отдельных опытов, которая принимает два значения:
как сумму затрат на выполнение отдельных опытов, которая принимает два значения:  , если
, если  -й опыт «необходим», и нуль, если он «излишен». Средний расход средств
-й опыт «необходим», и нуль, если он «излишен». Средний расход средств  представится в виде:
представится в виде:
 . (10.3.24)
. (10.3.24)
Задача 11. Математическое ожидание суммы случайного числа случайных слагаемых.
В ряде практических приложений теории вероятностей приходится встречаться с суммами случайных величин, в которых число слагаемых заранее неизвестно, случайно.
Поставим следующую задачу. Случайная величина  представляет собой сумму
представляет собой сумму  случайных величин:
случайных величин:
 , (10.3.25)
, (10.3.25)
причем  - также случайная величина. Допустим, что нам известны математические ожидания
- также случайная величина. Допустим, что нам известны математические ожидания  всех слагаемых:
всех слагаемых:

и что величина  не зависит ни от одной из величин
не зависит ни от одной из величин 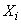 .
.
Требуется найти математическое ожидание величины  .
.
Решение. Число слагаемых в сумме есть дискретная случайная величина. Предположим, что нам известен ее ряд распределения:

| 
| 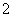
| 
| 
| 
|
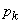
| 
| 
| 
| 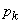
| 
|
где 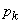 - вероятность того, что величина
- вероятность того, что величина  приняла значение
приняла значение  . Зафиксируем значение
. Зафиксируем значение  и найдем при этом условии математическое ожидание величины
и найдем при этом условии математическое ожидание величины  (условное математическое ожидание):
(условное математическое ожидание):
 . (10.3.26)
. (10.3.26)
Теперь применим формулу полного математического ожидания, для чего умножим каждое условное математическое ожидание на вероятность соответствующей гипотезы 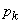 и сложим:
и сложим:
 . (10.3.27)
. (10.3.27)
Особый интерес представляет случай, когда все случайные величины  имеют одно и то же математическое ожидание:
имеют одно и то же математическое ожидание:
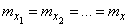 .
.
Тогда формула (10.3.26) принимает вид:

и
 . (10.3.28)
. (10.3.28)
Сумма в выражении (10.3.28) представляет собой не что иное, как математическое ожидание величины  :
:
 .
.
Отсюда
 , (10.3.29)
, (10.3.29)
т. е. математическое ожидание суммы случайного числа случайных слагаемых с одинаковыми средними значениями (если только число слагаемых не зависит от их значений) равно произведению среднего значениякаждого из слагаемых на среднее число слагаемых.
Снова отметим, что полученный результат справедлив как для независимых, так и для зависимых слагаемых  лишь бы число слагаемых
лишь бы число слагаемых  не зависело от самих слагаемых.
не зависело от самих слагаемых.
Ниже мы решим ряд конкретных примеров из разных областей практики, на которых продемонстрируем конкретное применение общих методов оперирования с числовыми характеристиками, вытекающих из доказанных теорем, и специфических приемов, связанных с решенными выше общими задачами.
Пример 1. Монета бросается 10 раз. Определить математическое ожидание и среднее квадратическое отклонение числа  выпавших гербов.
выпавших гербов.
Решение. По формулам (10.3.7) и (10.3.10) найдем:
 ;
; 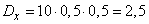 ;
;  .
.
Пример 2. Производится 5 независимых выстрелов по круглой мишени диаметром 20 см. Прицеливание - по центру мишени, систематическая ошибка отсутствует, рассеивание - круговое, среднее квадратическое отклонение  см. Найти математическое ожидание и с. к. о. числа попаданий.
см. Найти математическое ожидание и с. к. о. числа попаданий.
Решение. Вероятность попадания в мишень при одном выстреле вычислим по формуле (9.4.5):
 .
.
Пользуясь формулами (10.3.7) и (10.3.10), получим:
 ;
;  ;
; 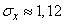 .
.
Пример 3. Производится отражение воздушного налета, в котором участвует 20 летательных аппаратов типа 1 и 30 летательных аппаратом типа 2. Летательные аппараты типа 1 атакуются истребительной авиацией. Число атак, приходящееся на каждый аппарат, подчинено закону Пуассона с параметром  . Каждой атакой истребителя летательный аппарат типа 1 поражается с вероятностью
. Каждой атакой истребителя летательный аппарат типа 1 поражается с вероятностью  . Летательные аппараты типа 2 атакуются зенитными управляемыми ракетами. Число ракет, направляемых на каждый аппарат, подчинено закону Пуассона с параметром
. Летательные аппараты типа 2 атакуются зенитными управляемыми ракетами. Число ракет, направляемых на каждый аппарат, подчинено закону Пуассона с параметром  , каждая ракета поражает летательный аппарат типа 2 с вероятностью
, каждая ракета поражает летательный аппарат типа 2 с вероятностью 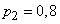 . Все аппараты, входящие в состав налета, атакуются и поражаются независимо друг от друга. Найти:
. Все аппараты, входящие в состав налета, атакуются и поражаются независимо друг от друга. Найти:
1) математическое ожидание, дисперсию и с. к. о. числа пораженных летательных аппаратов типа 1;
2) математическое ожидание, дисперсию и с. к. о. числа пораженных летательных аппаратов типа 2;
3) математическое ожидание, дисперсию и с. к. о. числа пораженных летательных аппаратов обоих типов.
Решение. Рассмотрим вместо «числа атак» на каждый аппарат типа 1 «число поражающих атак», тоже распределенное по закону Пуассона, но с другим параметром:
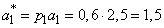 .
.
Вероятность поражения каждого из летательных аппаратов типа 1 будет равна вероятности того, что на него придется хотя бы одна поражающая атака:
 .
.
Вероятность поражения каждого из летательных аппаратов типа 2 найдем аналогично:
 .
.
Математическое ожидание числа пораженных аппаратов типа 1 будет:
 .
.
Дисперсия и с. к. о. этого числа:
 ,
, 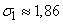 .
.
Математическое ожидание, дисперсия числа и с. к. о. пораженных аппаратов типа 2:
 ,
,  ,
,  .
.
Математическое ожидание, дисперсия и с. к. о. общего числа пораженных аппаратов обоих типов:
 ,
,  ,
, 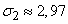 .
.
Пpимер 4. Случайные величины  и
и  представляют собой элементарные ошибки, возникающие на входе прибора. Они имеют математические ожидания
представляют собой элементарные ошибки, возникающие на входе прибора. Они имеют математические ожидания  и
и  , дисперсии
, дисперсии  и
и  ;коэффициент корреляции этих ошибок равен
;коэффициент корреляции этих ошибок равен  . Ошибка на выходе прибора связана с ошибками на входефункциональной зависимостью:
. Ошибка на выходе прибора связана с ошибками на входефункциональной зависимостью:
 .
.
Найти математическое ожидание ошибки на выходе прибора.
Решение.
 .
.
Пользуясь связью между начальными и центральными моментами и формулой (10.2.17), имеем:


