 |
Закон распределения суммы двух случайных величин. Композиция законов распределения
|
|
|
|
Воспользуемся изложенным выше общим методом для решения одной важной для практики частной задачи, а именно для нахождения закона распределения суммы двух случайных величин.
Имеется система двух случайных величин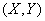 
с плотностью распределения 
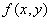. Рассмотрим сумму случайных величин 
и 
:
,
и 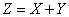найдем закон распределения величины 
. Для этого построим на плоскости 
линию, уравнение которой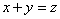 
(рис. 12.5.1). Это - прямая, отсекающая на осях отрезки, равные 
. Прямая 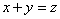делит плоскость на две части; правее и выше ее 
; левее и ниже 
. Область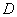 
в данном случае - левая нижняя часть плоскости , заштрихованная на рис. 12.5.1. Согласно формуле (12.4.2) имеем:
.
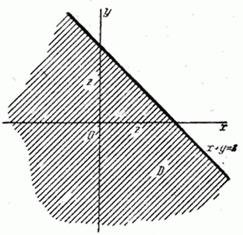
Рис. 12.5.1.
Дифференцируя это выражение по переменной , входящей в верхний предел внутреннего интеграла, получим:
. (12.5.1)
Это - общая формула для плотности распределения суммы двух случайных величин.
Из соображений симметричности задачи относительно и можно написать другой вариант той же формулы:
, (12.5.2)
который равносилен первому и может применяться вместо него.
Особое практическое значение имеет случай, когда складываемые случайные величины 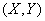независимы. Тогда говорят о композиции законов распределения.
Произвести композицию двух законов распределения это значит найти закон распределения суммы двух независимых случайных величин, подчиненных этим законам распределения.
Выведем формулу для композиции двух законов распределения. Имеются две независимые случайные величины и , подчиненные соответственно законам распределения 
и 
; требуется произвести композицию этих законов, т. е. найти плотность распределения величины
.
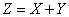Так как величины и независимы, то
,
и формулы (12.5.1) и (12.5.2) принимают вид:
|
|
|
, (12.5.3)
. (12.5.4)
Для обозначения композиции законов распределения часто применяют символическую запись:
,
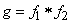где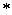 
- символ композиции.
Формулы (12.5.3) и (12.5.4) для композиции законов распределения удобны только тогда, когда законы распределения и 
(или, по крайней мере, один из них) заданы одной формулой на всем диапазоне значений аргумента (от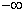 
до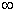 
). Если же оба закона заданы на различных участках различными уравнениями (например, два закона равномерной плотности), то удобнее пользоваться непосредственно общим методом, изложенным в 
12.4, т. е. вычислить функцию распределения 
величины 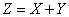и продифференцировать эту функцию.
Пример 1. Составить композицию нормального закона:
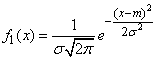
и закона равномерной плотности:
при 
.
Решение. Применим формулу композиции законов распределения в виде (12.5.4):
. (12.5.5)
Подынтегральная функция в выражении (12.5.5) есть не что иное, как нормальный закон с центром рассеивания 
и средним квадратическим отклонением 
, а интеграл в выражении (12.5.5) есть вероятность попаданияслучайной величины, подчиненной этому закону, на участок от 
до 
; следовательно,
.
Графики законов , и 
при 
, 
, 
, 
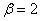приведены на рис. 12.5.2.
Рис. 12.5.2.
Пример 2. Составить композицию двух законов равномерной плотности, заданных на одном и том же участке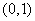 
:
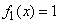при 
,
при 
.
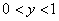Решение. Так как законы и заданы только на определенных участках осей 
и 
, для решения этой задачи удобнее воспользоваться не формулами (12.5.3) и (12.5.4), а общим методом, изложенным в 12.4, и найтифункцию распределения величины .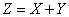
Рассмотрим случайную точку 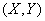на плоскости . Область ее возможных положений - квадрат 
со стороной, равной 1 (рис. 12.5.3).
Рис. 12.5.3.
Имеем
,
где область 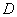- часть квадрата , лежащая левее и ниже прямой 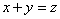. Очевидно,
,
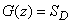где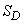 
- площадь области .
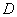Составим выражение для площади области 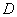при различных значениях , пользуясь рис. 12.5.3 и 12.5.4:
1) при 
;
2) при 
;
3) при 
;
4) при 
.
|
|
|
Рис. 12.5.4.
Дифференцируя эти выражения, получим
1) при 
;
2) при 
;
3) при 
;
4) при .
График закона распределения дан на рис. 12.5.5. Такой закон носит название «закона Симпсона» или «закона треугольника».
Рис. 12.5.5.
|
|
|
