 |
Система массового обслуживания с отказами. Уравнения Эрланга
|
|
|
|
Системы массового обслуживания делятся на два основных типа: а) системы с отказами, б) системы с ожиданием.
В системах с отказами заявка, поступившая в момент, когда все каналы обслуживания заняты, немедленно получает отказ, покидает систему и в дальнейшем процессе обслуживания не участвует.
В системах с ожиданием заявка, заставшая все каналы занятыми, не покидает систему, а становится в очередь и ожидает, пока не освободится какой-нибудь канал. В настоящем 
мы рассмотрим систему с отказами как наиболее простую.
Пусть имеется 
-канальная система массового обслуживания с отказами. Рассмотрим ее как физическую систему 
с конечным множеством состояний:
- свободны все каналы,
- занят ровно один канал,
……………
- занято ровно 
каналов,
……………
- заняты все каналов.
Схема возможных переходов дана на рис. 19.8.1.
Рис. 19.8.1.
Поставим задачу: определить вероятности состояний системы 
для любого момента времени 
. Задачу будем решать при следующих допущениях:
1) поток заявок - простейший, с плотностью
2) время обслуживания 
- показательное, с параметром 
. 
. (19.8.1)
Заметим, что параметр 
в формуле (19.8.1) полностью аналогичен параметру 
показательного закона распределения промежутка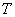 
между соседними событиями простейшего потока:
. (19.8.2)
Параметр имеет смысл «плотности потока заявок». Аналогично, величину можно истолковать как «плотность потока освобождений» занятого канала. Действительно, представим себе канал, непрерывно занятый (бесперебойно снабжаемый заявками); тогда, очевидно, в этом канале будет идти простейший поток освобождений с плотностью .
Так как оба потока - заявок и освобождений - простейшие, процесс, протекающий в системе, будет марковским.
|
|
|
Рассмотрим возможные состояния системы и их вероятности
. (19.8.3)
Очевидно, для любого момента времени
. (19.8.4)
Составим дифференциальные уравнения для всех вероятностей (19.8.3), начиная с 
. Зафиксируем момент времени и найдем вероятность 
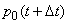того, что в момент 
система будет находиться в состоянии (все каналы свободны). Это может произойти двумя способами (рис. 19.8.2):
Рис. 19.8.2.
- в момент система находилась в состоянии , а за время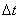 
не перешла из нее в (не пришло ни одной заявки),
- в момент система находилась в состоянии , а за время 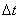канал освободился, и система перешла в состояние .
Возможностью «перескока» системы через состояние (например, из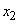 
в через ) за малый промежуток времени можно пренебречь, как величиной высшего порядка малости по сравнению с 
и 
.
По теореме сложения вероятностей имеем
. (19.8.5)
Найдем вероятность события по теореме умножения. Вероятность того, что в момент система была в состоянии , равна . Вероятность того, что за время 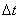не придет ни одной заявки, равна 
. С точностью до величин высшего порядка малости
. (19.8.6)
Следовательно,
.
Найдем . Вероятность того, что в момент система была в состоянии , равна 
. Вероятность того, что за время 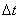канал освободится, равна 
с точностью до малых величин высшего порядка
.
Следовательно,
.
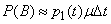Отсюда
.
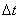Перенося в левую часть, деля на и переходя к пределу при 
, получим дифференциальное уравнениедля :
. (19.8.7)
Аналогичные дифференциальные уравнения могут быть составлены и для других вероятностей состояний.
Возьмем любое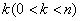 
и найдем вероятность 
того, что в момент система будет в состоянии (рис. 19.8.3).
Рис. 19.8.3.
Эта вероятность вычисляется как вероятность суммы уже не двух, а трех событий (по числу стрелок, направленных в состояние ):
- в момент система была в состоянии (занято каналов), а за время 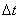не перешла из него ни в 
, ни в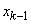 
(ни одна заявка не поступила, ни один канал не освободился);
|
|
|
- в момент система была в состоянии 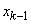(занято 
каналов), а за время 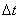перешла в (пришла одна заявка);
- в момент система была в состоянии (занято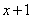 
каналов), а за время 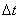один из каналов освободился.
Найдем . Вычислим сначала вероятность того, что за время 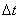не придет ни одна заявка и не освободится ни один из каналов:
.
Пренебрегая малыми величинами высших порядков, имеем
,
откуда
.
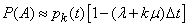Аналогично
,
и
.
Отсюда получаем дифференциальное уравнение для 
:
.
Составим уравнение для последней вероятности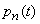 
(рис. 19.8.4).
Рис. 19.8.4.
Имеем
,
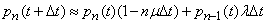где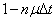 
- вероятность того, что за время 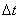не освободится ни один канал; 
- вероятность того, что за время 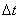придет одна заявка. Получаем дифференциальное уравнение для :
.
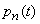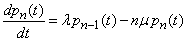Таким образом, получена система дифференциальных уравнений для вероятностей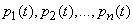 
:
(19.8.8)
Уравнения (19.8.8) называются уравнениями Эрланга. Интегрирование системы уравнений (19.8.8) при начальных условиях
; 
(в начальный момент все каналы свободны) дает зависимость для любого . Вероятности характеризуют среднюю загрузку системы и ее изменение с течением времени. В частности, 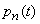естьвероятность того, что заявка, пришедшая в момент , застанет все каналы занятыми (получит отказ):
.
Величина 
называется относительной пропускной способностью системы. Для данного момента это есть отношение среднего числа обслуженных за единицу времени заявок к среднему числу поданных.
Система линейных дифференциальных уравнений (19.8.8) сравнительно легко может быть проинтегрирована при любом конкретном числе каналов .
Заметим, что при выводе уравнений (19.8.8) мы нигде не пользовались допущением о том, что величины и (плотности потока заявок и «потока освобождений») постоянны. Поэтому уравнения (19.8.8) остаются справедливыми и для зависящих от времени 
, 
, лишь бы потоки событий, переводящих систему из состоянии в состояние, оставались пуассоновскимн (без этого процесс не будет марковским).
|
|
|
