 |
Система массового обслуживания с ожиданием
|
|
|
|
Система массового обслуживания называется системой с ожиданием, если заявка, заставшая все каналы занятыми, становится в очередь и ждет, пока не освободится какой-нибудь канал.
Если время ожидания заявки в очереди ничем не ограничено, то система называется «чистой системой с ожиданием». Если оно ограничено какими-то условиями, то система называется «системой смешанного типа». Это промежуточный случай между чистой системой с отказами и чистой системой с ожиданием.
Для практики наибольший интерес представляют именно системы смешанного типа.
Ограничения, наложенные на ожидание, могут быть различного типа. Часто бывает, что ограничение накладывается на время ожидания заявки в очереди; считается, что оно ограничено сверху каким-то сроком  , который может быть как строго определенным, так и случайным. При этом ограничивается только срок ожидания в очереди, а начатое обслуживание доводится до конца, независимо от того, сколько времени продолжалось ожидание (например, клиент в парикмахерской, сев в кресло, обычно уже не уходит до конца обслуживания). В других задачах естественнее наложить ограничение не на время ожидания в очереди, а на общее время пребывания заявки в системе (например, воздушная цель может пробыть в зоне стрельбы лишь ограниченное время и покидает ее независимо от того, кончился обстрел или нет). Наконец, можно рассмотреть и такую смешанную систему (она ближе всего к типу торговых предприятий, торгующих предметами не первой необходимости), когда заявка становится в очередь только в том случае, если длина очереди не слишком велика. Здесь ограничение накладывается на число заявок в очереди.
, который может быть как строго определенным, так и случайным. При этом ограничивается только срок ожидания в очереди, а начатое обслуживание доводится до конца, независимо от того, сколько времени продолжалось ожидание (например, клиент в парикмахерской, сев в кресло, обычно уже не уходит до конца обслуживания). В других задачах естественнее наложить ограничение не на время ожидания в очереди, а на общее время пребывания заявки в системе (например, воздушная цель может пробыть в зоне стрельбы лишь ограниченное время и покидает ее независимо от того, кончился обстрел или нет). Наконец, можно рассмотреть и такую смешанную систему (она ближе всего к типу торговых предприятий, торгующих предметами не первой необходимости), когда заявка становится в очередь только в том случае, если длина очереди не слишком велика. Здесь ограничение накладывается на число заявок в очереди.
В системах с ожиданием существенную роль играет так называемая «дисциплина очереди». Ожидающие заявки могут вызываться на обслуживание как в порядке очереди (раньше прибывший раньше и обслуживается), так и в случайном, неорганизованном порядке. Существуют системы массового обслуживания «с преимуществами», где некоторые заявки обслуживаются предпочтительно перед другими («генералы и полковники вне очереди»).
|
|
|
Каждый тип системы с ожиданием имеет свои особенности и свою математическую теорию. Многие из них описаны, например, в книге В. В. Гнеденко «Лекции по теории массового обслуживания».
Здесь мы остановимся только на простейшем случае смешанной системы, являющемся естественным обобщением задачи Эрланга для системы с отказами. Для этого случая мы выведем дифференциальные уравнения, аналогичныеуравнениям Эрланга, и формулы для вероятностей состояний в установившемся режиме, аналогичныеформулам Эрланга.
Рассмотрим смешанную систему массового обслуживания  с
с  каналами при следующих условиях. На вход системы поступает простейший поток заявок с плотностью
каналами при следующих условиях. На вход системы поступает простейший поток заявок с плотностью  . Время обслуживания одной заявки
. Время обслуживания одной заявки  - показательное, с параметром
- показательное, с параметром  . Заявка, заставшая все каналы занятыми, становится в очередь и ожидает обслуживания; время ожидания ограничено некоторым сроком
. Заявка, заставшая все каналы занятыми, становится в очередь и ожидает обслуживания; время ожидания ограничено некоторым сроком  ; если до истечения этого срока заявка не будет принята к обслуживанию, то она покидает очередь и остается необслуженной. Срок ожидания
; если до истечения этого срока заявка не будет принята к обслуживанию, то она покидает очередь и остается необслуженной. Срок ожидания  будем считать случайным и распределенным по показательному закону
будем считать случайным и распределенным по показательному закону

 ,
,
где параметр  - величина, обратная среднему сроку ожидания:
- величина, обратная среднему сроку ожидания:
 ;
;  .
.
Параметр  полностью аналогичен параметрам
полностью аналогичен параметрам  и
и  потока заявок и «потока освобождений». Его можно интерпретировать, как плотность «потока уходов» заявки, стоящей в очереди. Действительно, представим себе заявку, которая только и делает, что становится в очередь и ждет в ней, пока не кончится срок ожидания
потока заявок и «потока освобождений». Его можно интерпретировать, как плотность «потока уходов» заявки, стоящей в очереди. Действительно, представим себе заявку, которая только и делает, что становится в очередь и ждет в ней, пока не кончится срок ожидания  , после чего уходит и сразу же снова становится в очередь. Тогда «поток уходов» такой заявки из очереди будет иметь плотность
, после чего уходит и сразу же снова становится в очередь. Тогда «поток уходов» такой заявки из очереди будет иметь плотность  .
.
|
|
|
Очевидно, при  система смешанного типа превращается в чистую систему с отказами; при
система смешанного типа превращается в чистую систему с отказами; при  она превращается в чистую систему с ожиданием.
она превращается в чистую систему с ожиданием.
Заметим, что при показательном законе распределения срока ожидания пропускная способность системы не зависит от того, обслуживаются ли заявки в порядке очереди или в случайном порядке: для каждой заявки закон распределения оставшегося времени ожидания не зависит от того, сколько времени заявка уже стояла в очереди.
Благодаря допущению о пуассоновском характере всех потоков событий, приводящих к изменениям состояний системы, процесс, протекающий в ней, будет марковским. Напишем уравнения для вероятностей состояний системы. Для этого, прежде всего, перечислим эти состояния. Будем их нумеровать не по числу занятых каналов, а по числу связанных с системой заявок. Заявку будем называть «связанной с системой», если она либо находится в состоянии обслуживания, либо ожидает очереди. Возможные состояния системы будут:
 - ни один канал не занят (очереди нет),
- ни один канал не занят (очереди нет),
 - занят ровно один канал (очереди нет),
- занят ровно один канал (очереди нет),
………
 - занято ровно
- занято ровно  каналов (очереди нет),
каналов (очереди нет),
………
 - заняты все
- заняты все  каналов (очереди нет),
каналов (очереди нет),
 - заняты все
- заняты все  каналов, одна заявка стоит в очереди,
каналов, одна заявка стоит в очереди,
………
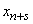 - заняты все
- заняты все  каналов,
каналов,  заявок стоят в очереди,
заявок стоят в очереди,
………
Число заявок  , стоящих в очереди, в наших условиях может быть сколь угодно большим. Таким образом, система
, стоящих в очереди, в наших условиях может быть сколь угодно большим. Таким образом, система  имеет бесконечное (хотя и счетное) множество состояний. Соответственно, число описывающих еедифференциальных уравнений тоже будет бесконечным.
имеет бесконечное (хотя и счетное) множество состояний. Соответственно, число описывающих еедифференциальных уравнений тоже будет бесконечным.
Очевидно, первые  дифференциальных уравнений ничем не будут отличаться от соответствующихуравнений Эрланга:
дифференциальных уравнений ничем не будут отличаться от соответствующихуравнений Эрланга:
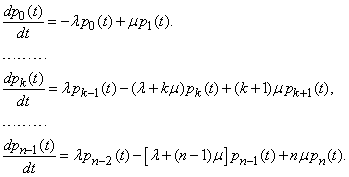
Отличие новых уравнений от уравнений Эрланга начнется при  . Действительно, в состояние
. Действительно, в состояние  система с отказами может перейти только из состояния
система с отказами может перейти только из состояния  ; что касается системы с ожиданием, то она может перейти в состояние
; что касается системы с ожиданием, то она может перейти в состояние  не только из
не только из  , но и из
, но и из  (все каналы заняты, одна заявка стоит в очереди).
(все каналы заняты, одна заявка стоит в очереди).
Составим дифференциальное уравнение для 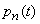 . Зафиксируем момент
. Зафиксируем момент  и найдем
и найдем  - вероятность того, что система в момент
- вероятность того, что система в момент  будет в состоянии
будет в состоянии  . Это может осуществиться тремя способами:
. Это может осуществиться тремя способами:
|
|
|
1) в момент  система уже была в состоянии
система уже была в состоянии  , а за время
, а за время 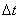 не вышла из него (не пришла ни одна заявка и ни один из каналов не освободился);
не вышла из него (не пришла ни одна заявка и ни один из каналов не освободился);
2) в момент  система была в состоянии
система была в состоянии  , а за время
, а за время 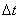 перешла в состояние
перешла в состояние  (пришла одна заявка);
(пришла одна заявка);
3) в момент  система была в состоянии
система была в состоянии  (все каналы заняты, одна заявка стоит в очереди), а за время
(все каналы заняты, одна заявка стоит в очереди), а за время 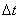 перешла в
перешла в  (либо освободился один канал и стоящая в очереди заявка заняла его, либо стоящая в очереди заявка ушла в связи с окончанием срока).
(либо освободился один канал и стоящая в очереди заявка заняла его, либо стоящая в очереди заявка ушла в связи с окончанием срока).
Имеем:
 ,
,
откуда
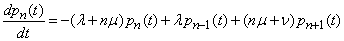 .
.
Вычислим теперь  при любом
при любом 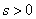 - вероятность того, что в момент
- вероятность того, что в момент  все
все  каналов будут заняты и ровно
каналов будут заняты и ровно  заявок будут стоять в очереди. Это событие снова может осуществиться тремя способами:
заявок будут стоять в очереди. Это событие снова может осуществиться тремя способами:
1) в момент  система уже была в состоянии
система уже была в состоянии 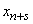 , а за время
, а за время 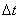 это состояние не изменилось (значит, ни одна заявка не пришла, ни один капал не освободился и ни одна из
это состояние не изменилось (значит, ни одна заявка не пришла, ни один капал не освободился и ни одна из  стоящих в очереди заявок не ушла);
стоящих в очереди заявок не ушла);
2) в момент  система была в состоянии
система была в состоянии  , а за время
, а за время 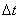 перешла в состояние
перешла в состояние 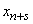 (т. е. пришла одна заявка);
(т. е. пришла одна заявка);
3) в момент  система была в состоянии
система была в состоянии  , а за время
, а за время 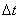 перешла в состояние
перешла в состояние 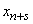 (для этого либо один из каналов должен освободиться, и тогда одна из
(для этого либо один из каналов должен освободиться, и тогда одна из  стоящих в очереди заявок займет его, либо одна из стоящих в очереди заявок должна уйти в связи с окончанием срока).
стоящих в очереди заявок займет его, либо одна из стоящих в очереди заявок должна уйти в связи с окончанием срока).
Следовательно:
 ,
,
откуда
 .
.
Таким образом, мы получили для вероятностей состояний систему бесконечного числадифференциальных уравнений:
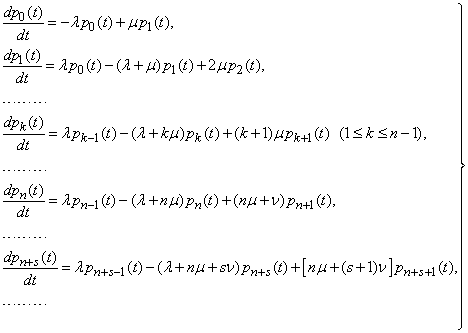 (19.10.1)
(19.10.1)
Уравнения (19.10.1) являются естественным обобщением уравнений Эрланга на случай системы смешанного типа с ограниченным временем ожидания. Параметры  в этих уравнениях могут быть как постоянными, так и переменными. При интегрировании системы (19.10.1) нужно учитывать, что хотя теоретически число возможных состояний системы бесконечно, но на практике вероятности
в этих уравнениях могут быть как постоянными, так и переменными. При интегрировании системы (19.10.1) нужно учитывать, что хотя теоретически число возможных состояний системы бесконечно, но на практике вероятности  при возрастании
при возрастании  становятся пренебрежимо малыми, и соответствующие уравнения могут быть отброшены.
становятся пренебрежимо малыми, и соответствующие уравнения могут быть отброшены.
Выведем формулы, аналогичные формулам Эрланга, для вероятностей состояний системы при установившемся режиме обслуживания (при  ). Из уравнений (19.10.1), полагая все
). Из уравнений (19.10.1), полагая все 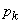
 постоянными, а всепроизводные - равными нулю, получим систему алгебраических уравнений:
постоянными, а всепроизводные - равными нулю, получим систему алгебраических уравнений:
|
|
|
 (19.10.2)
(19.10.2)
К ним нужно присоединить условие:
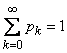 . (19.10.3)
. (19.10.3)
Найдем решение системы (19.10.2).
Для этого применим тот же прием, которым мы пользовались в случае системы с отказами: разрешим первое уравнение относительно  подставим во второе, и т. д. Для любого
подставим во второе, и т. д. Для любого  , как и в случае системы с отказами, получим:
, как и в случае системы с отказами, получим:
 . (19.10.4)
. (19.10.4)
Перейдем к уравнениям для 
 . Тем же способом получим:
. Тем же способом получим:
 ,
,
 ,
,
и вообще при любом 
 . (19.10.5)
. (19.10.5)
В обе формулы (19.10.4) и (19.10.5) в качестве сомножителя входит вероятность  . Определим ее из условия (19.10.3). Подставляя в него выражения (19.10.4) и (19.10.5) для
. Определим ее из условия (19.10.3). Подставляя в него выражения (19.10.4) и (19.10.5) для  и
и  , получим:
, получим:
 ,
,
откуда
 . (19.10.6)
. (19.10.6)
Преобразуем выражения (19.10.4), (19.10.5) и (19.10.6), вводя в них вместо плотностей  и
и  «приведенные» плотности:
«приведенные» плотности:
 (19.10.7)
(19.10.7)
Параметры  и
и  выражают соответственно среднее число заявок и среднее число уходов заявки, стоящей в очереди, приходящиеся на среднее время обслуживания одной заявки.
выражают соответственно среднее число заявок и среднее число уходов заявки, стоящей в очереди, приходящиеся на среднее время обслуживания одной заявки.
В новых обозначениях формулы (19.10.4), (19.10.5) и (19.10.6) примут вид:

 ; (19.10.8)
; (19.10.8)

 ; (19.10.9)
; (19.10.9)
 . (19.10.10)
. (19.10.10)
Подставляя (19.10.10) в (19.10.8) и (19.10.9), получим окончательные выражения для вероятностей состояний системы:

 ; (19.10.11)
; (19.10.11)

 . (19.10.12)
. (19.10.12)
Зная вероятности всех состояний системы, можно легко определить другие интересующие нас характеристики, в частности, вероятность  того, что заявка покинет систему необслуженной. Определим ее из следующих соображений: при установившемся режиме вероятность
того, что заявка покинет систему необслуженной. Определим ее из следующих соображений: при установившемся режиме вероятность  того, что заявка покинет систему необслуженной, есть не что иное, как отношение среднего числа заявок, уходящих из очереди в единицу времени, к среднему числу заявок, поступающих в единицу времени. Найдем среднее число заявок уходящих из очереди в единицу времени. Для этого сначала вычислим математическое ожидание
того, что заявка покинет систему необслуженной, есть не что иное, как отношение среднего числа заявок, уходящих из очереди в единицу времени, к среднему числу заявок, поступающих в единицу времени. Найдем среднее число заявок уходящих из очереди в единицу времени. Для этого сначала вычислим математическое ожидание  числа заявок, находящихся в очереди:
числа заявок, находящихся в очереди:
 . (19.10.13)
. (19.10.13)
Чтобы получить  , нужно
, нужно  умножить на среднюю «плотность уходов» одной заявки
умножить на среднюю «плотность уходов» одной заявки  и разделить на среднюю плотность заявок
и разделить на среднюю плотность заявок  , т. е. умножить на коэффициент
, т. е. умножить на коэффициент
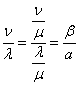 .
.
Получим:
 . (19.10.14)
. (19.10.14)
Относительная пропускная способность системы характеризуется вероятностью того, что заявка, попавшая в систему, будет обслужена:
 .
.
Очевидно, что пропускная способность системы с ожиданием, при тех же  и
и  , будет всегда выше, чем пропускная способность системы с отказами: в случае наличия ожидания необслуженными уходят не все заявки, заставшие
, будет всегда выше, чем пропускная способность системы с отказами: в случае наличия ожидания необслуженными уходят не все заявки, заставшие  каналов занятыми, а только некоторые. Пропускная способность увеличивается при увеличении среднего времени ожидания
каналов занятыми, а только некоторые. Пропускная способность увеличивается при увеличении среднего времени ожидания 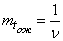 .
.
Непосредственное пользование формулами (19.10.11), (19.10.12) и (19.10.14) несколько затруднено тем, что в них входят бесконечные суммы. Однако члены этих сумм быстро убывают.
Посмотрим, во что превратятся формулы (19.10.11) и (19.10.12) при 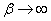 и
и  . Очевидно, что при
. Очевидно, что при 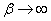 система с ожиданием должна превратиться в систему с отказами (заявка мгновенно уходит из очереди). Действительно, при
система с ожиданием должна превратиться в систему с отказами (заявка мгновенно уходит из очереди). Действительно, при 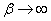 формулы (19.10.12) дадут нули, а формулы (19.10.11) превратятся в формулы Эрлангадля системы с отказами.
формулы (19.10.12) дадут нули, а формулы (19.10.11) превратятся в формулы Эрлангадля системы с отказами.
|
|
|
Рассмотрим другой крайний случай: чистую систему с ожиданием 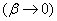 . В такой системе заявки вообще не уходят из очереди, и поэтому
. В такой системе заявки вообще не уходят из очереди, и поэтому  : каждая заявка рано или поздно дождется обслуживания. Зато в чистой системе с ожиданием не всегда имеется предельный стационарный режим при
: каждая заявка рано или поздно дождется обслуживания. Зато в чистой системе с ожиданием не всегда имеется предельный стационарный режим при  . Можно доказать, что такой режим существует только при
. Можно доказать, что такой режим существует только при  , т. е. когда среднее число заявок, приходящееся на время обслуживания одной заявки, не выходит за пределы возможностей
, т. е. когда среднее число заявок, приходящееся на время обслуживания одной заявки, не выходит за пределы возможностей  -канальной системы. Если же
-канальной системы. Если же  , число заявок, стоящих в очереди, будет с течением времени неограниченно возрастать.
, число заявок, стоящих в очереди, будет с течением времени неограниченно возрастать.
Предположим, что  , и найдем предельные вероятности
, и найдем предельные вероятности 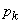
 для чистой системы с ожиданием. Для этого положим в формулах (19.9.10), (19.9.11) и (19.9.12)
для чистой системы с ожиданием. Для этого положим в формулах (19.9.10), (19.9.11) и (19.9.12)  . Получим:
. Получим:
 ,
,
или, суммируя прогрессию (что возможно только при  ),
),
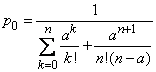 . (19.10.15)
. (19.10.15)
Отсюда, пользуясь формулами (19.10.8) и (19.10.9), найдем

 , (19.10.16)
, (19.10.16)
и аналогично для 
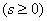
 . (19.10.17)
. (19.10.17)
Среднее число заявок, находящихся в очереди, определяется из формулы (19.10.13) при  :
:
 . (19.10.18)
. (19.10.18)
Пример 1. На вход трехканальной системы с неограниченным временем ожидания поступает простейший потокзаявок с плотностью 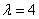 (заявки в час). Среднее время обслуживания одной заявки
(заявки в час). Среднее время обслуживания одной заявки  мин. Определить, существует ли установившийся режим обслуживания; если да, то найти вероятности
мин. Определить, существует ли установившийся режим обслуживания; если да, то найти вероятности 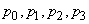 , вероятностьналичия очереди и среднюю длину очереди
, вероятностьналичия очереди и среднюю длину очереди  .
.
Решение. Имеем  ;
;  . Так как
. Так как  , установившийся режим существует. По формуле (19.10.16) находим
, установившийся режим существует. По формуле (19.10.16) находим
 ;
;  ;
;  ;
; 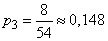 .
.
Вероятность наличия очереди:
 .
.
Средняя длина очереди по формуле (19.10.18) будет
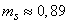 (заявки).
(заявки).
|
|
|


