 |
Система смешанного типа с ограничением по длине очереди
|
|
|
|
В предыдущем  мы рассмотрели систему массового обслуживания с ограничением по времени пребывания в очереди. Здесь мы рассмотрим систему смешанного типа с другим видом ограничения ожидания - по числу заявок, стоящих в очереди. Предположим, что заявка, заставшая все каналы занятыми, становится в очередь, только если в ней находится менее
мы рассмотрели систему массового обслуживания с ограничением по времени пребывания в очереди. Здесь мы рассмотрим систему смешанного типа с другим видом ограничения ожидания - по числу заявок, стоящих в очереди. Предположим, что заявка, заставшая все каналы занятыми, становится в очередь, только если в ней находится менее  заявок; если же число заявок в очереди равно
заявок; если же число заявок в очереди равно  (больше
(больше  оно быть не может), то последняя прибывшая заявка в очередь не становится и покидает систему необслуженной. Остальные допущения - о простейшем потоке заявок и о показательном распределении времени обслуживания - оставим прежними.
оно быть не может), то последняя прибывшая заявка в очередь не становится и покидает систему необслуженной. Остальные допущения - о простейшем потоке заявок и о показательном распределении времени обслуживания - оставим прежними.
Итак, имеется  -канальная система с ожиданием, в которой количество заявок, стоящих в очереди, ограничено числом
-канальная система с ожиданием, в которой количество заявок, стоящих в очереди, ограничено числом  . Составим дифференциальные уравнения для вероятностей состояний системы. Заметим, что в данном случае число состояний системы будет конечно, так как общее число заявок, связанных с системой, не может превышать
. Составим дифференциальные уравнения для вероятностей состояний системы. Заметим, что в данном случае число состояний системы будет конечно, так как общее число заявок, связанных с системой, не может превышать  (
( обслуживаемых и
обслуживаемых и  стоящих в очереди). Перечислим состояния системы:
стоящих в очереди). Перечислим состояния системы:
 - все каналы свободны, очереди нет,
- все каналы свободны, очереди нет,
 - занят один канал, очереди нет,
- занят один канал, очереди нет,
………
 - занято
- занято  каналов, очереди нет,
каналов, очереди нет,
………
 - занято
- занято 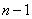 каналов, очереди нет,
каналов, очереди нет,
 - заняты все
- заняты все  каналов, очереди нет,
каналов, очереди нет,
 - заняты все
- заняты все  каналов, одна заявка стоит в очереди,
каналов, одна заявка стоит в очереди,
………
 - заняты все
- заняты все  каналов,
каналов,  заявок стоит в очереди.
заявок стоит в очереди.
Очевидно, первые  уравнений для вероятностей
уравнений для вероятностей  будут совпадать с уравнениями Эрланга (19.8.8). Выведем остальные уравнения. Имеем
будут совпадать с уравнениями Эрланга (19.8.8). Выведем остальные уравнения. Имеем
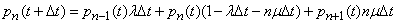 ,
,
откуда
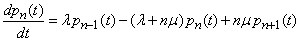 .
.
Далее выведем уравнение для 

 ,
,
откуда
 .
.
Последнее уравнение будет
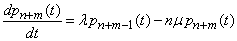 .
.
Таким образом, получена система  дифференциальных уравнений:
дифференциальных уравнений:
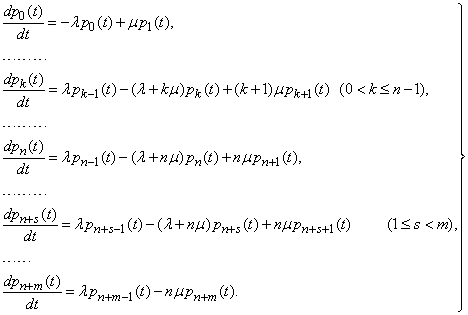 (19.11.1)
(19.11.1)
Рассмотрим предельный случай при  . Приравнивая все производные нулю, а все вероятности считая постоянными, получим систему алгебраических уравнений
. Приравнивая все производные нулю, а все вероятности считая постоянными, получим систему алгебраических уравнений
|
|
|
 (19.11.2)
(19.11.2)
и добавочное условие:
 . (19.11.3)
. (19.11.3)
Уравнения (19.11.2) могут быть решены так же, как мы решили аналогичные алгебраические уравнения в предыдущих 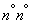 . Не останавливаясь на этом решении, приведем только окончательные формулы:
. Не останавливаясь на этом решении, приведем только окончательные формулы:

 , (19.11.4)
, (19.11.4)
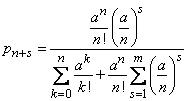
 . (19.11.5)
. (19.11.5)
Вероятность того, что заявка покинет систему необслуженной, равна вероятности 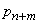 того, что в очереди уже стоят
того, что в очереди уже стоят  заявок.
заявок.
Нетрудно заметить, что формулы (19.11.4) и (19.11.5) получаются из формул (19.10.11), (19.10.12), если положить в них  и ограничить суммирование по
и ограничить суммирование по  верхней границей
верхней границей  .
.
Пример. На станцию текущего ремонта автомашин поступает простейший поток заявок с плотностью 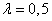 (машины в час). Имеется одно помещение для ремонта. Во дворе станции могут одновременно находиться, ожидая очереди, не более трех машин. Среднее время ремонта одной машины
(машины в час). Имеется одно помещение для ремонта. Во дворе станции могут одновременно находиться, ожидая очереди, не более трех машин. Среднее время ремонта одной машины  (часа). Определить: а) пропускную способность системы; б) среднее время простоя станции; в) определить, насколько изменятся эти характеристики, если оборудовать второе помещение для ремонта.
(часа). Определить: а) пропускную способность системы; б) среднее время простоя станции; в) определить, насколько изменятся эти характеристики, если оборудовать второе помещение для ремонта.
Решение. Имеем: 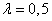 ,
,  ,
,  ,
,  .
.
а) По формуле (19.11.5), полагая 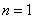 , находим вероятность того, что пришедшая заявка покинет систему необслуженной:
, находим вероятность того, что пришедшая заявка покинет систему необслуженной:
 .
.
Относительная пропускная способность системы  . Абсолютная пропускная способность:
. Абсолютная пропускная способность: 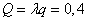 (машины в час).
(машины в час).
б) Средняя доля времени, которое система будет простаивать, найдем по формуле (19.11.4):  .
.
в) Полагая  , найдем:
, найдем:
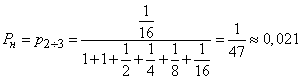 ,
,
 (т. е. удовлетворяться будет около 98% всех заявок).
(т. е. удовлетворяться будет около 98% всех заявок).
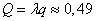 (машины в час).
(машины в час).
Относительное время простоя:  , т. е. оборудование будет простаивать полностью около 34% всего времени.
, т. е. оборудование будет простаивать полностью около 34% всего времени.
Приложения
Таблица 1 Значения нормальной функции распределения:
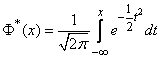

| 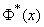
| 
| 
| 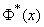
| 
| 
| 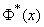
| 
|
| -0,00 | 0,5000 | -0,30 | 0,3821 | -0,60 | 0,2743 | |||
| -0,01 | -0,31 | -0,61 | ||||||
| -0,02 | -0,32 | -0,62 | ||||||
| -0,03 | -0,33 | -0,63 | ||||||
| -0,04 | -0,34 | -0,64 | ||||||
| -0,05 | -0,35 | -0,65 | ||||||
| -0,06 | -0,36 | -0,66 | ||||||
| -0,07 | -0,37 | -0,67 | ||||||
| -0,08 | -0,38 | -0,68 | ||||||
| -0,09 | -0,39 | -0,69 | ||||||
| -0,10 | 0,4602 | -0,40 | 0,3446 | -0,70 | 0,2420 | |||
| -0,11 | -0,41 | -0,71 | ||||||
| -0,12 | -0,42 | -0,72 | ||||||
| -0,13 | -0,43 | -0,73 | ||||||
| -0,14 | -0,44 | -0,74 | ||||||
| -0,15 | -0,45 | -0,75 | ||||||
| -0,16 | -0,46 | -0,76 | ||||||
| -0,17 | -0,47 | -0,77 | ||||||
| -0,18 | -0,48 | -0,78 | ||||||
| -0,19 | -0,49 | -0,79 | ||||||
| -0,20 | 0,4207 | -0,50 | 0,3085 | -0,80 | 0,2119 | |||
| -0,21 | -0,51 | -0,81 | ||||||
| -0,22 | -0,52 | -0,82 | ||||||
| -0,23 | -0,53 | -0,83 | ||||||
| -0,24 | -0,54 | -0,84 | ||||||
| -0,25 | -0,55 | -0,85 | ||||||
| -0,26 | -0,56 | -0,86 | ||||||
| -0,27 | -0,57 | -0,87 | ||||||
| -0,28 | -0,58 | -0,88 | ||||||
| -0,29 | -0,59 | -0,89 | ||||||

| 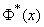
| 
| 
| 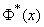
| 
| 
| 
| 
|
| -0,90 | 0,1841 | -1,30 | 0,0968 | -1,70 | 0,0446 | |||
| -0,91 | -1,31 | -1,71 | ||||||
| -0,92 | -1,32 | -1,72 | ||||||
| -0,93 | -1,33 | -1,73 | ||||||
| -0,94 | -1,34 | -1,74 | ||||||
| -0,95 | -1,35 | -1,75 | ||||||
| -0,96 | -1,36 | -1,76 | ||||||
| -0,97 | -1,37 | -1,77 | ||||||
| -0,98 | -1,38 | -1,78 | ||||||
| -0,99 | -1,39 | -1,79 | ||||||
| -1,00 | 0,1587 | -1,40 | 0,0808 | -1,80 | 0,0359 | |||
| -1,01 | -1,41 | -1,81 | ||||||
| -1,02 | -1,42 | -1,82 | ||||||
| -1,03 | -1,43 | -1,83 | ||||||
| -1,04 | -1,44 | -1,84 | ||||||
| -1,05 | -1,45 | -1,85 | ||||||
| -1,06 | -1,46 | -1,86 | ||||||
| -1,07 | -1,47 | -1,87 | ||||||
| -1,08 | -1,48 | -1,88 | ||||||
| -1,09 | -1,49 | -1,89 | ||||||
| -1,10 | 0,1357 | -1,50 | 0,0668 | -1,90 | 0,0288 | |||
| -1,11 | -1,51 | -1,91 | ||||||
| -1,12 | -1,52 | -1,92 | ||||||
| -1,13 | -1,53 | -1,93 | ||||||
| -1,14 | -1,54 | -1,94 | ||||||
| -1,15 | -1,55 | -1,95 | ||||||
| -1,16 | -1,56 | -1,96 | ||||||
| -1,17 | -1,57 | -1,97 | ||||||
| -1,18 | -1,58 | -1,98 | ||||||
| -1,19 | -1,59 | -1,99 | ||||||
| -1,20 | 0,1151 | -1,60 | 0,0548 | -2,00 | 0,0228 | |||
| -1,21 | -1,61 | -2,10 | ||||||
| -1,22 | -1,62 | -2,20 | ||||||
| -1,23 | -1,63 | -2,50 | ||||||
| -1,24 | -1,64 | -2,40 | ||||||
| -1,25 | -1,65 | -2,50 | ||||||
| -1,26 | -1,66 | -2,60 | ||||||
| -1,27 | -1,67 | -2,70 | ||||||
| -1,28 | -1,68 | -2,80 | ||||||
| -1,29 | -1,69 | -2,90 | ||||||

| 
| 
| 
| 
| 
| 
| 
| 
|
| -3,00 | 0,0014 | 0,30 | 0,6179 | 0,70 | 0,7580 | |||
| -3,10 | 0,31 | 0,71 | ||||||
| -3,20 | 0,32 | 0,72 | ||||||
| -3,30 | 0,33 | 0,73 | ||||||
| -3,40 | 0,34 | 0,74 | ||||||
| -3,50 | 0,35 | 0,75 | ||||||
| -3,60 | 0,36 | 0,76 | ||||||
| -3,70 | 0,37 | 0,77 | ||||||
| -3,80 | 0,38 | 0,78 | ||||||
| -3,90 | 0,39 | 0,79 | ||||||
| 0,00 | 0,5000 | 0,40 | 0,6554 | 0,80 | 0,7881 | |||
| 0,01 | 0,41 | 0,81 | ||||||
| 0,02 | 0,42 | 0,82 | ||||||
| 0,03 | 0,43 | 0,83 | ||||||
| 0,04 | 0,44 | 0,84 | ||||||
| 0,05 | 0,45 | 0,85 | ||||||
| 0,06 | 0,46 | 0,86 | ||||||
| 0,07 | 0,47 | 0,87 | ||||||
| 0,08 | 0,48 | 0,88 | ||||||
| 0,09 | 0,49 | 0,89 | ||||||
| 0,10 | 0,5398 | 0,50 | 0,6915 | 0,90 | 0,8159 | |||
| 0,11 | 0,51 | 0,91 | ||||||
| 0,12 | 0,52 | 0,92 | ||||||
| 0,13 | 0,53 | 0,93 | ||||||
| 0,14 | 0,54 | 0,94 | ||||||
| 0,15 | 0,55 | 0,95 | ||||||
| 0,16 | 0,56 | 0,96 | ||||||
| 0,17 | 0,57 | 0,97 | ||||||
| 0,18 | 0,58 | 0,98 | ||||||
| 0,19 | 0,59 | 0,99 | ||||||
| 0,20 | 0,5793 | 0,60 | 0,7257 | 1,00 | 0,8413 | |||
| 0,21 | 0,61 | 1,01 | ||||||
| 0,22 | 0,62 | 1,02 | ||||||
| 0,23 | 0,63 | 1,03 | ||||||
| 0,24 | 0,64 | 1,04 | ||||||
| 0,25 | 0,65 | 1,05 | ||||||
| 0,26 | 0,66 | 1,06 | ||||||
| 0,27 | 0,67 | 1,07 | ||||||
| 0,28 | 0,68 | 1,08 | ||||||
| 0,29 | 0,69 | 1,09 | ||||||

| 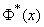
| 
| 
| 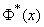
| 
| 
| 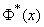
| 
|
| 1,10 | 0,8643 | 1,50 | 0,9332 | 1,90 | 0,9713 | |||
| 1,11 | 1,51 | 1,91 | ||||||
| 1,12 | 1,52 | 1,92 | ||||||
| 1,13 | 1,53 | 1,93 | ||||||
| 1,14 | 1,54 | 1,94 | ||||||
| 1,15 | 1,55 | 1,95 | ||||||
| 1,16 | 1,56 | 1,96 | ||||||
| 1,17 | 1,57 | 1,97 | ||||||
| 1,18 | 1,58 | 1,98 | ||||||
| 1,19 | 1,59 | 1,99 | ||||||
| 1,20 | 0,8849 | 1,60 | 0,9452 | 2,00 | 0,9772 | |||
| 1,21 | 1,61 | 2,10 | ||||||
| 1,22 | 1,62 | 2,20 | ||||||
| 1,23 | 1,63 | 2,30 | ||||||
| 1,24 | 1,64 | 2,40 | ||||||
| 1,25 | 1,65 | 2,50 | ||||||
| 1,26 | 1,66 | 2,60 | ||||||
| 1,27 | 1,67 | 2,70 | ||||||
| 1,28 | 1,68 | 2,80 | ||||||
| 1,29 | 1,69 | 2,90 | ||||||
| 1,30 | 0,9032 | 1,70 | 0,9554 | 3,00 | 0,9986 | |||
| 1,31 | 1,71 | 3,10 | ||||||
| 1,32 | 1,72 | 3,20 | ||||||
| 1,33 | 1,73 | 3,30 | ||||||
| 1,34 | 1,74 | 3,40 | ||||||
| 1,35 | 1,75 | 3,50 | ||||||
| 1,36 | 1,76 | 3,60 | ||||||
| 1,37 | 1,77 | 3,70 | ||||||
| 1,38 | 1,78 | 3,80 | ||||||
| 1,39 | 1,79 | 3,90 | 1,0000 | |||||
| 1,40 | 0,9192 | 1,80 | 0,9641 | |||||
| 1,41 | 1,81 | |||||||
| 1,42 | 1,82 | |||||||
| 1,43 | 1,83 | |||||||
| 1,44 | 1,84 | |||||||
| 1,45 | 1,85 | |||||||
| 1,46 | 1,86 | |||||||
| 1,47 | 1,87 | |||||||
| 1,48 | 1,88 | |||||||
| 1,49 | 1,89 |
|
|
|
|
|
|
|
|
|
Таблица 2. Значения экспоненциальной функции 

| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
|
| 0,00 | 1,000 | 0,40 | 0,670 | 0,80 | 0,449 | 3,00 | 0,050 | ||||
| 0,01 | 0,990 | 0,41 | 0,664 | 0,81 | 0,445 | 3,10 | 0,045 | ||||
| 3,20 | |||||||||||
| 3,30 | |||||||||||
| 3,40 | |||||||||||
| 3,50 | |||||||||||
| 3,60 | |||||||||||
| 3,70 | |||||||||||
| 3,80 | |||||||||||
| 3,90 | |||||||||||
| 0,10 | 0,905 | 0,50 | 0,606 | 0,90 | 0,407 | 4,00 | 0,0183 | ||||
| 4,10 | |||||||||||
| 4,20 | |||||||||||
| 4,30 | |||||||||||
| 4,40 | |||||||||||
| 4,50 | |||||||||||
| 4,60 | |||||||||||
| 4,70 | 0,0091 | ||||||||||
| 4,80 | |||||||||||
| 4,90 | |||||||||||
| 0,20 | 0,819 | 0,60 | 0,549 | 1,00 | 0,368 | 5,00 | 0,0067 | ||||
| 1,10 | 5,10 | ||||||||||
| 1,20 | 5,20 | ||||||||||
| 1,30 | 5,30 | ||||||||||
| 1,40 | 5,40 | ||||||||||
| 1,50 | 5,50 | ||||||||||
| 1,60 | 5,60 | ||||||||||
| 1,70 | 5,70 | ||||||||||
| 1,80 | 5,80 | ||||||||||
| 1,90 | 5,90 | ||||||||||
| 0,30 | 0,741 | 0,70 | 0,497 | 2,00 | 0,135 | 6,00 | 0,0025 | ||||
| 2,10 | 6,10 | ||||||||||
| 2,20 | 6,20 | ||||||||||
| 2,30 | 6,30 | ||||||||||
| 2,40 | 0,091 | 6,40 | |||||||||
| 2,50 | 6,50 | ||||||||||
| 2,60 | 6,60 | ||||||||||
| 2,70 | 6,70 | ||||||||||
| 2,80 | 6,80 | ||||||||||
| 2,90 | 6,90 | ||||||||||
| 0,40 | 0,670 | 0,80 | 0,449 | 3,00 | 0,050 | 7,00 | 0,0009 |
|
|
|
Таблица 3. Значения нормальной функции 

| 
| ||||||||||
| 0,0 | 0,3989 | 0,0 | |||||||||
| 0,1 | 0,1 | ||||||||||
| 0,2 | 0,2 | ||||||||||
| 0,3 | 0,3 | ||||||||||
| 0,4 | 0,4 | ||||||||||
| 0,5 | 0,5 | ||||||||||
| 0,6 | 0,6 | ||||||||||
| 0,7 | 0,7 | ||||||||||
| 0,8 | 0,8 | ||||||||||
| 0,9 | 0,9 | ||||||||||
| 1,0 | 0,2420 | 1,0 | |||||||||
| 1,1 | 1,1 | ||||||||||
| 1,2 | 1,2 | ||||||||||
| 1,3 | 1,3 | ||||||||||
| 1,4 | 1,4 | ||||||||||
| 1,5 | 1,5 | ||||||||||
| 1,6 | 1,6 | ||||||||||
| 1,7 | 1,7 | ||||||||||
| 1,8 | 1,8 | ||||||||||
| 1,9 | 1,9 | ||||||||||
| 2,0 | 0,0540 | 2,0 | |||||||||
| 2,1 | 2,1 | ||||||||||
| 2,2 | 2,2 | ||||||||||
| 2,3 | 2,3 | ||||||||||
| 2,4 | 2,4 | ||||||||||
| 2,5 | 2,5 | ||||||||||
| 2,6 | 2,6 | ||||||||||
| 2,7 | 2,7 | ||||||||||
| 2,8 | 2,8 | ||||||||||
| 2,9 | 2,9 | ||||||||||
| 3,0 | 0,0044 | 3,0 | |||||||||
| 3,1 | 3,1 | ||||||||||
| 3,2 | 3,2 | ||||||||||
| 3,3 | 3,3 | ||||||||||
| 3,4 | 3,4 | ||||||||||
| 3,5 | 3,5 | ||||||||||
| 3,6 | 3,6 | ||||||||||
| 3,7 | 3,7 | ||||||||||
| 3,8 | 3,8 | ||||||||||
| 3,9 | 3,9 | ||||||||||

| 
|
Таблица 4. Значения  в зависимости от
в зависимости от  и
и 


| 0,99 | 0,98 | 0,95 | 0,90 | 0,80 | 0,70 | 0,50 | 0,30 | 0,20 | 0,10 | 0,05 | 0,02 | 0,01 | 0,001 |
| 0,000 | 0,001 | 0,004 | 0,016 | 0,064 | 0,148 | 0,455 | 1,074 | 1,642 | 2,71 | 3,84 | 5,41 | 6,64 | 10,83 | |
| 0,020 | 0,040 | 0,103 | 0,211 | 0,446 | 0,713 | 1,386
Воспользуйтесь поиском по сайту:  ©2015 - 2026 megalektsii.ru Все авторские права принадлежат авторам лекционных материалов. Обратная связь с нами...
|

