Тема 6. Показатели вариации

Понятие вариации признака и значение ее статистического изучения

Вариацией признака называется наличие различий в численных значениях какого-либо признака внутри совокупности. Причиной колеблемости признаков является множественность действующих факторов. Среди значительного числа факторов всегда найдется один или несколько, которые не останутся постоянными, что неизбежно скажется на общем итоге их влияния, а следовательно, и на признаках изучаемых явлений.

Показатели вариации изучаются для решения вполне определенных задач, одной из которых является оценка типичности средней величины.

Как известно, средняя величина лишь в том случае может считаться инструментом научного исследования, когда она исчислена для однокачественных единиц. В противном случае она является огульной средней и непригодной для статистического анализа. Оценка типичности средней – это и оценка однородности совокупности, для которой она исчислена. Представление об отклонении индивидуальных значений от средней и дают показатели вариации.

Размах вариации – это амплитуда колебания, определяется как разность между экстремальными значениями вариационного ряда . Размах вариации является величиной неустойчивой и не может в полной мере охарактеризовать колеблемость ряда по двум причинам:

1) не учитывает промежуточных значений вариант внутри крайних пределов, а поэтому не отражает колеблемость ряда в целом;

2) основываясь только на двух значениях, которые могут оказаться недостаточно характерными, может отражать случайную, а не типичную для данного ряда величину колеблемости.

Вариационный размах имеет и самостоятельное значение. Например, в промышленности допуски точности изготовляемых изделий устанавливаются в определенных пределах, что соответствует величине размаха вариации их признаков. В судоходстве показатели крайних значений глубины судоходных путей являются предельной границей для пропуска судов с соответствующими осадками.

Последующие показатели вариации являются логическим следствием поиска устранения недостатков размаха вариации и более точной характеристики колеблемости признаков по сравнению с типическим уровнем – со средней величиной, как эталоном.

Стремление ослабить влияние случайных факторов приводит к расчету среднего линейного отклонения. Это отклонение определяется как средняя арифметическая из абсолютных значений отклонений индивидуальных значений признака от средней величины. Для сгруппированных данных расчет ведется по формуле:

.

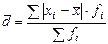Для несгруппированных данных применяется формула:

.

При расчете среднего линейного отклонения во внимание принимаются все без исключения элементы ряда. Однако это улучшение достигается посредством нарушения элементарных правил математики (отбрасываются знаки, т.к. сумма отклонений индивидуальных значений от средней равна нулю).

Широкое распространение получил показатель дисперсия – средняя величина из квадратов отклонений от средней 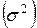, расчет ее производится по ниже приведенным формулам соответственно для сгруппированных

и несгруппированных данных:

.

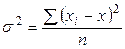Дисперсия широко применяется в разного рода расчетах. Однако она не совсем удобна, т.е. является величиной неименованной в отличии от средней величины, что препятствует их сравнению. Чтобы устранить это препятствие из дисперсии извлекают квадратный корень и получают среднее квадратическое отклонение :

 

.

 

Среднее квадратическое отклонение используется для сопоставления вариации признака по нескольким однородным совокупностям или одной совокупности за разные годы. Например, исчисленная средняя себестоимость единицы продукции объединения в отчетном году по сравнению с прошлым годом снизилась, а среднее квадратическое отклонение возросло. Это говорит о том, что снижение средней себестоимости нельзя считать удовлетворительным, т.к. имеются существенные различия в себестоимости продукции передовых и отстающих предприятий данного объединения.

Среднее квадратическое отклонение является мерилом надежности средней. Чем ниже среднее квадратическое отклонение, тем типичнее средняя величина.

Среднее квадратическое отклонение является величиной именованной, поэтому его нельзя использовать в целях сопоставимости вариации средней выработки и средней заработной платы рабочих предприятия. Для достижения сопоставимости показателей вариации принято исчислять коэффициент вариации :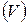

.

Т.е. коэффициент вариации – это процентное отношение среднего квадратического отклонения к средней величине.

Данный показатель применяется и тогда, когда дается сравнительная характеристика колеблемости одного и того же признака у разных совокупностей, например, сравнение размеров колеблемости урожайности различных культур, уровней производительности труда рабочих, занятых производством различных видов продукции.

Критическое значение коэффициента вариации – 35%. Совокупность можно считать более или менее однородной, а среднюю – типичной, если коэффициент вариации не более 35%. Если же коэффициент вариации равен или более 35%, то совокупность неоднородна, а средняя является огульной.

Рассмотрим пример расчета показателей вариации.

Урожайность пшеницы характеризуется следующими данными:

Таблица 6.1

 

Урожайность	Посевная площадь, га	Середина интервала
14-16
16-18
18-20
20-22
Итого		Х

 

Определим: 1) среднюю урожайность:

 

ц;

 

2) размах вариации:

 

ц;

 

3) среднее линейное отклонение:

 

4) дисперсию:

 

5) среднее квадратическое отклонение:

 

ц;

 

6) коэффициент вариации:

 

.

 

Таким образом, индивидуальная урожайность на отдельных участках колеблется от средней урожайности в среднем на 1,8 ц или 9,8%.

Между показателями вариации имеются определенные соотношения, знание которых позволяет переходить от одного показателя колеблемости к другому, не затрачивая существенных усилий на расчеты. Такой переход бывает необходим при решении ряда практических задач. Например, при некоторых способах статистического контроля устойчивости производственного процесса такие переходы от одного показателя к другому могут быть полезны.

Зная соотношение между различными показателями вариации можно находить приблизительную величину сложно исчисляемых показателей более просто, например, величину среднего квадратического отклонения исходя из размаха вариации:

 

.

 

Соотношение между другими показателями вариации таково:

 

точнее

 

или

 

точнее .

 

Данные соотношения будут тем точнее, чем больше объем совокупности, а распределение ее ближе к нормальному.

⇐ Предыдущая234567891011Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: