Выявление основной тенденции ряда динамики

Выявление основной тенденции развития (тренда) динамического ряда предполагает ее количественное выражение, в определенной мере свободное от случайных воздействий. Выявление основной закономерности осуществляется методами выравнивания.

Наиболее простым приемом обнаружения общей тенденции развития явления является укрупнение интервала динамического ряда. Суть этого приема состоит в том, что исходный ряд динамики заменяется другим, уровни которого относятся к большим по продолжительности периодам времени.

Вновь образованный ряд может содержать или абсолютные или средние величины, в которых взаимопогашаются случайные отклонения и обнаруживается основная линия развития, обусловленная действием основных факторов.

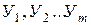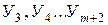При выявлении основной тенденции методом скользящей средней по-особому укрупняются интервалы времени. Каждый последующий интервал получают постепенно сдвигаясь от начального уровня динамического ряда на один уровень. Так первый интервал будет включать уровни ; второй уровни ; третий – и т. д.

Таким образом, скользящая средняя – это подвижная динамическая средняя, которая подсчитывается по динамическому ряду при последовательном передвижении на один срок. По укрупненным интервалам рассчитывается скользящая средняя, которая относится к середине укрупненного интервала. Если же интервал берется по четному числу уровней, то производится центрирование, т. е. нахождение средней из средних для отнесения полученного уровня, к отдельному моменту (периоду) времени.

Проиллюстрируем эти два приема нахождения основной тенденции ряда на числовом примере.

Таблица 7.13

 

Годы	1990г	1991г	1992г	1993г	1994г	1995г	1996г	1997г	1999г
% ракрыт. преступл.	67,6		70,1	74,8	78,1	76,6	78,1	77,9	78,8

 

Способ укрупнения интервалов.

В качестве укрупненного интервала возьмем три года и рассчитаем процент раскрываемости преступлений в среднем за каждое трехлетие:

1990-1992 г.г. (67,6+67+70,1):3=68,2%,

1993-1995 г.г. (74,.8+78,1+76,6):3=76,5%,

1996-1998 г.г. (78,1+77,9+78,8):3=78,3%.

Недостатком рассмотренного способа является то, что при его использовании из поля зрения выпадает процесс изменения внутри укрупненных интервалов.

Способ скользящей средней.

Продолжительность периода, который включается в расчет при исчислении скользящей средней также возьмем равным трем годам:

 

1991г. (67,6+67+70,1):3=68,2,

1992г. (67+70,1+74,8):3=70,6,

1993г. (70,1+74,8+78,1):3=74,,3

1994г. (74,8+78,1+76,6):3=76,5,

1995г. (78,1+76,6+78,1):3=77,6,

1996г. (76,6+78,1+77,9):3=77,5,

1997г. (78,1+77,9+78,8):3=78,3.

Скользящая средняя действительно помогла более отчетливо выявить тенденции в развитии изучаемого показателя.

Возникает вопрос какой период укрупнения интервала (скользящей средней) следует брать? Если в изучаемом ряду динамики имеются периодические колебания, то период скользящей средней (укрупненный интервал) следует брать равным периоду (циклу колебания). Если в ряду периодические колебания отсутствуют, то период скользящей или ступенчатой средней начинают с наименьшего возможного укрупненного интервала (у нас – двухгодичного). При необходимости (в тех случаях когда тенденция сразу не выявляется) переходят к следующему возможному интервалу до тех пор, пока не будет более или менее ясно выступать тенденция развития.

Наиболее эффективным способом выявления основной тенденции развития является аналитическое выравнивание ряда динамики. Суть выравнивания состоит в том, что исходные данные могут быть приближенно выражены определенным математическим уравнением, которое подбирается на основе теоретического анализа. При аналитическом выравнивании ряда динамики закономерно изменяющийся уровень изучаемого показателя оценивается как функция времени . Чаще всего при выравнивании используются линейная, параболическая, экспоненциальная зависимости.

Линейная зависимость выбирается в тех случаях, когда в исходном временном ряду наблюдаются более или менее постоянные абсолютные цепные приросты, не проявляющие тенденции ни к увеличению, ни к снижению.

Параболическая зависимость используется, если абсолютные цепные приросты сами по себе не обнаруживают некоторую тенденцию развития, но абсолютные цепные приросты абсолютных цепных приростов (разности второго порядка) никакой тенденции развития не проявляют.

Экспоненциальные зависимости применяются, если в исходном временном ряду наблюдается более или менее постоянный относительный рост (устойчивость цепных темпов роста, темпов прироста, коэффициентов роста).

Чаще всего на практике приходится иметь дело с выравниванием по прямой.

Применительно к динамическим данным уравнение прямой можно записать так:

,

где 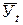- ординаты прямой, т. е. выравненные уровни ряда;

t – порядковый номер периода или момента времени, к которому относятся данные;

а и в – параметры прямой.

Параметры а и в рассчитываются по методу наименьших квадратов:

 

В целях упрощения расчетов параметров а и в систему можно упростить. Для этого отсчет времени следует вести так, чтобы сумма показателей времени ряда была равна нулю. В этом случае при нечетном числе уровней ряда динамики, уровень находящийся в середине ряда, принимается за условное начало отсчета времени (этому периоду или моменту времени придается нулевое значение). Даты времени, стоящие выше этого уровня, обозначаются натуральными числами со знаком минус (-1, -2, -3 и т.д.), а ниже – со знаком плюс (+1, +2, +3 и т.д.) (см. гр 3. табл. 7.14).

Если число уровней ряда четное, рекомендуется обозначить периоды верхней половины ряда (от середины) –1, -3, -5 и т. д., а нижней половины +1,+3,+5 и т. д.

При условии, что , система нормальных уравнений принимает вид:

,

откуда .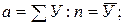

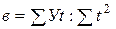Выравняем ряд динамики раскрываемости преступлений по прямой, для чего расчет параметров уравнения произведем в таб. 7.14.

Таблица 7.14

 

Годы	% раскрываемости преступлений, У	t	Уt		Выравненные уровни ряда
	67,6	-4	-270,4		67,98
		-3	-201		69,57
Продолжение табл. 7.14
	70,1	-2	-140,2		71,16
	74,8	-1	-74,8		72,74
	78,1				74,33
	76,6	+1	+76,6		75,93
	78,1	+2	+156,2		77,52
	77,9	+3	+233,7		79,09
	78,8	+4	+315,2		80,68
Итого			+95,3

 

Используя итоги граф 2,4,5 определим параметры уравнения прямой:

а = 669:9=74,33; в = 95,3:60=1,588

Записываем уравнение прямой:

 

.

 

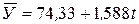Подставляя значение t (гр3 табл. 7.14) рассчитаем для каждого года теоретические значения:

1990г.

1991г. и т. д. (см гр. 6 табл. 7.14).

Правильность расчета уровней выравненного ряда динамики может быть проверена следующим образом: сумма значений эмпирического ряда (итог гр. 2) должна совпадать с суммой выравненных уровней (итог гр. 6): .

Нахождение значений ряда динамики для последующих периодов на основе тенденции, наблюдавшейся в прошлом, называется экстраполяцией. По данным уравнения прямой можно экстраполировать уровни для последующих лет. Так, если подставить в уравнение значение t=5, можно найти уровень раскрываемости преступлений в 1999 г. равный 82,47%.

Возможность проведения экстраполяции основана на следующих положениях:

1) Общие условия, определяющие тенденцию развития в прошлом, не претерпевают существенных изменений в будущем;

2) тенденция развития явления характеризуется тем или иным аналитическим уравнением.

Значение , полученное в результате экстраполяции, используют для определения прогнозного значения на будущее.

Тема 8. Выборочный метод

⇐ Предыдущая567891011121314Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: