 |
Показатели ряда динамики и методы их расчета
|
|
|
|
Для характеристики скорости и интенсивности изменения уровней ряда динамики рассчитывается система цепных и базисных показателей.
Показатели динамики с переменной базой (цепные показатели) характеризуют интенсивность изменения уровня от периода к периоду (или от даты к дате).
Показатели динамики с постоянной базой (базисные показатели) характеризуют окончательный результат всех изменений в уровнях ряда от периода, к которому относятся базисный уровень, до данного (i-того) периода.
В результате такого сравнения вычисляют систему показателей, в которую включаются абсолютный прирост, коэффициент роста, темп роста, темп прироста и абсолютное значение одного процента прироста.
Абсолютный прирост (D) определяется как разность между двумя уровнями динамического ряда и показывает на сколько данный уровень ряда превышает уровень, принятый за базу сравнения.
Базисный абсолютный прирост вычисляется по формуле:
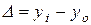 .
.
Цепной абсолютный прирост будет равен:
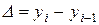 .
.
В этих формулах 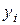 - уровень сравниваемого периода,
- уровень сравниваемого периода, 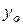 – уровень базисного периода,
– уровень базисного периода,  - – уровень предшествующего периода.
- – уровень предшествующего периода.
Коэффициент роста (К) определяется как отношение двух сравниваемых уровней и показывает, во сколько раз данный уровень превышает уровень, принятый за базу сопоставления.
При сравнении с постоянной базой
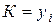 :
: 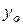 .
.
При сравнении с переменной базой
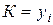 :
: 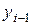 .
.
Коэффициенты роста, выраженные в процентах, называются темпами роста:
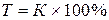 .
.
Темп прироста (t) показывает на сколько процентов уровень данного периода больше (или меньше) уровня, взятого за базу сравнения. Этот показатель может быть рассчитан двояко:
как разность между темпом роста и 100%.
|
|
|
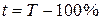 ,
,
2) как отношение абсолютного прироста к уровню, принятому за базу сравнения
 (базисный), или
(базисный), или
 (цепной).
(цепной).
Абсолютное значение одного процента прироста (А) рассчитывается делением абсолютного прироста на темп прироста. Этот показатель вычисляется только как цепной.
 .
.
Если эту формулу преобразовать, то получим следующее выражение:
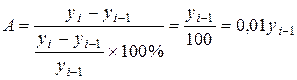 .
.
Для обобщающей характеристики динамики уровней определяют:
1)средние уровни ряда;
2) средние показатели изменения уровней.
Для моментного ряда динамики средний уровень вычисляют по формуле средней хронологической (если промежутки времени между датами одинаковы)
 ,
,
где 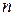 – число уровней ряда,
– число уровней ряда,
 – уровни ряда
– уровни ряда
Если промежутки времени между датами различны, то средний уровень определяется по формуле средней арифметической взвешенной, а в качестве веса (t) берется продолжительность времени между датами ( ).
).
Для периодического (интервального) ряда динамики средний уровень ряда рассчитывается по формуле средней арифметической простой:
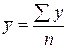 .
.
Средний коэффициент роста определяется по формуле средней геометрической:
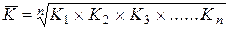 или
или 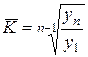 ,
,
где K1, K2, K3, ….. Kn- цепные коэффициенты роста,
средний темп роста: 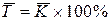 ,
,
средний темп прироста: 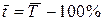 .
.
Проведем расчеты изложенных показателей по данным табл. 7.7.
Таблица 7.7
| Годы | 1995 г. | 1996 г. | 1997 г. | 1998 г. | 1999 г. |
| Количество преступлений на 100 тыс. населения. | 2 800 | 3 105 | 3 318 | 3 456 | 3 497 |
Динамика преступности в районе
| Абсолютные приросты: | |
| цепные | базисные |
| 3 105-2 800=+305, | 3 105-2 800=+305, |
| 3 318-3 105=+213, | 3 318-2 800=+518, |
| 3 456-3 318=+138, | 3 456-2 800=+565, |
| 3 497-3 456=+41. | 3 497-2 800=+697. |
Коэффициент частоты преступлений по сравнению с первым уровнем ряда (1995 г.) ежегодно значительно возрастает, а по сравнению с каждым предшествующим годом рост снижается.
| Коэффициенты роста: | |
| цепные | базисные |
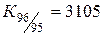 : : 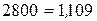 , ,
| 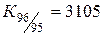 : : 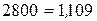 , ,
|
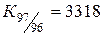 :1,069, :1,069,
|  :2 800=1,185, :2 800=1,185,
|
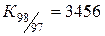 :3 318=1,042, :3 318=1,042,
| 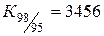 :2 800=1,234, :2 800=1,234,
|
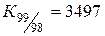 :3 456=1,012. :3 456=1,012.
| 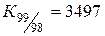 :2 800=1,249. :2 800=1,249.
|
Здесь коэффициент 1,012 показывает, что количество преступлений на 100 тыс. населения в 1999 г. возросло по сравнению с 1998 г. в 1,012 раза, а коэффициент 1,249 говорит о том, что количество преступлений в 1999г. по сравнению с 1995г. возросло в 1,249 раза и т. п.
|
|
|
| Темпы роста: | |
| цепные | базисные |
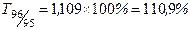 , ,
|  , ,
|
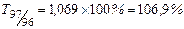 , ,
| 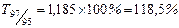 , ,
|
 , ,
| 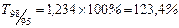 , ,
|
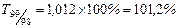 . .
| 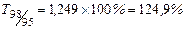 . .
|
Наблюдается снижение цепных темпов роста уровня преступности и рост базисных темпов роста.
| Темпы прироста: | |
| цепные | базисные |
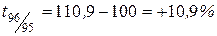 , ,
| 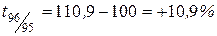 , ,
|
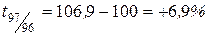 , ,
| 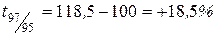 , ,
|
 , ,
| 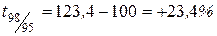 , ,
|
 . .
|  . .
|
Следовательно, уровень преступности в 1999 г. по сравнению с 1998 г. возрос на 1,2%, а по сравнению с 1995 г. на 24,9% и т. д.
Абсолютное значение 1% прироста:
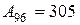 :10,9=28 или 2 800:100=28,
:10,9=28 или 2 800:100=28,
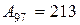 :6,9=31 или 3 105:100=31,
:6,9=31 или 3 105:100=31,
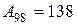 :4,2=33 или 3 318:100=33,
:4,2=33 или 3 318:100=33,
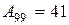 :1,2=34 или 3 456:100=34.
:1,2=34 или 3 456:100=34.
Среднегодовой коэффициент роста:
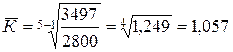 .
.
В среднем за 1995-1999 годы уровень преступности возрастал ежегодно в 1, 057 раза.
Среднегодовой темп роста:
 .
.
Среднегодовой темп прироста:
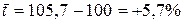 .
.
В среднем уровень преступности ежегодно возрастал на 5,7%.
Средний уровень преступности за 1995-1999 г. г. составил:

преступлений на 100 тыс. человек населения района.
Измерение сезонности
Уровни рядов динамики, слагаясь под совместным влиянием систематических и случайных факторов, иногда испытывают воздействие причин, обусловленных периодичностью колебаний. Сезонные колебания – это внутригодичные колебания уровней динамического ряда. Они выражаются в том, что в отдельные месяцы года уровни возрастают, в другие – снижаются. Потребление энергии, перевозки пассажиров, спрос на отдельные виды продукции, например, носят сезонный характер. Сезонные колебания характерны и для ряда показателей правовой статистики: поступление жилищных дел в суды, имущественные преступления, преступления против личности.
Для измерения сезонных колебаний статистикой предложены различные методы, одним из которых является построение индексов сезонности.
Наиболее простой прием расчета индексов сезонности в рядах динамики, которые обнаруживают тенденцию к росту или снижению уровней за каждый месяц по годам состоит в том, что данные за отдельные месяцы соотносятся со среднемесячным уровнем данного года, а затем из полученных по каждому месяцу величин исчисляется средняя арифметическая. Этот метод расчета индексов сезонности изложен в табл. 7.8.
|
|
|
Среднемесячный уровень за 1997, 1998, 1999 г.г. определяется делением годового количества преступлений на 12 месяцев. А затем уровень каждого месяца относится к среднемесячному уровню соответствующего года. Результаты этих расчетов, выраженные в процентах, отражены в графах 5, 6, 7 табл. 7.8.
Индексы же сезонности определяются как величина средняя арифметическая простая из помесячных данных.
За январь: (74,6+74,2+73,9):3=74,2%, за февраль:
За февраль: (77,9+77,4+77):3=77,4% и т. д.
Для количественного измерения силы сезонных колебаний применяются показатели вариации.
Приближенное представление о мере сезонности дает размах вариации колебаний, который вычисляется по каждому ряду динамики. Его расчет осуществляется, вычитанием из максимального индекса сезонности минимального индекса.
Таблица 7.8
| Месяц | Абсолютные уровни | в % к среднемесячному уровню. | Индексы сезонности | |||||
| 1997г. | 1998г. | 1999г. | 1997г | 1998г. | 1999г. | |||
| I | 74,6 | 74,2 | 73,9 | 74,2 | ||||
| II | 77,9 | 77,4 | 77,0 | 77,4 | ||||
| III | 88,1 | 90,9 | 88,8 | 89,3 | ||||
| IY | 97,7 | 96,8 | 98,5 | 97,7 | ||||
| Y | 107,9 | 112,4 | 115,3 | 111,9 | ||||
| YI | 116,9 | 113,.9 | 117,3 | 116,0 | ||||
| YII | 121,5 | 120,4 | 126,5 | 122,8 | ||||
| YIII | 119,2 | 123,6 | 119,9 | 120,9 | ||||
| IX | 117,5 | 115,6 | 112,7 | 115,3 | ||||
| X | 103,9 | 101,6 | 102,0 | 102,5 | ||||
| XI | 97,2 | 95,2 | 91,3 | 94,6 | ||||
| XII | 80,2 | 79,6 | 77,5 | 79,1 | ||||
| Продолжение табл. 7.8 | ||||||||
| В сренем. за месяц | ||||||||
Например, по данным таб. 7.8 размахи колебаний составили:
1997 г. 121,5-74,6=46,9%.
1998 г. 123,6-74,2=49,4%.
1999 г. 126,5-73,5=52,6%..
Сравнение размахов колебаний за несколько лет позволяет судить о направлении в изменении сезонности. Так по данным нашего расчета видно что происходит усиление сезонных колебаний.
Однако размах вариации не дает полного представления о глубине сезонных колебаний, т. к. опирается только на два экстремальных значения индексов сезонности.
|
|
|
Поэтому рассчитывается коэффициент сезонности колеблемости методом среднего квадратического отклонения:
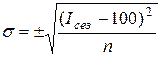 .
.
Для нашего примера:
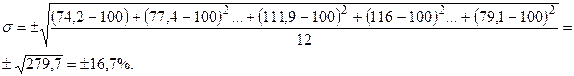
При исчислении показателей колеблемости из сезонной волны (индексов сезонности) среднее квадратическое отклонениетождественно коэффициенту вариации, т. к. средней величиной для индексов сезонности является 100.
Сравнение коэффициентов сезонности, вычисленных за несколько периодов, покажет сдвиги в сезонности. Если эти показатели уменьшаются, значит сезонный характер преступности идет на убыль.
Рассмотрим вычисление сезонной волны в стабильном ряду динамики, в котором нет ярко выраженной тенденции к росту или снижению, когда внутригодичные колебания происходят вокруг некоторого постоянного уровня –  . Индексы сезонности в этом случае исчисляются по формуле:
. Индексы сезонности в этом случае исчисляются по формуле:
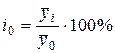 (2.1.1)
(2.1.1)
где  – средняя из фактических уровней одноименных месяцев;
– средняя из фактических уровней одноименных месяцев;
 – общая средняя за исследуемый период.
– общая средняя за исследуемый период.
Рассчитаем индексы сезонности по данным о перевозке грузов автотранспортным предприятием за три года (см. табл. 7.9.).
Как видно из приведенных данных, ярко выраженной тенденции к росту или снижению объема перевозок в ряду динамики не наблюдается.
Индексы сезонности исчисляются в три этапа:
1. Рассчитываются среднемесячные уровни перевозок ( ) поданным за три года по формуле средней арифметической простой (гр.6 = гр. 5: 3). Это позволяет избавиться от случайных колебаний месячных уровней.
) поданным за три года по формуле средней арифметической простой (гр.6 = гр. 5: 3). Это позволяет избавиться от случайных колебаний месячных уровней.
Таблица 7.9
| Месяц | Объем перевозок, тыс. т | Индексы сезонности, % | ||||
| 1-й год | 2-й год | 3-й год | Всего за 3 года | В среднем за 3 года | ||
| январь | 94,8 | |||||
| февраль | 95,7 | |||||
| март | 98,4 | |||||
| апрель | 101,1 | |||||
| май | 102,1 | |||||
| июнь | 103,9 | |||||
| июль | 105,7 | |||||
| август | 109,3 | |||||
| сентябрь | 104,8 | |||||
| октябрь | 98,4 | |||||
| ноябрь | 93,8 | |||||
| декабрь | 92,9 | |||||
| Итого | 1097,5 | 100,0 |
2. Определяется общая средняя за исследуемый период ( ) делением общего итога графы 5 на 36 месяцев (39510: 36 = 1097,5).
) делением общего итога графы 5 на 36 месяцев (39510: 36 = 1097,5).
3. Исчисляются индексы сезонности, которые представлены в графе 7 табл. 7.9.
Рассмотрим анализ сезонных колебаний по методу Персонса
Измерение сезонности методом У. Персонса применяется в рядах динамики, отражающих развитие явлений, общая тенденция которых изменяется по средней геометрической, т.е. по сложным процентам. Суть метода У.Персонса заключается в исчислении показателей средней сезонной волны как медианных значений (а не как простых средних арифметических) из цепных отношений. Здесь погрешность, вызванная влиянием общей тенденции, устраняется с помощью среднего коэффициента подъема (или снижения) общей тенденции по средней геометрической. При использовании этого метода первым шагом является вычисление цепных отношений как процентных отношений каждого уровня ряда к уровню ряда предшествующего. Затем исчисляют средние из медианных значений. Медиана за первый отрезок времени принимается за единицу (или 100 %), а для остальных периодов средние исчисляются путем последовательного перемножения медианных средних (см. табл. 7.10.). При перемножении преобразованного медианного значения за четвертый квартал на медианное значение первого квартала должна получиться единица (100,0 %). Однако результат обычно бывает больше единицы или меньше ее, поскольку он отражает действительность, на развитие которой оказывает влияние общая тенденция увеличения или уменьшения.
|
|
|
Таблица 7.10
| Год | I квартал | II квартал | III квартал | IV квартал |
| 1-й | 51,9 | 55,0 | 62,3 | 54,1 |
| 2-й | 48,0 | 48,7 | 48,0 | 46,6 |
| 3-й | 43,0 | 49,6 | 58,4 | 48,0 |
| 4-й | 46,3 | 48,0 | 57,2 | 45,4 |
| 5-й | 40,0 | 40,2 | 47,3 | 35,3 |
| 6-й | 36,4 | 39,1 | 57,6 | 41,7 |
При анализе сезонности методом относительных величин разность теоретического и действительного исключалась равномерно из каждого квартального показателя, а в способе У. Персонса исключение разности основано на применении формулы сложных процентов.
Измерим сезонные колебания по данному методу, используя условные данные о продаже сахара в городе по кварталам за шесть лет, рассчитав на их основе вначале цепные отношения (темпы роста).
Относительные числа сезонности продажи сахара по данным табл. 7.10 рассчитаем в нижеследующей таблице:
Таблица 7.11
| Год | Поквартальные процентные отношения уровней ряда | |||
| I | II | III | IV | |
| 1-й | 100,00 | 92,48 | 113,27 | 86,84 |
| 2-й | 88,72 | 101,46 | 98,56 | 97,08 |
| 3-й | 92,27 | 115,35 | 117,74 | 82,19 |
| 4-й | 96,46 | 108,67 | 112,17 | 79,37 |
| 5-й | 88,11 | 100,5 | 117,66 | 74,63 |
| 6-й | 103,12 | 107,41 | 147,31 | 72,39 |
Определим среднеквартальные показатели как медианные значения из цепных отношений уровней продажи, расположенных по возрастающим значениям, а не по значениям времени возникновения.
Для первого квартала ранжированный ряд цепных отношений будет иметь вид: 88,11; 88,72; 92,27; 96,46; 103,12. Медиана этого ряда – 92,72 – центральный член нечетного числа членов ряда.
Для второго квартала ранжированный ряд цепных отношений следующий: 92,48; 100,5; 101,46; 107,41; 108,67; 115,35. Медиана этого ряда рассчитывается как средняя двух центральных членов ряда четного числа членов (101,46 + 107,41): 2 = 104,435.
Таким же образом определяются медианные значения для третьего и четвертого кварталов из их цепных отношений (см. табл.7.12.)
Таблица 7.12
| Квартал | Медианные значения из цепных отношений | Преобразованные медианные значения | Сезонные колебания (не выправленные) | Сезонная волна в среднем за 6 лет |
| I | 92,720 | 100,000 | 100,000 | 90,8 |
| II | 104,435 | 104,435 | 106,620 | 96,8 |
| III | 117,700 | 122,920 | 128,175 | 116,4 |
| IV | 80,780 | 99,290 | 105,770 | 96,0 |
| Итого: по всем кварталам | 395,635 | 426,645 | 440,565 | 400,0 |
| в среднем за год | 98,910 | 106,660 | 110,140 | 100,0 |
Медианные значения, исчисленные из цепных отношений, необходимо преобразовать в базисные, приняв за основание медиану первого квартала. Значение для второго квартала в отношении к первому уже было установлено – 104,435 %, для третьего квартала оно определяется перемножением показателя второго квартала на медианное значение из цепных отношений третьего квартала(104,435 · 117,7):100; для четвертого квартала – (122,92 ·80,78): 100.
Перемножение преобразованного значения за четвертый квартал на медианное значение первого квартала (99,29 · 92,72):100 =92,06 обнаруживает, что под влиянием общей тенденции развития ряда динамики к снижению, сезонные колебания сдвинулись на –7,94 % (92,06 – 100).
Исправление погрешности по методу У. Персонса (–7,94 %)основано на предположении развития ряда динамики по формуле сложных процентов. Величина ошибки характеризуется ежеквартальным увеличением или уменьшением, вызванным общей тенденцией. Ежеквартальная поправка исчисляется по следующей формуле:
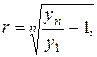
где r – коэффициент поправки;
yn – последний уровень ряда динамики;
y1 – начальный уровень;
n – число уровней.
Для нашего примера эта поправка составит:
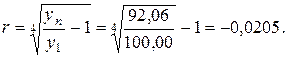
По методу Персонса для исключения общей тенденции, т.е. для того, чтобы выразить только сезонные колебания, необходимо преобразованные медианные значения уменьшить в следующих отношениях: для второго квартала 104,435: 0,9795 = 106,62; для третьего -122,92: (0,9795 - 0,0205) = 122,92: 0,959 = 128,175; для четвертого - 99,29: (0,959 - 0,0205) = 99,29: 0,9385 = 105,77.
Таким образом, исчислены сезонные колебания в чистом виде, но средняя сезонных колебаний составляет 110,14 %, а по выправленной сезонной волне должна быть равной 100 %. Принимая среднюю арифметическую (110,14 %) из исправленных сезонных колебаний за100 %, определяем непосредственно сезонную волну:
для первого квартала 
для второго квартала 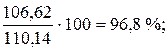
для третьего квартала 
для четвертого квартала 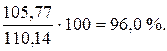
При исчислении средних как медианных значений редкие случайные отклонения не сказываются на индексах сезонности, они не принимаются в расчет. Однако исключение общей тенденции по этому методу производится по сложным процентам, а в действительности же, как было показано выше, развитие ряда динамики может происходить по самым различным траекториям. Поэтому правильнее при анализе сезонности явлений, в которых наблюдается тенденция увеличения или снижения, прежде всего установить форму связи между изменениями времени и уровнями явления, определить общую тенденцию развития явления, исключить ее, а потом уже исчислять показатели сезонности и производить их анализ.
|
|
|


