 |
Какие события называются достоверными и невозможными и каковы их ве-
|
|
|
|
Что называется пространством элементарных событий? Что называется случайным событием? Какие исходы называются благоприятными для события А? Что называется вероятностью события А? Привидите примеры.Можно ли в опыте с бросанием игральной кости считать элементарными следующие события: А – выпадение числа очков, меньших 2; В – выпадение более 2 очков?
Пространством элементарных событий называется множество  , состоящее из исходов или элементарных событий
, состоящее из исходов или элементарных событий  Случайным событием называется любое подмножество пространства элементарных событий А
Случайным событием называется любое подмножество пространства элементарных событий А  , А=
, А=  ,….
,….
И исходы 
 А – благоприятны для события А. Событие А наступило, если в опыте наблюдался один из благоприятных исходов. Вероятностью случайного события А называется отношение числа благоприятных исходов k к общему числу исходов n: P(A) =
А – благоприятны для события А. Событие А наступило, если в опыте наблюдался один из благоприятных исходов. Вероятностью случайного события А называется отношение числа благоприятных исходов k к общему числу исходов n: P(A) =  (в классическом определении вероятности).
(в классическом определении вероятности).
Пример. В опыте с подбрасыванием монеты пространство элементарных событий состоит из двух исходов  =
=  , вероятность выпадания герба А=
, вероятность выпадания герба А= 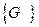 равна P(A)=0.5
равна P(A)=0.5
В опыте с подбрасыванием игральной кости пространство элементарных событий состоит из 6 исходов  =
=  , А-выпадание четного числа, больше 3, т.е. А=
, А-выпадание четного числа, больше 3, т.е. А= 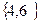 , значит Р(А)=2/6=1/3.
, значит Р(А)=2/6=1/3.
У нас дано, что А – выпаданее меньше 2, а В – выпадание более 2. Т.о. А =  , В=
, В=  . А- это элементарное событие, тк состоит из 1 элементарного события; В – не будет элементарным событием, тк состоит из др. элементарных событий.
. А- это элементарное событие, тк состоит из 1 элементарного события; В – не будет элементарным событием, тк состоит из др. элементарных событий.
Какие события называются достоверными и невозможными и каковы их ве-
роятности? Пусть A, B и C – случайные события. Перечислите все случаи наступления события  .
.
Событие А, которое произойдет при любом испытании, называется достоверным
(А =  ). Например, в опыте с подбрасыванием игральной кости событие А, задаваемое условием “число выпавших очков положительное”, будет достоверным. Вероятность достоверного события равна 1.
). Например, в опыте с подбрасыванием игральной кости событие А, задаваемое условием “число выпавших очков положительное”, будет достоверным. Вероятность достоверного события равна 1.
|
|
|
Событие А, которое не может произойти при испытании, называется невозможным (А=пуст.множ.). Например, событие А, задаваемое условием “при подбрасывании игральной кости выпало 7 очков”, является невозможным. Вероятность невозможного события равна 0.
Таблица, характеризующая событие А  +С
+С
| А | В | С | А  +С +С
|
5.В каком случае событие В называют следствием события А? Какие события называются равными? Объясните, почему  .
.
Событие А влечет за собой событие В или событие В является следствием события А (А  В), если каждый исход, благоприятный для А, является благоприятным и для В. События А и В равны (А=В) в случае, когда они являются следствиями друг друга.
В), если каждый исход, благоприятный для А, является благоприятным и для В. События А и В равны (А=В) в случае, когда они являются следствиями друг друга.
I) А  АВ+А
АВ+А 
Если А наступило(А=1), то: 1) если В при этом наступило, то наступило АВ  АВ+А
АВ+А  наступило; 2) если В не наступило, то
наступило; 2) если В не наступило, то  =1
=1  А
А  =1
=1  АВ+А
АВ+А  наступило.
наступило.
II) АВ+А 
 А
А
Если АВ+А  наступило, то либо АВ наступило (т.е А наступило
наступило, то либо АВ наступило (т.е А наступило  АВ+А
АВ+А 
 А) либо наступило А
А) либо наступило А  (А наступило
(А наступило  АВ+А
АВ+А 
 А).
А).
Событие А наступает, т.к. любое событие А попадает в В или  . А=А(
. А=А( )=А*
)=А*  =А.
=А.
6. Пусть А и В – случайные события. Упростите выражение  . Найдите событие, противоположное событию
. Найдите событие, противоположное событию  .
.
(А+В)(А+  ) = АА+А
) = АА+А  +АВ+В
+АВ+В  =А+А(В+
=А+А(В+  )
)

7. Докажите, что  . Что обозначает событие
. Что обозначает событие  ?
?
 =
=  *
*  *…..*
*…..*  . Наступление события А
. Наступление события А  +….А
+….А  означает, что наступает по меньшей мере одно из событий А
означает, что наступает по меньшей мере одно из событий А  ,….,А
,….,А  . Наступление противоположного события
. Наступление противоположного события  означает, что не наступает ни одно из событий А
означает, что не наступает ни одно из событий А  ,….,А
,….,А  или, по-другому, что наступают одновременно все события
или, по-другому, что наступают одновременно все события  ,….,
,….,  , но это в точности означает наступление события
, но это в точности означает наступление события  *
*  *…..*
*…..*  . Ч.т.д.
. Ч.т.д.
А  А
А 
 + А
+ А 
 А
А  +
+ 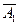 А
А  А
А  : означает наступление ровно двух событий из трех.
: означает наступление ровно двух событий из трех.
|
|
|
8. Докажите, что  =
=  +
+  +…..+
+…..+  . Что означает событие А
. Что означает событие А  А
А  + А
+ А  А
А  + А
+ А  А
А  ?
?
 =
=  +
+  +…..+
+…..+  . Наступление события А
. Наступление события А  *….*А
*….*А  означает, что наступают каждое из событий А
означает, что наступают каждое из событий А  ,….,А
,….,А  . Наступление противоположного события
. Наступление противоположного события  означает, что не наступает хотя бы одно из событий А
означает, что не наступает хотя бы одно из событий А  ,….,А
,….,А  или, по-другому, что наступают события
или, по-другому, что наступают события  +
+  +…..+
+…..+  . Ч.т.д.
. Ч.т.д.
А  А
А  + А
+ А  А
А  + А
+ А  А
А  : означает наступление не меньше двух событий.(или ровно 2 события????????)
: означает наступление не меньше двух событий.(или ровно 2 события????????)
9. Сформулируйте статистическое определение вероятности. Почему вероятность удовлетворяет условию  ? Возможны случаи Р=0 и Р=1? Ответ обоснуйте.
? Возможны случаи Р=0 и Р=1? Ответ обоснуйте.
Вероятность случайного события есть положительное число, заключенное между нулем и единицей. Случайному событию благоприятствует лишь часть из общего числа элементарных исходов испытания. В этом случае 0<m<n, значит, 0<m/n<1, следовательно, 0<P(A)<1. Вероятность любого события удовлетворяет двойному неравенству 0≤Р(А)≤1.
В качестве статистической вероятности события понимают относительную частоту или число, близкое к ней. Свойства вероятностей вытекают из классического определения и сохраняются для статистического.
А – случ.событие
N – кол-во опытов, N 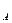 -благ.
-благ.
Р(А)= 
 , где N
, где N 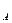
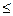 N, N
N, N 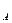
 0.
0.
А- выпала игральная кость, числа которой > 7, P(A)=0
В- выпала игральная кость, числа которой < 7, P(A)=1
|
|
|


