 |
Дисперсия абсолютно непрерывной случайной величины.
|
|
|
|
Дисперсия абсолютно непрерывной случайной величины X с функцией плотности f(x) и матема-тическим ожиданием m = M(X) определяется таким же равенством, как и для дискретной величины
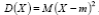
Из равенства (5.26) следует, что справедлива следующая формула
Поскольку формула (5.29) может быть записана в следующем виде
то формулу (5.30) можно представить таким образом
В случае когда абсолютно непрерывная случайная величина X сосредоточена на промежутке [a, b], формулы (5.30), (5.32) примут вид
. 
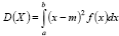Дисперсия непрерывной случайной величины определяет степень рассеивания значений, прини-маемых случайной величиной, вокруг ее математического ожидания.
Среднее квадратичное отклонение, или стандартное отклонение, непрерывной случайной ве-личины X определяется так же, как и для дискретной случайной величины:
4 °. Свойства математического ожидания и дисперсии.
Для математического ожидания и дисперсии непрерывной случайной величины X сохраняются свойства числовых характеристик дискретной случайной величины. Напомним эти свойства.
4. Постоянный множитель выносится из под знака дисперсии в квадрате.
5. Если к случайной величине прибавить константу, то дисперсия не изменится.
6. Дисперсия суммы независимых случайных величин равна сумме дисперсий этих величин.
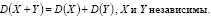
Это не полное т.к. доказать не могу=(
82. Выведите формулу для нахождения мат. ожидания и дисперсии случайной величины, равномерно распределенной на отрезке [a; b].
C.В. Х, сосредоточенная на [a;b], равномерно распределена на этом отрезке, если её функция плотности равна константе: f(х)=с (const), a≤х≤b.
Значение постоянной с определяется из условия: ∫∞-∞ f(х)dх=1, которому удовлетворяет любая плотность вероятности. В данном случае это условие принимает вид: с(b-a)=1, откуда следует, что с=1/(b-a).
|
|
|
М(Х)= ∫ba хf(х)dх= ∫ba сdх, т.к. для абсолютно непрерывной С.В. Х с непрерывной плотностью f(х) М(Х)= ∫ba хf(х)dх.
Т.к. с=1/(b-a), то М(Х)=с*х2/2 |ba = c*(b2-a2)/2=(b+a)/2. Таким образом мы получили, что числу М(Х) соответствует середина [a; b].
Для нахождения дисперсии воспользуемся формулой, где D(Х)= ∫ba х2f(х)dх- m2, где m=M(Х).
D(Х)= 1/(b-a) ∫ba х2dх – ((a+b)/2)2= 1/(b-a)*(b3-a3)/3 - ((a+b)/2)2= (b2+ab+a2)/3 - ((a+b)/2)2= (b-a)2/12.
Таким образом, М(Х)=(b+a)/2, а D(Х)= (b-a)2/12.
83. Объясните (с доказательством) вероятностный смысл параметра m в формуле 
для функции плотности случайной величины Х, распределенной по нормальному закону.
Формула 
описывает плотность нормального распределения вероятностей непрерывной с.в..
Как видно, нормальное распределение определяется двумя параметрами: m и 
. Достаточно знать эти параметры, чтобы задать нормальное распределение. Докажем, что вероятностный смысл этих параметров таков: m есть математическое ожидание.
Поопределению математического ожидания непрерывной с.в.,
Введем новую переменную 
. Отсюда 
. Приняв во внимание, что новые пределы интегрирования равны старым, получим
Первое из слагаемых равно нулю (под знаком интеграла нечетная функция; пределы интегрирования симметричны относительно начала координат). Второе из слагаемых равно m (интеграл Пуассона 
).
Итак, M(X)=m, т.е. математическое ожидание нормального распределения равно параметру m.
84. Объясните (с доказательством) вероятностный смысл параметра σ в формуле для функции плотности 
случайной величины, распределенной по нормальному закону.
Докажем, что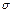 
- среднее квадратическое отклонение нормального распределения. 
Введем новую переменную z==(х—m)/ 
. Отсюда 
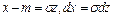. Приняв во внимание, что новые пределы интегрирования равны старым, получим 
Интегрируя по частям, положив u=z, 
найдем 
Следовательно, 
.Итак, среднее квадратическое отклонение нормального распределения равно параметру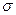 
.
|
|
|
85. Докажите, что для случайной величины, распределенной по показательному закону с параметром 
, математическое ожидание 
Найти числовые характеристики случайной величины X, распределенной по пока-зательному закону с плотностью 
Решение. Для нахождения математического ожидания воспользуемся формулой
M(X)= 
Найдем интеграл методом интегрирования по частям, полагая u = x, dv = e –λ x d (λ x), так что du = dx, v = – e –λ x . Получим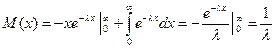 
Таким образом, M(X)= 
86 Случайная величина X равномерно распределена на отрезке [a,b]. Можно ли для любых m и δ>0 подобрать параметры a и b так, чтобы M(x)=m, D(x)=δ2? Как по m и δ найти a и b?
СВ Х, сосред. на [a,b] называется равном. распередёлнной, если её 
на [a,b].
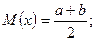
докажем это
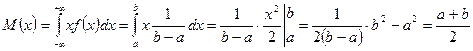
Если M(x)=m, а D(x)= δ2 и m, δ>0 – любые, тогда мы всегда можем подобрать параметры a и b, чтобы выполнялось это условие.
Пример: пусть m=3, δ=4 – тогда 
; 
; 
; 
; 
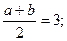
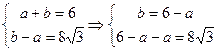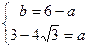87.Что такое правило 
для нормального распределения? Верно ли, что для любой нормальной случайной величины Х существует отрезок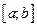 
, для которого 
? Ответ обоснуйте.
Правило трех сигм – отклонение любой случайной величины от ее математического ожидания будет не более трех средних квадратических отклонений (по абсолютной величине). Правило трех сигм применимо для большинства СВ, встречающихся на практике. P (|X-a|<=3сигма) для нормального закона = 0,9973. Для равномерного закона =1. Для показательного = 0,9827 и т.д.
Для нормально распределенной с.в.Х справедлива формула 
Преобразуем эту формулу, приняв 
В итоге получим
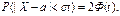
Если t=3 и, следовательн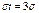о, 
, то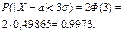 
, т.е. вероятность того, что отклонение по абсолютной величине будет меньше утроенного среднего квадратического отклонения, равна 0,9973.
2. Верно.
88. Формулируйте определение начальных 
моментов случайной величины. Докажите, что если Х и У независимые случайные величины, то 
Начальным моментом порядка k (k принадлежит N), свободная величина Х называется мат.ожиданием k-й степени Х.
Центральным моментом порядка k СВ Х называется мат.ожидание k-й степени отклонения:
Теорема: если Х и У независимые СВ, то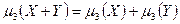 
Док-во:
89. Пусть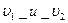 
- начальные, а 
- центральные моменты некоторой случайной величины.
|
|
|
Докажите, что: 
Докажем связь начальных и центральных моментов:
|
|
|
