Перечислите основные свойства функции плотности вероятности. Чем объясняется название «плотность вероятности»?

Св-ва плотности:

1. f(x)
2. 
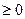
3. во всех точках, где ф-ция плотности непрерывна вып. равенство

f(x)=F’(x)

Поясним смысл назв. «плотность вероят-ти»

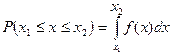
по т. о среднем интеграле, стоящ. в прав. части, равен 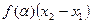, где некоторая точка из инт. .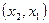

Отсюда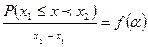

Представим себе, что инт. 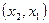, стягив. к некоторой точке 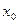, причем в этой точке функция f(x) непрерывна. Тогда будет стремиться к числу f(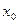), и мы получим:

Отношение, стоящее под знаком предела, есть своего рода «вер-ть на ед-цу длины» интервала 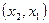. Предел этого отношения рассмотрим как плотность вероятности в самой т. 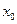. Во всякой т. 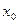, где f(x) непрер., число f(x) совп. с поним-й плотностью вер-ти в т. 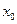. Что и требовалось доказать.

75. Показательный закон.

Случайная величина Х, принимающая только неотрицательные значения, распределена по показательному закону, если для некоторого параметра λ›0 функция плотности имеет вид:

f(x)= λe^-λx, x≥0

График функции плотности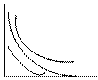

Функцию распределения найдем по формуле

F(x)=S^x₀f(x)dt

Подставляя выражение для функции плотности, получим

F(x)=S^x₀ λe^-λtdt=-e^-λt ₀ ¹=1- e^-λx, x≥0

 

 

 

76. Как определяется равномерный закон распределения на отрезке [ a, b ]? Укажите формулу для функции плотности f(x), найдите соответствующую функцию распределения F(x) и постройте графики функции f(x) F(x).

Скажем, что случайная величина X, сосредоточенная на отрезке [ a, b ], равномерно распределена на этом отрезке, если ее функция плотности равна константе:

Значение постоянной с определяется из условия:

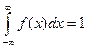
График f (x)

 

 

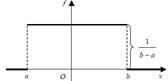
Связь между функцией распределения и плотностью вероятности дается форму-лой

Подставляя сюда функцию f (t), получим:

 

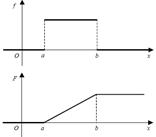
77. Возможно ли равномерное распределение на всей числовой оси? Чему равна вероятность Р(c<X<d) для равномерно распределенной на отрезке [a,b] случайной величины Х? Рассмотрите случаи: 1) c>a, d<b и 2) c<a, d<b.

1)Р(c<X<d)=

2) Р(c<X<d)=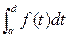

 

Непрерывная СВ Х имеет равномерный закон распределения на всей числовой оси, если ее плотность вероятности f (x) постоянна на всей числовой оси, т.е. f(x)=const.

 

78. Как определяется нормальный закон распределения на прямой? Укажите формулу для функции плотности f (x), найдите соответствующую функцию распределения F (x) и приведите формулу для вычисления вероятности P (α ≤ X ≤ β).

Мы говорим, что непрерывная случайная величина Х подчиняется нормальному закону распределения, если она имеет плотность вероятности следующего специального вида:

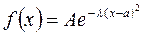, где

А, и а – постоянные, причем А>0, >0.

 

Стандартная запись функции плотности нормального закона распределения.

 

Найдем функцию распределения нормальной случайной величины.

Общая формула:

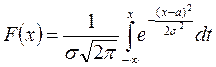
Заменим 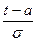на z. Получим 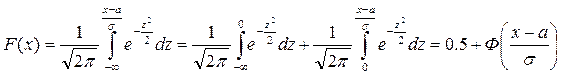, где

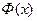есть функция Лапласа.

Таким образом, функция распределения нормальной случайной величины:

 

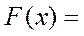
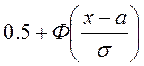
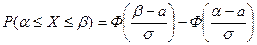
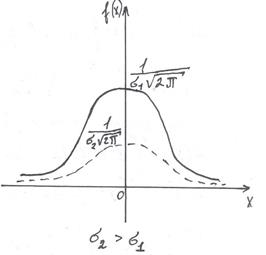
79. Запишите плотность распределения нормальной случайной величины x, для которой М(x)=m, D(x)=δ². Как изменится график плотности распределения, если: а) увеличится m, б) увеличится δ?

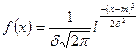
а) известно, что графики функций f(x) и f(x-a) имеют одинаковую форму: сдвинув график f(x) в положительном направлении оси x на а единиц масштаба при а<0 получим график f(x-a). Отсюда следует, что изменение величины параметра m (математического ожидания) не изменяет формы нормальной кривой, а приводит лишь к её сдвигу вдоль оси Ох. При увеличении m график плотности сдвинется вправо.

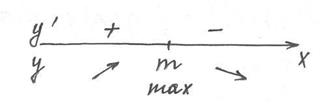
2) Исследуем функцию на экстремум.

f’(x)=0 при x=m

При x=m функция имеет максимум

С возрастанием δ максимальная ордината нормальной кривой убывает, а сама кривая становится более пологой, т.е. сжимается к оси Ох.

Как вычисляется математическое ожидание в случае распределения с плотностью f(x)? Может ли для какой-либо абсолютно непрерывной случайной величины не существовать математического ожидания? Ответ обоснуйте.

Математическое ожидание абсолютно непрерывной СВ Х с функцией плотности f(x) определяется равенством: М(Х)= интеграл xf(x)dx от минус беск до плюс беск

Мат. ожиданием случайной величины Е называется число 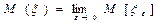. Если указанный справа предел не существует, то мат. ожидание величины х также считается несуществующим.

Если дискретная случайная величина Х принимает счетное множество возможных значений, то , причем мат. ожидание существует, если ряд в правой части равенства сходится абсолютно. Т.к. ряд может и расходиться, то соотв. случайная величина может и не иметь мат. ожидания. На практике, как правило, множество возможных значений случайной величины распространяется лишь на ограниченный участок оси абсцисс и, значит, мат. ожидание существует.

81. Как вычисляется дисперсия в случае распределения с плотностью f (x)? Докажите, что для случайной величины X с плотностью 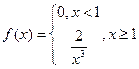дисперсия D (X) не существует, а математическое ожидание M (X) существует.

⇐ Предыдущая123456789Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: