Каков смысл начальных и центральных моментов двумерного случайного вектора (X,Y)?Ответ обоснуйте.

Первые начальные моменты – это математические ожидания случайных величин Х и У.

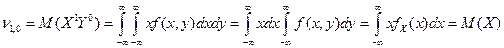, аналогично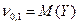

Точка с координатами (М(Х),М(У)) характеризует центр системы случайных величин, вокруг которого происходит рассеивание возможных значений. Кроме первых моментов широко используют вторые центральные моменты, которые бывают трех типов. Два из них дают знакомые нам дисперсии компонент Х и У:

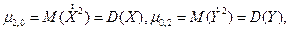которые характеризуют рассеивание возможных значений случайных величин X и 7 вдоль осей х и у.

Особую роль в определении взаимодействия компонент играет второй смешанный центральный момент

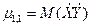
102.Дайте определение корреляционной и ковариационной матриц для системы случайных величин Х1,Х2…Хn и сформулируйте их основные свойства.

Для набора случайных величин X 1, X 2, …, Xn ковариационной матрицей и корреляцион-

ной матрицей называют квадратные матрицы порядка n, составленные из всех парных ко-

вариаций и всех коэффициентов корреляции

 

Пусть C – ковариационная матрица случайных величин – произвольный ненулевой вектор констант. Тогда для случайной величины

выполняется соотношение

при этом условие 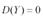равносильно равенству , означающему вырожденность матрицы C.

Ковариационная и корреляционная матрицы всегда симметричны и неотрицательно определены,

поэтому их определители неотрицательны:

Определитель корреляционной матрицы удовлетворяет также дополнительному ограничению:

103. Как найти ковариацию Сov(X,Y) случайных величин X и Y, если известна функция плотности

двумерного распределения (X;Y)? Верно ли, что из равенства Сov(X,Y)=0 вытекает независимость X и Y, если (X;Y) – двумерный нормальный случайный вектор?

Ковариацией или корреляционным момен­том случайного вектора (X, Y) называют величину

Cov(X, Y) =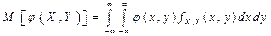

Ковариация обладает следующими свойствами:

1. Соv(Х, Y) = M(XY) - M(X)M(Y).

2. 3. 4. 5. 6. 7. 8.

Соу(Х, X) = D(X).

D(X+Y) = D(X) + D(Y) + 2Cov(X, Y).

Если X и Y независимы, то Cov(X, Y) = 0.

Cov(X, Y) = Cov(Y, X).

Cov(aX,Y) = Cov(X,aY) = aCov(X, Y).

Coy(X+Y, Z) = Cov(X, Z) +Coy(Y,Z).

Cov(X, Y+ Z) = Cov(X, Y) + Cov(X, Z).

 

Если Cov(X, Y) = 0, то случайные величины X и Y называются некоррелированными. Таким образом, согласно свойству 4 из неза­висимости X и Y следует их некоррелированность. Обратное ут­верждение неверно.

104. Укажите формулу для плотности распределения случайной величины Y +X= Z, если (X,Y) – двумерный случайный вектор с функцией плотности f(x,y) и независимыми компонентами X и Y. Приведите пример ее применения.

 

если даны 2 независ. случ. величины Х и У, распределённые равномерно соответственно на отр-ках [0,m] и [0,n] (m<=n), то можно найти функцию плотности Z=X+Y.

Z сосредоточена на отр-ке [0,m+n], формула принимает вид

 

При :

При

 

При

 

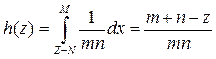
Как определяются условные законы распределения для дискретных случайных величин X и Y?

Мы можем найти зависимость СВ через условные законы распределения, т.е. закона распределения одной СВ, при условии, что др. СВ приняла определенное значение.

Если СВ X и Y дискретные, то их условные законы распр-я могут быть определены, используя теорию умножения вероятностей P(X= | Y= )= , для всех , таких что >0 определяет усл. распределение ДСВ x, при условии .

P(Y= | X= )= , для всех , таких что >0 опред. условие распр-е ДСВ y, при условии .

106 Сформулируйте определение условной ф-ии распр СВ Х при усл Y=y. Как определяется условная плотность f(y|x) распределения? Чему равна f(y|x), если СВ X и Y независимы?

Набор вероятностей f_x|y(x_k|y_k)=P(X=x_k|Y=y_l)={P(X=x_k,Y=y_l)}/P(Y=y_l) для всех y_l, таких, что P(Y=y_l)>0 определяет условное распределение дискретной СВ Х при условии Y=y_l. Аналогично для определения условного распр Y при условии X=x_k. Если X и Y независимы, то f_X|Y(x_k|y_y)=f_X(x_k); f_Y|X(y_l|x_k)=f_Y(y_l).

⇐ Предыдущая123456789

Поделиться:

Воспользуйтесь поиском по сайту: