Сформулируйте и докажите теорему сложения вер-тей для любых событий A и B. Что такое правило сложения вер-тей для несовместных соб. A и B?

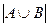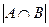Теорема слож. вер-тей. Для любых соб. A и B выполняется формула P(A+B)=P(A)+P(B)-P(AB)Док-во: Обозначим через n= - общее число исходов, ns- число исходов, благоприятных для соб. S.Тогда формулу = + – можно переписать след. образом nA+B=nA+nB-nAB(*).

Разделив почленно формулу (*) на n, получим формулу P(A+B)=P(A)+P(B)-P(AB)

Правило сложения вер-тей. Если соб. A и B несовместны, то P(A+B)=P(A)+P(B).Док-во:Т.е. соб. A и B несовместны, то P(AB)=0, поэтому из формулы P(A+B)=P(A)+P(B)-P(AB), получим P(A+B)=P(A)+P(B).

11 Какие соб.A1,A2,…An называются попарно несовместными? Сформулируйте правило сложения вер-тей для попарно несовместных соб. A1, A2, …An. Приведите пример попарно несовместных событий A,B, и C, таких что P(A+B+C)<1?

A1,A2,…An – попарно несовместны, если они никогда не выполняются одновременно. Исходя из следствия, можно сказать, что вер-ть появления одного из нескольких попарно несовместных соб., безразлично какого, равно сумме вер-тей этих соб. P(A1+A2+…+An)=P(A1)+P(A2)+…+P(An).Док-во: Рассмотрим 3 соб.A,B,C. Т.к. рассматриваемые события попарно несовместны, то появление одного из трех событий, A,B,C, равносильно наступлению одного из двух соб,A+B и C, поэтому в силу указанной теоремы

P(A+B+C)=P 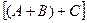=P(A+B)+P(C) =P(A)+P(B)+P(C).

Пример: Существуют 5 карточек с написанными цифрами: 1,2,3,4,5. è

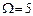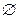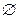. Соб.А – вытащили карточку с числами, делящимися на 2, В – делящ. на 3, С – делящ. на 5. События А,В,С попарно независимы. АВ= , АС= , ВС= 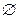. è P(A+B+C)=P(A)+P(B)+P(C).

, , èP(A+B+C)=0,4+0,2+0,2=0,8<1.

12 Объясните, почему Р(А+В)≤Р(А)+Р(В) для событий A и B. Чему равна сумма P(A)+P() вероятностей противоположных событий? Ответ обоснуйте.

А и В – как сов., так и несов. события.

Р(А+В)=Р(А)+Р(В) - Р(АВ)

 

Когда мы считаем P(А+В), то при сложении Р(А) и Р(В) мы дважды учитываем пересечение, то есть его надо вычесть:

Р(А)+Р(В)=Р(АВ)+Р(А`В)+Р(А+В)- Р(А`В)ÞР(А)+Р(В)=Р(АВ)+Р(А+В)

Р(А+В)=Р(А)+Р(В)-Р(АВ)

Р(А+В)≤Р(А)+Р(В)

Исходя из следствий (теорема сложения вероятностей) можно сказать, что сумма вероятностей противоположных событий равна единице. P(A)+P()=1. Т.к. события A и несовместны, поэтому можно применить формулу P(A+B)=P(A)+P(B). При этом следует использовать то, что событие A+ - достоверное, поэтому его вер-ть =1.Также используют такую формулу, выражающую вер-ть события A через вер-ть противоположного события . P(A)=1-P()

 

13 Верно ли, что если событие A является следствием события B,то P(A) ≤ P(B)? Ответ обоснуйте.

Да, верно, т.к. согласно следствию: если соб B явл. следствием соб. A, то P(A) ≤ P(B). Т.к. A B, то B=A+(B/A)- сумма несовместных событий. Применяя правило сложения вер-тей, имеем P(B)=P(A)+P(B/A), откуда следует неравенство P(A) ≤ P(B)

14. Дайте определение условной вероятности и приведите его статистическую интерпретацию. Укажите примеры, когда: 1) Р_B(А)>Р(А); 2) Р_B(А)<Р(А);

Пусть А и В случайные события по отношению к какому либо опыту причем P(B) неравно 0. число Р_B(А)=Р(АВ)/Р(В) называют вероятностью события А при условии что событие В уже наступило или просто условной вероятностью А. Наличие условной вероятности (Р_B(А)≠Р(А)) между событиями определяет их взаимосвязь.

Статистическая интерпретация: Рассмотрим некий эксперимент и 2 соб. А и В. Повторим опыт к раз. Пусть - число опытов, в которых произойдет событие А при условии что В тоже произойдет.

1) Р_B(А)>Р(А) бросаем кость, В- выпало четное, А-выпала двойка. Р(А)=1/6 Р_B(А)=1/3

2) Р_B(А)<Р(А) в коробке лежит 3 белых и 3 черных шара вытащили 1 шар, А – вытащить черный шар, В- из коробки предварительно вынули шар оказавшийся черным.

Р(А)=1/2 Р_B(А)=2/5

Какие события называются независимыми? Докажите, что если события

A и B независимы, то независимы события A и B

Если выполняется равенство Р_B(А)=Р(А) то события А и В независимы. Для двух независимых событий А и В имеем Р(АВ)=Р(А)*Р(В)- правило умножения вероятностей для двух событий.

А=АВ+АВ Þ Р(А)= Р(АВ)+Р(АВ), или Р(А)=Р(АВ)+Р(А)Р(В). Отсюда Р(АВ)=Р(А)[1-Р(В)], или Р(АВ)=Р(А)Р(В)

 

⇐ Предыдущая123456789Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: