 |
Сформулируйте и докажите формулу Байеса. Приведите пример ее применения.
|
|
|
|
Пусть событие А может наступить при условии появления одного из несовместных событий В1,В2,…,Вn, образующих полную группу. Поскольку заранее неизвестно, какое из этих событий наступит, их называют гипотезами. Вероятность появления события А определяется по формуле полной вероятности:
Р(А) = Р(В1) Рв1(А) + Р(В2)Рв2 (А) + ….+ Р(Вn) Рвn (А) (1)
Допустим, что произведено испытание, в результате которого появилось событие А. Определим, как изменились, в связи с тем, что событие А уже наступило, вероятности гипотез. Другими словами, будем искать условные вероятности
Ра(В1), Ра(В2),…., Ра(Вn).
Найдем вначале условную вероятность Ра(В1). По теореме умножения имеем
Р(АВ1) = Р(А) Ра(В1) = Р(В1)Рв1(А)
Отсюда
Ра(В1) = Р(В1)Рв1(А)
Р(А)
Заменим здесь Р(А) по формуле (1), получаем
pA(Hi)= рвi(A)p(Вi).
рВ1(А1)р(В1)+рВ2(А)р(В2)+…+рВn(А)р(Вn)
Аналогично выводятся формулы, определяющие условные вероятности остальных гипотез, т.е. условная вероятность любой гипотезы Вi (i= 1,2,…,n) может быть вычислена по формуле
Ра(Вi) = Р(Вi) Рвi(А)
Р(В1) Рв1(А) + Р(В2) Рв2(А)+….+Р(Вn) Рвn(А)
Полученные формулы называются формулы Байеса. Они позволяют переоценить вероятности гипотез после того, как становится известным результат испытания, в итоге которого появилось событие А.
Пример:
Имеется три одинаковых по виду ящика. В первом ящике n=12 белых шаров, во втором – m=4 белых и n-m=8 черных шаров, в третьем – n=12 черных шаров. Из выбранного наугад ящика вынули белый шар. Найдите вероятность Р того, что шар вынут из второго ящика.
Решение. 
30. В чем состоит схема Бернулли? Запишите формулу 
для вероятности k успехов в серии n испытаний по схеме Бернулли и приведите пример ее применения.
Схема Бернулли: производится n независимых испытаний, в каждом из которых с одной и той же вероятностью p наступает некоторое событие А (называемое обычно «успехом») и, следовательно, с вероятностью q=1-p наступает событие 
, противоположное А.
|
|
|
Пусть k – любое из чисел 0,1,2,…, n. Обозначим 
вероятность того, что в n испытаниях Бернулли успехов наступит k раз. Справедлива формула Бернулли:
.
Пример: Монета бросается 10 раз. Какова вероятность того, что герб выпадает при этом ровно 3 раза?
Решение: В данном случае успехом считается выпадение герба, вероятность p этого события в каждом опыте равна ½, так что q=1-p=1|2. Отсюда
.
31. Выведите формулу для вероятности k успехов в серии n испытаний по схеме Бернулли.
Когда производится n одинаковых и независимых опытов, каждый из которых имеет только 2 исхода { A; }. Т.е. некоторый опыт повторяется n раз, причем в каждом опыте некоторое событие А может появиться с вероятностью P(A)=q или не появиться с вероятностью P()=q-1=p.
Пространство элементарных событий каждой серии испытаний содержит 
точек или последовательностей из символов А и . Такое вероятностное пространство и носит название схема Бернулли. Задача же заключается в том, чтобы для данного k найти вероятность того, что при n- кратном повторении опыта событие А наступит k раз.
Для большей наглядности условимся каждое наступление события А рассматривать как успех, ненаступление А – как неуспех. Наша цель – найти вероятность того, что из n опытов ровно k окажутся успешными; обозначим это событие временно через B.
Событие В представляется в виде суммы ряда событий – вариантов события В. Чтобы фиксировать определенный вариант, нужно указать номера тех опытов, которые оканчиваются успехом. Например, один из возможных вариантов есть
. Число всех вариантов равно, очевидно, 
, а вероятность каждого варианта ввиду независимости опытов равна 
. Отсюда вероятность события В равна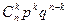 
. Чтобы подчеркнуть зависимость полученного выражения от n и k, обозначим его . Итак,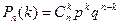 
.
|
|
|
|
|
|
