 |
Пример. Теоретические положения
|
|
|
|
Пример
Построение временных (переходных, весовых (импульсных переходных)) и частотных характеристик типовых звеньев автоматического управления на примере инерционного звена с передаточной функцией
.
В окне Simulink Library Browser необходимо выбрать исследуемое звено ( блок Transfer Fcn ) и, удерживая левую кнопку мыши, перетащить этот блок в окно модели.
Переходная характеристика звена представляет собой реакцию звена на единичную ступенчатую функцию.
Весовая (импульсная переходная) характеристика звена представляет собой реакцию на d - функцию Дирака и равна производной по времени от переходной характеристики.
Для получения переходной характеристики звена на его вход подается ступенчатое воздействие ( блок Step ). Весовую характеристику можно получить дифференцируя ( блок Derivative ) переходную характеристику исследуемого звена (рис. 1. 15), т. е. включая на выходе звена дифференциальное звено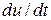 
.
Аналогично, как и инерционное звено, располагаем блок Step в рабочей области. Затем следует провести линии связи, для этого указатель мыши помещается на выходной порт блока Step, который обозначается угловой скобкой «> » на правой стороне изображения блока. При этом указатель примет вид креста. Далее, при нажатой левой кнопке мыши, указатель мыши перемещается ко входному порту другого блока, он обозначается угловой скобкой «> », расположенной на левой стороне изображения блока. В случае верно выбранной точки входа указатель принимает вид двойного креста. Аналогичным образом к схеме подключается звено .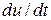
Теперь нам необходимо задать параметры блоков. Двойным нажатием левой кнопки мыши на соответствующем блоке, появляется диалоговое окно Block Parameters. Для блока Step мы вводим в области step time диалогового окна Block Parameters: step ноль. Для блока Transfer Fcn мы вводим в области numerator диалогового окна Block Parameters: Trabsfer Fcn – [10], а в области denominator – [0. 1 1].
|
|
|
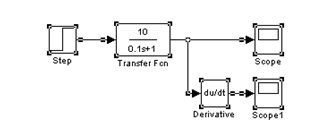
Рис. 1. 11. Схема для получения весовой и переходной функции инерционного звена
Для построения графических зависимостей нам необходимо подключить еще один блок ( блок Scope или блок XY Graph ).
Рис. 1. 12. Схема для построения частотных характеристик инерционного звена
Далее нам необходимо задать параметры эксперимента. Выбираем команду Simulation parameters меню Simulation окна модели и в группе опций Simulation time диалогового окна Simulation parameters в текстовых полях Start time и Stop time задается время моделирования. В группе опций Solver options в текстовом поле type задается шаг интегрирования: переменный ( Variable step ) или постоянный ( Fixed step ), метод интегрирования и значение шага интегрирования. Затем выбирается команда Start меню Simulation и строятся графики.
Для снятия частотной характеристики звена необходимо на вход подавать синусоидальные сигналы ( блок Sin Wave ) с различными частотами.
В диалоговом окне Block Parameters: Sin Wave задаются значения амплитуды, частоты и фазы.
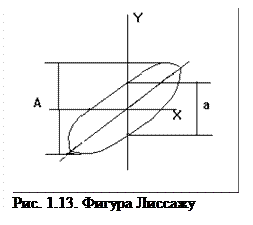Значение амплитудной частотной характеристики на заданной частоте определяется как отношение амплитуд сигналов на выходе и входе звена, а значение фазочастотной характеристики можно определить по фигуре Лиссажу, выводимой на экран с помощью блока XY Graph и подаче на один вход входного, а на другой- выходного сигнала звена. Фаза (угол j ) определяется по формуле 
Часто задачей исследования является рассмотрение процессов, происходящих в замкнутых автоматических системах. Для этого необходимо в схему добавить сумматор, на один вход которого будет действовать входной сигнал, а на второй следует завести обратную связь. Если обратная связь отрицательная, то это необходимо учесть или при задании параметров сумматора (соответствующий параметр должен быть равен -1), или включением в цепь обратной связи блока-инвертора.
|
|
|
Теоретические положения
Для описания линейных непрерывных систем автоматического управления (САУ) широко используются временные и частотные характеристики, основным преимуществом которых является то, что они могут быть экспериментально получены при исследовании системы. В качестве временных характеристик наиболее часто используются переходные и весовые (импульсные переходные) функции, представляющие собой реакции САУ на единичную ступенчатую функцию и δ -функцию Дирака соответственно. Схема снятия частотных характеристик объекта представлена на рис. 1. 14.
Рис. 1. 14. Схема снятия частотных характеристик объекта
Период колебаний равен T1 =2π /ω , а сдвиг по времени ∆ t = φ /ω
Используя формулу Эйлера: 
, входной и выходной сигналы объекта можно представить в виде:
x(t) = A вхsin wt = Im{Aвх ejwt }=Im{ 
}
y(t) = A вых sin (wt + j)=Im{Aвыхej(wt+j)}=Im{ 
}.,
где Im – выделение мнимой части комплексного числа,
- входной сигнал в комплексной форме,
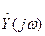- выходной сигнал, представленный в комплексной форме
Основой всех частотных характеристик является комплексный коэффициент усиления, определяемый выражением
.
На основании выражения для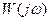 
можно определить амплитудно-фазовую АФХ W(j ω ), амплитудную А(ω ) и фазовую φ (ω ) частотные характеристики, а также логарифмические амплитудную L( ω )=20LgA( ω ) (ЛАЧХ) и фазовую φ (ω ) (ЛФЧХ) частотные характеристики (при изменении частоты ω от 0 до ∞ ).
|
|
|
