 |
Подготовка к работе. Задание на выполнение работы. Методические указания. Контрольные вопросы. Литература. Лабораторная работа № 2
|
|
|
|
Подготовка к работе
Согласно номеру бригады для 2-х звеньев с указанными в табл. № 1. 2 параметрами, записать передаточные функции и построить:
• логарифмическую амплитудно-частотную характеристику (ЛАЧХ);
• логарифмическую фазочастотную характеристику (ЛФЧХ);
• амплитудно-фазовую характеристику (АФХ);
• весовую и переходную функции (можно в Mathcad).
Изучить возможности и назначение ПК " SIMULINK".
Задание на выполнение работы
1. С помощью ПК " SIMULINK" построить для 2-х звеньев (тип исследуемых звеньев и их параметры указаны в таблице 1. 2, а обозначения и передаточные функции приведены ниже):
а) интегрирующего W(p) = k/p;
б) инерционного W(p) = k/(l+T1p);
в) упругого дифференцирующего W(p) = k(l+T2p)/(l+T1p), T2 > T1
г) упругого интегрирующего W(p) = k(l+T2p)/(l+T1p), T2 < T1;
д) колебательного W(p) = k/(1+2ξ T1p+T12p2)
е) реального дифференцирующего W(p) = kp/(l+T1p).
• переходную характеристику;
• весовую характеристику.
По полученным зависимостям определить параметры звеньев.
2. Для исследуемых звеньев снять амплитудно-частотные и фазочастотные характеристики.
3. По снятым данным построить ЛАЧХ, ЛФЧХ и АФХ, сравнить их с построенными при подготовке к работе и определить по ним параметры звеньев.
Методические указания
Для снятия временных характеристик использовать схему моделирования с помощью программного комплекса “SIMULINK”, представленную на рис. 1. 11, в которой следует использовать блоки, моделирующие исследуемые в работе типовые звенья. Снятие частотных характеристик производится с использованием синусоидального сигнала различной частоты рис. 1. 12. При снятии частотных характеристик следует выбирать шаги интегрирования и выдачи данных такими, чтобы на периоде синусоиды T1 было не меньше 10 точек. Время выдачи должно выбираться из условия окончания переходного процесса в исследуемом типовом звене, диапазон изменения частот выбирается по построенной при подготовке к работе логарифмическим частотным характеристикам..
|
|
|
Таблица 1. 2
| № брига-ды | Вариант Тип звена | Коэффи-циент К | Постоян-ная времени Т1 | Постоян-ная времени Т2 | Декремент затухания ξ |
| а, г | 1. 0 | 5. 0 | 2. 0 | - | |
| а, д | 2. 0 | 3. 0 | - | 0. 5 | |
| в, г | 3. 0 | 2. 0 | 5. 0 | - | |
| б, д | 4. 0 | 5. 0 | - | 0. 6 | |
| б, в | 5. 0 | 2. 0 | 4. 0 | - | |
| б, г | 6. 0 | 3. 0 | 1. 0 | - | |
| в, д | 7. 0 | 1. 0 | 3. 5 | 0. 25 | |
| г, д | 8. 0 | 6. 0 | 2. 0 | 0. 15 | |
| б, е | 9. 0 | 1. 5 | - | - | |
| е, д | 10. 0 | 3. 5 | - | 0. 55 | |
| а, б | 5. 0 | 3. 0 | - | - | |
| а, в | 7. 5 | 2. 0 | 10. 0 | - | |
| а, е | 4. 0 | 2. 5 | - | - | |
| в, е | 5. 0 | 1. 0 | 5. 0 | - | |
| г, е | 2. 5 | 5. 0 | 2. 0 | - |
Контрольные вопросы.
1. Что такое весовая и переходная функции объекта (системы), какие сигналы надо подавать на вход системы для их получения, какова связь между этими временными характеристиками.
2. Какие сигналы надо подавать на вход системы (объекта) для получения частотных характеристик.
3. Как снимаются амплитудные и фазовые характеристики систем.
4. Какова связь между передаточной функцией системы и ее комплексным коэффициентом усиления.
5. Записать дифференциальные уравнения, описывающие типовые динамические звенья (а – е).
Литература
. 1. Теория автоматического управления. Ч. I, II. Под ред. Нетушила А. В., М.: Высш. школа, 1982, 400 c.
2. Петрова В. А., Ягодкина Т. В. Математическое описание линейных непрерывных САУ. М.: Изд. МЭИ, 1992, 103 c.
3. Дьяконов В. П. MATLAB 6/6. 1/6. 5 + Simulink 4/5. Основы приме-нения. М.: СОЛОН-Пресс, 2004.
|
|
|
ЛАБОРАТОРНАЯ РАБОТА № 2
Исследование качества систем автоматического управления
Цель работы: изучение временных характеристик систем автоматического управления (САУ) и определение основных показателей качества переходного процесса.
Теоретические положения
Основное условие работоспособности систем автоматического управления заключается в ее устойчивости. Однако устойчивость -недостаточное условие ее практического применения. Наряду с этим выдвигаются определенные требования к качеству процессов регулирования. Комплекс требований, определяющих поведение системы в установившемся и переходном режимах отработки заданного воздействия определяется показателями качества работы САУ: прямыми показателями качества (быстродействием и характером переходного процесса), определяемыми по переходной характеристике САУ, косвенными (запасами устойчивости по амплитуде и фазе), точностью.
Показатели качества процесса отработки входного воздействия будем рассматривать для системы, структурная схема которой изображена на рис. 2. 1.
Рис. 2. 1. Структурная схема САУ
Запасы устойчивости по амплитуде и фазе
Линейная система устойчива, если с течением времени переходная составляющая процесса стремится к нулю:
xпер. (t) = 0, xпер. (t) = 
, где сi – постоянные интегрирования,
pi – корни характеристического уравнения исследуемой САУ.
Уравнение динамики системы (рис. 2. 1) в изображении по Лапласу имеет вид
[1+Wp(p)]·Y(p) = Wp(p)·Xy(p)±WII(p)·Xв(p),
где Wp(p) = WI(p)· WII(p) = K(p)/D(p) – передаточная функция разомкнутой системы. Уравнение свободного режима [1+Wp(p)]·Y(p) = 0.
Характеристическое уравнение замкнутой САУ:
A(p) = K(p)+D(p) = 0.
Для устойчивости линейной замкнутой САУ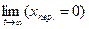 
необходимо и достаточно, чтобы вещественные части корней характеристического уравнения были отрицательными, т. е. лежали в левой части комплексной плоскости.
Замкнутая система должна быть не просто устойчивой, а обладать определенными запасами устойчивости по амплитуде и по фазе. Запас устойчивости по амплитуде определяется либо величиной
Δ A = 1-Aπ , либо величиной 1/ Aπ
|
|
|
(в логарифмических единицах Lπ = 20·lg(1/Aπ )[дБ]), где Aπ - значение модулявектора Wp(jω ), аргумент которого равен φ = -π (рис. 2. 2).
Рис. 2. 2. Определение запаса устойчивости по фазе γ
и модулю Δ A (1/Аπ )
Запас устойчивости по фазе обозначается γ и определяется на частоте среза ω с, при которой амплитуда A(ω с) = 1,
γ = 1800+φ (ω с), (2. 1)
где φ (ω с) - значение аргумента вектора Wp(jω ) при ω = ω с.
Изображенные на рис. 2. 2 и 2. 3 годограф Wp(jω ) и логарифмические характеристики разомкнутой системы показывают, что система в замкнутом состоянии устойчива и обладает запасом устойчивости по фазе γ > 0 и по амплитуде
Lπ = 20·lg(1/Aπ ) > 0 (1/Aπ > 1).
Рис. 2. 3. Определение запаса устойчивости по ЛАЧХ и ЛФЧХ
Коэффициент усиления, при котором замкнутая САУ находится на границе колебательной устойчивости называется предельным Кпред.
На основании критерия устойчивости Найквиста предельный коэффициент усиления может быть определен соотношением
Кпред = К·(1/Aπ ).
Предельный коэффициент усиления САУ можно определить по логарифмическим частотным характеристикам (рис. 2. 3. )
20·lgКпред = 20·lgK – 20·lg Aπ .
Если коэффициент усиления разомкнутой системы меньше предельного коэффициента Кпред, то система устойчива и обладает запасом устойчивости (по фазе, модулю). В противном случае - система неустойчива.
|
|
|
