Определение порядка реакции по периоду полупревращения

 

В методе определения порядка реакции по периоду полупревращения используют различный характер зависимости t _1/2 от начальной концентрации реагента. Для реакций нулевого порядка t _1/2 прямо пропорционально начальной концентрации реагента (уравнение (260)), для реакций первого порядка не зависит от начальной концентрации реагирующего вещества (уравнение (265)), для реакций второго порядка – обратно пропорционально начальной концентрации (уравнение (269)).

Реакция 0-го порядка		Реакция 1-го порядка		Реакция 2-го порядка
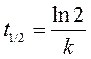
с 0, М	t 1/2, с		с 0, М	t 1/2, с		с 0, М	t 1/2, с
0,1	35,2		0,05	14,5		0,2
0,2	70,0		0,15	14,6		0,4
0,4			0,25	14,3		0,6

Для определения порядка изучаемой реакции необходимо экспериментально определить время полупревращения для нескольких начальных концентраций реагентов и установить, какая зависимость существует между ними. Для этого вначале анализируют экспериментальные данные в таблице, а затем, если зависимость между временем полупревращения и начальной концентрацией есть, строят в соответствующих координатах график, подтверждающий вид этой зависимости.

Значение константы скорости реакции находят по наклону прямой в соответствующих координатах используя или уравнение (260) (кинетика 0-го порядка), или (269) (кинетика 2-го порядка) или усреднением значений t _1/2 и расчетом константы по уравнению (265), если исследуемая реакция подчиняется кинетике 1-го порядка.

 

Дифференциальные методы

Метод Вант-Гоффа

Дифференциальный метод, предложенный Вант-Гоффом, заключается в следующем. Пусть изучается кинетика химической реакции

n _AА + n _BB ® … (270)

Если начальная концентрация реагента В значительно больше начальной концентрации реагента А, то концентрация В в процессе протекания реакции изменяется незначительно и может быть принята постоянной (метод избытка реагента). Тогда кинетическое уравнение:

(271)

упрощается

,

(272)

где .

Логарифмирование последнего уравнения приводит к линеаризованному уравнению:

.

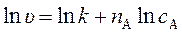(273)

Определяя в опытах скорость реакции при различных начальных концентрациях реагирующих веществ и строя график зависимости логарифма скорости реакции от логарифма концентрации, определяют коэффициент наклона полученной прямой, который будет равен порядку реакции по веществу, концентрация которого изменялась. Значение ln u при ln c _A = 0 равно ln k. Отсюда находят константу скорости химической реакции k в уравнении (272).

Этот метод можно применять в двух вариантах. В первом варианте определяют скорость реакции как производную dc / dt при разных начальных концентрациях. Проводят касательные к кривым в момент начала реакции.

Во втором варианте проводят только один опыт. Обработка кинетической кривой заключается в расчете наклонов касательных к кривой в различные моменты времени, соответствующие различным значениям концентраций реагентов.

Результаты, полученные в том и другом варианте, используются для построения зависимости логарифма скорости от концентрации реагента.

 

Примеры решения задач

1. Определить методом подстановки порядок и константу скорости реакции A ® … по зависимости концентрации реагента от времени, прошедшего с момента начала реакции. Температура 298 К.

№	t, c	c A, М		№	t, c	c A, М
		0,180				0,0346
		0,128				0,0249
		0,0929				0,0177
		0,0681				0,0129
		0,0474				0,0092

 

Решение:

Рассчитаем константу скорости изучаемой реакции в предположении, что это реакция 0-го, 1-го и 2-го порядка по уравнениям (259), (264) и (268). Анализ рассчитанных значений констант показывает, что постоянные значения константы получаются при выборе уравнения (264) для реакции 1 порядка. Из графика видно, что ее значения случайно колеблются около некоторого среднего значения. Следовательно, исследуемая реакция имеет 1-й порядок по веществу А. Среднее значение константы скорости равно 0,00331 с^–1.

№	t, c	c A, М	Константа для реакции
0 порядка	1 порядка	2 порядка
		0,180	–	–	–
		0,128	0,000520	0,00341	0,0226
		0,0929	0,000436	0,00331	0,0260
		0,0681	0,000373	0,00324	0,0304
		0,0474	0,000332	0,00334	0,0389
		0,0346	0,000291	0,00330	0,0467
		0,0249	0,000259	0,00330	0,0577
		0,0177	0,000232	0,00331	0,0728
		0,0129	0,000209	0,00330	0,0900
		0,0092	0,000190	0,00330	0,1146
Среднее значение константы, с–1		0,00331

2. Определить графическим методом порядок и константу скорости реакции A ® … по зависимости концентрации реагента от времени, прошедшего с момента начала реакции. Температура 298 К.

№	t, c	c A, М		№	t, c	c A, М
		0,180				0,0273
		0,0907				0,0241
		0,0590				0,0206
		0,0408				0,0193
		0,0328				0,0162

Решение:

Для определения порядка реакции этим методом рассчитаем по экспериментальным данным значения ln с, 1/ с и построим графики зависимостей " с – t ", "ln с – t ", "1/ с – t ", в которых линеаризуются кинетические уравнения (258), (262) и (267) реакций 0-го, 1-го и 2-го порядков соответственно.

№	t, c	c A, М	ln [ с, М]	1/ с, М–1
		0,180	–1,715	5,56
		0,0907	–2,400	11,0
		0,0590	–2,830	16,9
		0,0408	–3,199	24,5
		0,0328	–3,417	30,5
		0,0273	–3,601	36,6
		0,0241	–3,726	41,5
		0,0206	–3,882	48,5
		0,0193	–3,948	51,8
		0,0162	–4,123	61,7

 

Зависимость для изучаемой реакции является прямолинейной, если использовать уравнение (267), выведенное для кинетики 2-го порядка. Следовательно, изучаемая реакция является реакцией второго порядка по реагенту А.

 

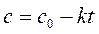
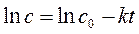
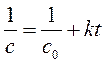
Константа скорости реакции в соответствии с уравнением (267) равна коэффициенту наклона 6,10×10^–2 л/(моль×с) в уравнении прямой, которое найдено методом наименьших квадратов.

3. Определить порядок и константу скорости реакции A ® … по времени полупревращения, используя экспериментальные данные, полученные при 298 К

 

с 0А, М	t 1/2, с
0,0317	26,9
0,0528	44,8
0,0916	81,5
0,134
0,294
0,403

Решение:

Анализ экспериментальной зависимости времени полупревращения от начальной концентрации реагента А (таблица) позволяет из уравнений (260), (265) и (269)

, , ,

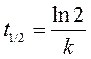сразу отбросить второе (так как в соответствии с этим уравнением время полупревращения должно быть постоянным, а, судя по таблице, оно не постоянно) и третье уравнение (так как в соответствии с этим уравнением время полупревращения должно уменьшаться с увеличением начальной концентрации реагента, а оно увеличивается).

Остается первое уравнение, выведенное для кинетики 0-го порядка, однако необходимо проверить, действительно ли время полупревращения реагента А, найденное в эксперименте, прямо пропорционально начальной концентрации реагента. Для этого построим график зависимости в координатах " t _1/2 – c ₀". Если в этих координатах зависимость будет иметь вид прямой, проходящей через начало координат, как и график уравнения (260), то это будет являться подтверждением того, что исследуемая реакция является реакцией 0-го порядка.

 

Прямолинейность графика и малая величина отрезка, отсекаемого на оси ординат при t _1/2 = 0 (2,3), подтверждают вывод о том, что исследуемая реакция имеет 0-ой порядок по реагенту А.

Константу скорости реакции находят из уравнения (260), которое, если выделить коэффициент перед начальной концентрацией, примет вид:

.

Расчет коэффициентов прямой (t _1/2 = 848,1 с ₀ + 2,3), выполненный по методу наименьших квадратов, приводит к ненулевому значению ординаты при с ₀ = 0 (t _1/2 = 2,3). Этим отличием от нуля, которое возникает из-за ошибок, допущенных в эксперименте в определении времени и концентраций, в нашем случае можно пренебречь, так как ошибка в определении этого коэффициента прямой больше самого значения коэффициента (подробности расчета здесь не приводим).

Таким образом

и значение константы скорости равно

.

4. Монохлоруксусная кислота при температуре 298 К гидролизуется (вода в большом избытке)

CH₂ClCOOH + H₂O ® CH₂OHCOOH + HCl

Были проведены четыре эксперимента, в которых измерялась концентрация монохлоруксусной кислоты от времени (начальная концентрация кислоты была различна)

 

t, мин
c 1, М	0,129	0,119	0,101	0,0925
c 2, М	0,0867	0,0787	0,0669	0,0616
c 3, М	0,0508	0,0466	0,0396	0,0363
c 4, М	0,0259	0,0237	0,0200	0,0186

 

Методом Вант-Гоффа определить порядок реакции и рассчитать кажущуюся константу скорости реакции.

 

Решение:

Так как вода взята в большом избытке, то можно применить метод Вант-Гоффа. Скорость реакцииравна (А – монохлоруксусная кислота)

По первым двум колонкам таблицы рассчитаем значения средних скоростей реакции (уравнение (252)) и соответствующие им средние значения концентраций (уравнение (253)), а также их натуральные логарифмы (в точных расчетах используют средние значения концентраций по времени; в ориентировочных эту величину можно заменить средней по концентрации).

c сред	u сред	ln c сред	ln u сред
0,124	0,0000500	–2,087	–9,903
0,0827	0,0000400	–2,493	–10,127
0,0487	0,0000210	–3,022	–10,771
0,0248	0,0000110	–3,697	–11,418

Для нахождения порядка и константы скорости реакции по коэффициентам уравнения (273) строим график в координатах "ln u – ln c _A".

Угловой коэффициент уравнения рассчитанный по графику (рисунок) близок к 1; из этого следует, что порядок реакции по монохлоруксусной кислоте близок к 1, а кажущаяся константа скорости в уравнении (272) равна

 

⇐ Предыдущая26272829303132333435Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: