 |
Задачи для самостоятельного решения.
|
|
|
|
1. Вычислить на сколько градусов необходимо повысить температуру, чтобы скорость реакции возросла в 50,0 и в 100 раз, если температурный коэффициент скорости реакции равен 3,00.
(Ответ: на 35,6 К; на 41,92 К)
2. Термическое разложение этиленоксида является реакцией 1-го порядка. При 378,5°С период полупревращения этиленоксида равен 363 мин. Определить константу скорости реакции при 450°С. Энергия активации данной реакции 217 кДж/моль.
(Ответ: 0,1 мин–1)
3. Константа скорости омыления этилацетата гидроксидом натрия при 9,4°С равна 2,37 л/(моль×с), а при 14,4°С – 3,20 л/(моль×с). Рассчитать температурный коэффициент скорости реакции в указанном интервале температур и энергию активации.
(Ответ: 1,823; 40,5 кДж/моль)
4. Гидролиз 1-метил-1-хлорциклогексана в 80% этаноле протекает по реакции 1-го порядка. Экспериментально получены следующие константы скорости
| T, К | 273,0 | 298,0 | 308,0 | 318,0 |
| k, с–1 | 1,06×10–5 | 3,19×10–4 | 9,86×10–4 | 2,92×10–3 |
Вычислить энергию активации графическим методом.
(Ответ: 90,0 кДж/моль)
5. Для ускоренного определения срока годности лекарственного препарата были проведены эксперименты при повышенной температуре 40°С. В предварительных экспериментах было обнаружено, что реакция разложения лекарственного вещества подчиняется кинетике 1-го порядка. Энергия активации равна 55,2 кДж/моль. Обнаружено, что срок годности при этой температуре (время за которое разлагается 10% исходного вещества) равен 164 сут. Рассчитать срок годности при хранении лекарственного препарата при температуре 25°С и тех же прочих условиях.
(Ответ: 477 сут)
Сложные реакции
При изучении кинетики сложных реакций, включающих несколько элементарных стадий, используют принцип независимости химических реакций:
|
|
|
Ø если в системе протекает несколько простых реакций, то каждая из них подчиняется основному постулату химической кинетики и протекает независимо от других реакций.
Основные типы сложных реакций рассмотрим на примере реакций первого порядка.
Обратимые реакции
А В
Эта схема описывает реакции изомеризации в газовой фазе или в растворе, например: бутан изобутан, цис -стильбен транс- стильбен.
Основываясь на законе действующих масс и принципе независимости, получаем следующее уравнение:
 . .
| (280) |
Если начальные концентрации веществ А и В обозначить соответственно a и b и ввести степень превращения х (с А = a – x, с В = b + x), то кинетическое уравнение приобретает вид:
 . .
| (281) |
Решение уравнения (282) можно выразить через степень превращения х ¥, соответствующую достижению равновесия:
 , ,
| (282) |
где х ∞ – предельное значение степени превращения, которое можно рассчитать по уравнению (283) при достижении состояния равновесия:
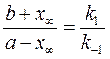 , ,
| (283) |
откуда следует:
 . .
| (284) |
Состояние равновесия в этой реакции характеризуется константой равновесия:
 . .
| (285) |
Кинетические кривые для обратимых реакций первого порядка приведены на рисунках 56 и 57.

Рис. 56. Зависимость концентраций реагента и продукта от времени для обратимой реакции первого порядка при K >1

Рис. 57. Зависимость концентраций реагента и продукта от времени для обратимой реакции первого порядка при K <1
Параллельные реакции

Примерами таких реакций являются нитрование фенола с образованием о -, м - и п - нитрофенола, нитрование смеси бензола и толуола. Кинетическое уравнение записывается с учетом принципа независимости:
 , ,
| (286) |
а его решением является уравнение:
 . .
| (287) |
Для параллельных реакций в любой момент времени отношение концентраций продуктов постоянно и определяется константами скорости элементарных стадий:
|
|
|
 . .
| (288) |
Кинетические кривые для случая двух параллельных реакций первого порядка приведены на рисунке 58.

Рис. 58. Зависимость концентраций реагента и продуктов от времени для параллельных реакций первого порядка, k 1> k 2
3. Последовательные реакции

К таким реакциям относятся, например, такие важные химические процессы, как полимеризация, термический крекинг углеводородов, хлорирование углеводородов.
Кинетические кривые для случая двух последовательных реакций первого порядка приведены на рисунке 59. Кривая, показывающая изменение концентрации вещества А, имеет вид экспоненты. Анализируя кривые изменения концентраций веществ В и D, можно увидеть, что в начале и в конце реакции вещества В нет в системе, поэтому кривая проходит через максимум.
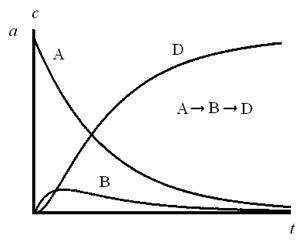
Рис. 59. Зависимость концентраций веществ от времени в реакционной смеси, в которой протекают две последовательные реакции первого порядка, k 1/ k 2 = 0,2
Примеры решения задач
1. Для обратимой реакции первого порядка
А В
константа равновесия K = 8, а k 1 = 0,4 с–1. Вычислите время, при котором концентрации веществ А и В станут равными, если начальная концентрация вещества В равна 0.
Решение:
Из константы равновесия (285) находим константу скорости обратной реакции:

По условию задачи необходимо найти время, за которое прореагирует ровно половина вещества А (уравнение (283)):

Подставив вместо х ∞ его выражение (уравнение (284)) и заменив х = а /2 в решении кинетического уравнения для обратимых реакций (283), получим следующее выражение:
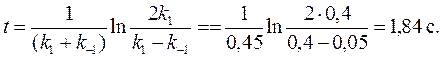
2. В параллельных реакциях первого порядка

выход вещества В равен 63%, а время превращения А на 1/3 равно 7 минут. Найдите k 1 и k 2.
Решение:
Кинетическое уравнение (286) для превращения вещества в параллельных реакциях имеет вид уравнения первого порядка, в которое вместо одной константы скорости входит сумма констант скоростей отдельных стадий. Следовательно, по аналогии с реакциями первого порядка, по времени превращения А на 1/3 можно определить сумму констант k 1+ k 2 по уравнению (287):

Выход вещества В равен 63%, а вещества D – 37%. Отношение этих выходов равно отношению конечных концентраций веществ В и D, следовательно оно равно отношению соответствующих констант скорости:
|
|
|

Решая это уравнение совместно с предыдущим, находим:
k 1 = 0,037 мин–1, k 2 = 0,021 мин–1.
|
|
|


