 |
3. 3. Оценка точности функции измеренных величин
|
|
|
|
Решение
Результаты расчетов сведены в таблицу 3. 1 (табличная форма).
Табл. 3. 1
| № п/п | Результаты измерений
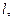 м м
| Погрешности измерений
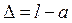 , см , см
| 
|
| 217, 24 | +0, 4 | 0, 2 | |
| 217, 31 | +7, 4 | 54, 8 | |
| 217, 28 | +4, 4 | 19, 4 | |
| 217, 23 | -0, 6 | 0, 4 | |
| 217, 20 | -3, 6 | 13, 0 |
 = 87, 8
= 87, 8
СКП равна
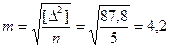 см.
см.
СКП самой СКП
 см.
см.
Следовательно,
 см.
см.
Предельная погрешность равна
 .
.
Погрешности всех пяти измерений меньше предельной погрешности, следовательно, нет оснований предполагать, что измерения имеют грубые погрешности.
Пример 2
Площадь теодолитного полигона была измерена 8 раз планиметром (см. табл. 3. 2). Та же площадь была вычислена аналитическим методом и получен результат 124, 32га. Приняв этот результат за точное значение площади полигона a, вычислить СКП и предельную погрешности измерения площади планиметром.
Решение
Табл. 3. 2
| № п/п | Результаты измерений P, га | Погрешности измерений
 , га , га
| Δ 2 |
124, 48 
| +0, 16 | 0, 025 | |
| -0, 14 | 0, 020 | ||
| -0, 20 | 0, 040 | ||
| -0, 10 | 0, 010 | ||
| +0, 22 | 0, 048 | ||
| +0, 24 | 0, 058 | ||
| -0, 26 | 0, 068 | ||
| +0, 08 | 0, 006 |
= 0, 275
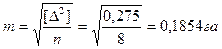 ;
;
 ;
;
 ;
;
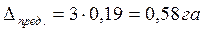 .
.
Задача 1
Для исследования точности измерения горизонтального угла полным приемом теодолитом 3Т5КП, им был многократно измерен угол. Результаты оказались следующими: 39°17, 4′; 39º 16, 8′; 39°16, 6′; 39º 16, 2′; 39°15, 5′; 39°15, 8′; 39°16, 3′; 39°16, 2′. Тот же угол был измерен высокоточным теодолитом 3Т2КП, что дало результат (см. приложение табл. 2). Приняв это значение за точное, вычислить:
|
|
|
– СКП измерений угла;
– определить СКП самого СКП;
– найти предельную погрешность.
3. 3. ОЦЕНКА ТОЧНОСТИ ФУНКЦИИ ИЗМЕРЕННЫХ ВЕЛИЧИН
На содержание этого раздела следует обратить особое внимание и учесть порядок определения СКП функции, вычисляемой по измеренным величинам (аргументам) с СКП, связанными с искомой величиной функционально.
Функция задана в общем виде:
 , (3. 5)
, (3. 5)
где  – аргументы, полученные из измерений с СКП
– аргументы, полученные из измерений с СКП  .
.
СКП функции  вычисляется по формуле:
вычисляется по формуле:
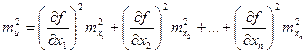 , (3. 6)
, (3. 6)
где 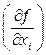 – частные производные функции по каждому аргументу.
– частные производные функции по каждому аргументу.
Порядок вычисления СКП функции общего вида следующий:
1) составляем функцию, связывающую оцениваемую величину с измеренными величинами, например (объем цилиндра):
 ,
,
где  – радиус основания цилиндра;
– радиус основания цилиндра;
 – высота цилиндра.
– высота цилиндра.
Объем цилиндра является функцией двух аргументов – радиуса и высоты, а  – постоянная;
– постоянная;
2) применяя формулу (3. 6), записываем СКП V в общем виде:
 ;
;
3) находим частные производные:
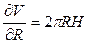 ,
, 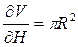 ;
;
4) полученные выражения частных производных подставляем в формулу СКП функции:
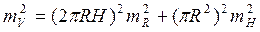 ;
;
5) в соответствии с условием задачи в полученную формулу подставляем числовые значения аргументов и их СКП и вычисляем величину 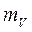 .
.
Решение задач
Пример 3
Пусть проложен висячий теодолитный ход. Горизонтальные углы хода  измерялись независимо друг от друга в одинаковых условиях с СКП
измерялись независимо друг от друга в одинаковых условиях с СКП  . Найти СКП
. Найти СКП 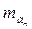 дирекционного угла последней линии рассматриваемого хода. При этом будем считать
дирекционного угла последней линии рассматриваемого хода. При этом будем считать 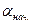 величиной безошибочной.
величиной безошибочной.
Решение
Для определения погрешности дирекционного угла последней линии, прежде всего, необходимо представить этот дирекционный угол как функцию исходных и измеренных величин. Так как были измерены правые по ходу углы, искомый дирекционный угол может быть вычислен по формуле
|
|
|
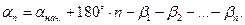
На основании формулы (3. 6) для СКП дирекционного угла последней линии хода можно записать
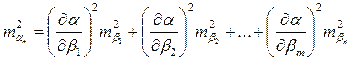 .
.
Получим
 ,
,
или

Окончательно можно сделать вывод, что при передаче дирекционных углов случайные погрешности накапливаются пропорционально корню квадратному из числа измеренных горизонтальных углов.
Пример 4
Для получения горизонтального проложения линии на плане определены координаты концов этой линии, что дало результаты 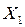 ,
, 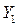 и
и  ,
,  . Эти величины получены со СКП
. Эти величины получены со СКП  и
и 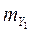 ,
,  и
и  . Необходимо вычислить горизонтальное проложение между этими точками и его СКП.
. Необходимо вычислить горизонтальное проложение между этими точками и его СКП.
|
|
|


