 |
3. 7. Оценка точности измерений углов и превы-
|
|
|
|
3. 7. ОЦЕНКА ТОЧНОСТИ ИЗМЕРЕНИЙ УГЛОВ И ПРЕВЫ-
ШЕНИЙ ПО НЕВЯЗКАМ В ПОЛИГОНАХ И ХОДАХ
Невязки в сумме углов теодолитных полигонов (ходов) являются погрешностями этих сумм, т. е. 
. Поэтому для оценки точности измерений по невязкам используется формула
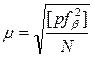, (3. 19)
где 
– невязки;
N – количество невязок;
P – вес отдельного значения невязки.
Если вес вычислять по формуле
; (3. 20)
где n – количество углов хода, то величина СКП единицы веса 
будет равна СКП измерения одного угла
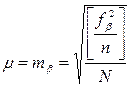. (3. 21)
Для контроля вычисляют 
по другой формуле
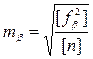. (3. 22)
Невязки в суммах превышений нивелирных полигонов (ходов) являются погрешностями этих сумм. Для вычисления СКП превышения по ходу длиной в 1 км используют формулу
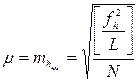, (3. 23)
где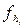 
– невязки, веса которых
(3. 24)
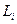– периметры полигонов (ходов) в км.
Контрольная формула
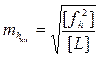. (3. 25)
При значительных углах наклона местности, когда число станций на 1км периметра полигона превышает 25, для вычисления СКП превышения по ходу длиной в 1 км используют формулу
, (3. 26)
где n – число станций (штативов) в полигоне (ходе).
Веса невязок в этом случае вычисляют по формуле
. (3. 27)
Контрольная формула
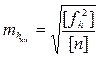. (3. 28)
Решение задач
Пример 12.
Произвести оценку точности нивелирования по невязкам полигонов, указанным в таблице.
| № полигонов | Невязки
 , мм
| Число станций, п |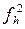 
| 
|
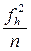
| +32 | ||||
| +2 | 4 | 0 | ||
| -21 | 441 | |||
| + 6 | 36 | 1 | ||
| + 8 | 64 | 2 | ||
| -12 | 144 | 3 | ||
| -31 | 961 | |||
| +15 | 225 | 4 |
|
|
|
[n]=378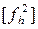 
=2899 
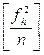= 49
В данном случае СКП единицы веса есть СКП превышения на 1 станцию хода
.
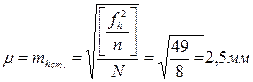Контроль: 
Считая, что в среднем на 1 км хода приходится 10 станций, получим СКП превышения на 1 км по формуле
.
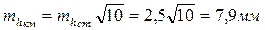Задача 13.
В таблице приведены невязки в полигонах геометрического нивелирования и периметры полигонов. Оценить точность нивелирования.
| № пол-ов | L, км | , мм
|
| +18 | ||
| -14 | ||
| -24 | ||
| +30 | ||
| +34 |
Задача 14.
Произвести оценку точности измерения горизонтальных углов в замкнутом теодолитном ходе (полигоне) по невязкам.
| № полигонов | Число углов в полигонах |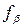 
|
| -2. 5' | ||
| +4, 8 | ||
| -0. 5 | ||
| -2. 8 | ||
| +3. 0 | ||
| +5. 2 |
3. 8. СПРАВОЧНЫЕ СВЕДЕНИЯ
3. 8. 1. ОКРУГЛЕНИЕ ПРИБЛИЖЕННЫХ ЧИСЕЛ
В приближенных вычислениях часто приходиться округлять числа (как приближенные, так и точные), т. е. отбрасывать одну или несколько последних цифр. Чтобы обеспечить наибольшую близость округленного числа к округляемому, соблюдаются следующие правила:
– если первая из отбрасываемых цифр больше или равняется 5, то последняя из сохраняемых цифр усиливается, т. е. увеличивается на единицу;
– если первая из отбрасываемых цифр меньше, чем 5, то усиление не делается;
– если отбрасываемая цифра 5, а за ней нет значащих цифр, то округление производится на ближайшее четное число (правило Гаусса), т. е. последняя цифра остается неизменной, если она четная и усиливается, если – нечетная.
Пример: 15, 458 ≈ 15, 46; 22, 144 ≈ 22, 14; 36, 655 ≈ 36, 66.
3. 8. 2. ТОЧНОСТЬ ПРИБЛИЖЕННЫХ ЧИСЕЛ
Точность приближенных чисел определяется числом значащих цифр. Например: число 28, 3 имеет три значащих цифры. Число 0, 00422 имеет тоже три значащих цифры. Число 1, 06005 имеет шесть значащих цифр. Число 2500, 0 имеет пять значащих цифр, так как оно верно до десятых долей единицы.
|
|
|
Если вместо числа 25643 взять число 26000, то говорят, что в округленном числе имеется две значащие цифры; рекомендуемая запись этого числа – 263103.
3. 8. 3. ПОГРЕШНОСТИ ИЗМЕРЕНИЙ
Точность измерений характеризуется погрешностями измерений. Погрешностью 
измерения называют разность между измеренным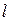 
и ее точным значением a, т. е.
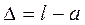. (3. 30)
Погрешность называется абсолютной.
Отношение погрешности к измеренной величине, выраженное дробью, в числителе которой единица, называют относительной погрешностью
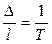. (3. 31)
|
|
|
