 |
Задача 8. Если принять, что измерение отрезка по карте выполняется с той же точностью, что и измерение любой координаты, то приходим к выводу, что получение длины непосредственно с плана будет иметь вес
|
|
|
|
.
Подставляя значения частных производных в формулу обратного веса, получим

Следовательно,
 .
.
Если принять, что измерение отрезка по карте выполняется с той же точностью, что и измерение любой координаты, то приходим к выводу, что получение длины  непосредственно с плана будет иметь вес равный единице, т. е. в два раза больший, чем ее косвенное вычисление через измеренные координаты.
непосредственно с плана будет иметь вес равный единице, т. е. в два раза больший, чем ее косвенное вычисление через измеренные координаты.
.
Задача 8.
Чему равен вес среднеарифметического значения угла, полученного из  =.... приемов (см. приложение табл. 2)?
=.... приемов (см. приложение табл. 2)?
Задача 9.
Определить вес площади прямоугольного треугольника, если катеты: а = 50 м и b = 80 м измерены с весами  ,
, 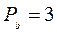 .
.
Задача 10.
Чему равен вес угла, измеренного тремя приемами, если вес угла, измеренного одним приемом, равен 1.
3. 6. МАТЕМАТИЧЕСКАЯ ОБРАБОТКА РЯДА РЕЗУЛЬТАТОВ
НЕРАВНОТОЧНЫХ ИЗМЕРЕНИЙ
При математической обработке неравноточных измерений одной и той же величины решаются последовательно следующие задачи:
1) определяют средневесовое значение из результатов измерений
 , (3. 14)
, (3. 14)
где 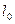 – приближенное (как правило – наименьшее) значение измеряемой величины;
– приближенное (как правило – наименьшее) значение измеряемой величины;
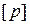 – сумма весов;
– сумма весов;
2) определяют СКП единицы веса по формуле:
 ; (3. 15)
; (3. 15)
3) вычисляют СКП самой СКП единицы веса
 , (3. 16)
, (3. 16)
4) вычисляют СКП средневесового значения
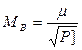 . (3. 17)
. (3. 17)
Для удобства вычислений применяется табличная форма.
В зависимости от условия задачи для различных видов измерений веса можно вычислять по следующим формулам:
 ;
;  ;
;  ;
;  , (3. 18)
, (3. 18)
где 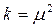 – произвольно выбранное число равное квадрату СКП единицы веса;
– произвольно выбранное число равное квадрату СКП единицы веса;
|
|
|
L – длина нивелирного хода в км;
п – число углов поворота в теодолитном ходе или число станций в нивелирном ходе.
Решение задач
Пример 11.
На заложенный грунтовый репер по четырем ходам геометрического нивелирования различной длины 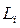 передана высота
передана высота 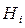 :
:
| № ходов | 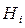 , м , м
| 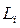 , км , км
|
| 134, 172 | 8, 1 | |
| 211 | 4, 2 | |
| 188 | 5, 3 | |
| 195 | 6, 0 |
Произвести математическую обработку ряда высот.
Решение.
В данной задаче неравноточность высот обусловлена различными длинами нивелирных ходов. Так как, 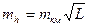 , то вес
, то вес 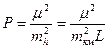 . Обозначив постоянную величину
. Обозначив постоянную величину 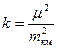 , получим
, получим  , т. е. вес превышения по всему ходу геометрического нивелирования обратно пропорционален длине хода.
, т. е. вес превышения по всему ходу геометрического нивелирования обратно пропорционален длине хода.
| № ходов | Высоты
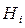 , м , м
| Длина хода
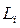 , км , км
| Вес
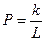

| Остатки
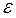 , мм , мм
|  ,
мм ,
мм
| V, мм | 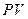 ,
мм ,
мм
| 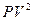
| 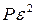
|
| 134, 172 | 8, 1 | 0, 62 | +22 | +13, 6 | |||||
| 4, 2 | 1, 19 | + 39 | + 46, 4 | -17 | -20, 2 | ||||
| 5, 3 | 0, 94 | + 16 | + 15, 1 | +6 | + 5, 7 | ||||
| 6, 0 | 0, 83 | + 23 | + 19, 2 | - 1 | - 0, 8 |

 =3, 58
=3, 58  +80, 7
+80, 7  = -1, 8 678 2494
= -1, 8 678 2494
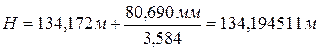 ;
;
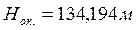 ;
;
Контроль: [PV]=0.
За счет округления величины  появляется ошибка округления
появляется ошибка округления 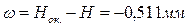 .
.
В этом случае контролем является выражение

 ; [PV] = -0, 511·3, 58 = -1, 8.
; [PV] = -0, 511·3, 58 = -1, 8.
Контроль вычисления  :
:
 .
.  .
.
СКП единицы веса будет равна (СКП превышения, полученного по ходу длиной 5км)
 .
.
СКП самой СКП единицы веса
 .
.
Следовательно,
 .
.
СКП средневесового значения равна
 .
.
Средняя квадратическая погрешность превышения, полученного по ходу длинной в 1км, будет
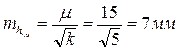 ,
,
что соответствует IV классу геометрического нивелирования. Вес уравненного значения высоты репера равен сумме весов результатов измерений
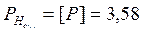 .
.
Ответ: 
Задача 11.
Горизонтальный угол измерен различным числом приемов. Произвести математическую обработку результатов измерений (см. приложение табл. 2).
|
|
|
| № п/п | Значение угла | Количество приемов |
| 54°12'18'' | ||
| 22 | ||
| 20 | …… |
Задача 12.
По четырем теодолитным ходам на узловую линию передан дирекционный угол. Число горизонтальных углов поворота в каждом ходе различно. Произвести математическую обработку результатов значений дирекционных углов узловой линии (см. приложение табл. 2).
| № п/п | Значение дирекционного угла | Число углов в ходах |
| 271º 33, 5' 35, 2 | ........ | |
| 30, 0 | ||
| 32, 8 | . …… |
|
|
|


