Вопросы для самопроверки. ПРИЛОЖЕНИЕ. Варианты индивидуальных заданий для выполнения. контрольной работы 1 - «Тахеометрическая съемка»

Вопросы для самопроверки

1. Какие измерения называют равноточными?

2. Что называется погрешностью измерений?

3. Как классифицируются погрешности измерений?

4. Какими свойствами обладают случайные погрешности?

5. Что называется СКП?

6. Что называется предельной погрешностью измерения?

7. По какой формуле вычисляется СКП линейной функции измеренных величин?

8. По какой формуле вычисляется СКП функции общего вида?

9. Чему равна СКП алгебраической суммы измеренных величин в случае равноточных измерений?

10. Что называется арифметической серединой или среднеарифметическим значением?

11. По какой формуле вычисляется СКП одного измерения, если имеется ряд результатов равноточных измерений одной и той же величины, точное значение которой неизвестно?

12. Во сколько раз СКП арифметической середины меньше СКП одного измерения, имея в виду равноточные измерения одной и той же величины?

13. Какие измерения называются неравноточными?

14. Что называется весом результата измерения?

15. Какими свойствами обладают веса результатов измерений?

16. Что называется СКП единицы веса?

17. Что такое обратный вес?

18. По какой формуле вычисляется обратный вес линейной функции измеренных величин?

19. По какой формуле вычисляется обратный вес функции общего вида?

20. Чему равен вес алгебраической суммы измеренных величин, если вес каждого измерения равен единице?

21. Чему равен вес арифметической середины, если вес каждого измерения равен единице?

22. Что называется общей арифметической серединой или средневесовым значением?

23. Что называют вероятнейшим значением измеряемой величины в случае неравноточных измерений этой величины?

24. Чему равен вес общей арифметической середины?

25. По какой формуле вычисляется СКП единицы веса, если известны погрешности результатов измерений и их веса?

26. По какой формуле вычисляется СКП общей арифметической середины, если известны СКП единицы веса и веса результатов измерений?

27. Что называется математической обработкой результатов неравноточных измерений одной и той же величины?

28. По какой формуле вычисляется СКП измерения угла, если даны невязки в полигонах или ходах?

29. По какой формуле вычисляется СКП нивелирования на 1км хода, если известны невязки в полигонах или ходах?

ПРИЛОЖЕНИЕ

Таблица 1

 

Варианты индивидуальных заданий для выполнения

контрольной работы 1 - «Тахеометрическая съемка»

 

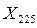№ п/п	º ′	º ′	, м	, м	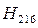, м	, м
	221 11, 0	353 41, 0	+ 4212, 40	- 2380, 84	209, 19	212, 45
	221 16, 5	353 46, 5	4212, 94	- 2380, 90	210, 19	213, 45
	221 21, 0	353 51, 0	4213, 48	- 2380, 96	211, 27	214, 53
	221 26, 5	353 56, 5	4214, 02	- 2381, 02	212, 35	215, 61
	221 31, 0	354 01, 0	4214, 56	- 2381, 08	213, 43	216, 69
	221 36, 5	354 06, 5	4215, 10	- 2381, 14	214, 51	217, 77
	221 41, 0	354 11, 0	4215, 64	- 2381, 20	215, 59	218, 85
	221 46, 5	354 16, 5	4216, 18	- 2381, 26	216, 67	219, 93
	221 51, 0	354 21, 0	4216, 72	- 2381, 32	217, 75	221, 01
	221 56, 5	354 26, 5	4217, 26	- 2381, 38	218, 83	222, 09
	222 01, 0	354 31, 0	4217, 80	- 2381, 44	219, 91	223, 17
	222 06, 5	354 36, 5  4218, 34		- 2381, 50	220, 99	224, 25
	222 11, 0	354 41, 0	4218, 89	- 2381, 54	222, 07	225, 33
	222 16, 5	354 46, 5	4219, 43	- 2381, 59	223, 15	226, 41
	222 21, 0	354 51, 0	4219, 97	- 2381, 64	224, 23	227, 49
	222 26, 5	354 56, 5	4220, 51	- 2381, 69	225, 31	228, 57
	222 31, 0	355 01, 0	4221, 05	- 2381, 74	226, 39	229, 65
	222 36, 5	355 06, 5  4221, 59		- 2381, 79	227, 47	230, 73
	222 41, 0	355 11, 0	4222, 13	- 2381, 84	228, 55	231, 81
	222 46, 5	355 16, 5	4222, 67	- 2381, 89	229, 63	232, 89
	222 51, 0	355 21, 0	4223, 21	- 2381, 94	230, 71	233, 97
	222 56, 5	355 26, 5	4223, 75	- 2381, 99	231, 79	235, 05
	223 01, 0	355 31, 0	4224, 29	- 2382, 04	232, 87	236, 13
	223 06, 5	355 36, 5	4224, 83	- 2382, 09	233, 95	237, 21
	223 11, 0	355 41, 0	4225, 37	- 2382, 14	235, 03	238, 29
	223 16, 5	355 46, 5	4225, 91	- 2382, 19	236, 11	239, 37
	223 21, 0	355 51, 0	4226, 45	- 2382, 24	237, 19	240, 45
	223 26, 5	355 56, 5	4226, 99	- 2382, 29	238, 27	241, 53
	223 31, 0	356 01, 0	4227, 53	- 2382, 34	239, 35	242, 61
	223 36, 5	356 06, 5	4228, 07	- 2382, 39	240, 43	243, 69
	223 41, 0	356 11, 0	4228, 61	- 2382, 44	241, 51	244, 77
	223 46, 5	356 16, 5	4229, 15	- 2382, 49	242, 59	245, 85
	223 51, 0	356 21, 0	4229, 69	- 2382, 54	243, 67	246, 93
	223 56, 5	356 26, 5	4230, 29	- 2382, 59	244, 75	248, 01
	224 01, 0	356 31, 0	4230, 77	- 2382, 64	245, 83	249, 09
	224 06, 5	356 36, 5	4231, 31	- 2382, 69	246, 91	250, 17
	224 11, 0	356 41, 0	4231, 85	- 2382, 74	247, 99	251, 25
	224 16, 5	356 46, 5	4232, 39	- 2382, 79	249, 07	252, 33
	224 21, 0	356 51, 0	4232, 93	- 2382, 84	250, 15	253, 41
	224 26, 5	356 56, 5	4233, 47	- 2382, 89	251, 23	254, 49
	224 31, 0	357 01, 0	4234, 01	- 2382, 94	252, 31	255, 57
	224 36, 5	357 06, 5	4234, 55	- 2382, 99	253, 39	256, 65
	224 41, 0	357 11, 0	4235, 09	- 2383, 04	254, 47	257, 73
	224 46, 5	357 16, 5	4235, 63	- 2383, 09	255, 55	258, 81
	224 51, 0	357 21, 0	4236, 17	- 2383, 14	256, 63	259, 89
	224 56, 5	357 26, 5	4236, 71	- 2383, 19	257, 71	260, 97
	225 01, 0	357 31, 0	4237, 25	- 2383, 24	257, 79	261, 05
	225 06, 5	357 36, 5	4237, 79	- 2383, 29	258, 87	262, 13
	225 11, 0	357 41, 0	4238, 33	- 2383, 34	259, 95	263, 21
	225 16, 5	357 46, 5	4238, 87	- 2383, 39	261, 03	264, 29

 

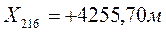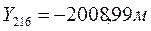, . [1]

 

                                                                                                             Таблица 2

Варианты индивидуальных задач для выполнения

контрольной работы 2- «Теория погрешностей измерений»

 

№ п/п								8
			39º 16'00"		+ 2º 30'		60º 41, 0'		175, 10 м		3		4		10; 15
			16 03		1 45		42, 0		11		4		6		16; 14
			16 06		3 10		43, 0		12		6		2		18; 16
			16 09		3 00		40, 0		13		9		4		16; 18
			16 12		3 30		41, 5		14		6		6		10; 15
			16 15		3 45		42, 5		15		4		2		14; 16
			16 18		4 00		43, 5		16		3		4		16; 18
			16 21		4 12		40, 5		17		4		6		15; 10
			16 24		4 28		41, 0		18		6		2		14; 16
	10		16 27		4 35		42, 0		19		9		4		16; 18
	11		16 30		4 42		43, 0		20		4		6		15; 10
	12		16 33		4 50		40, 0		21		6		2		16; 14
	13		16 36		4 55		41, 5		22		9		4		18; 16
	14		16 39		5 00		42, 5		23		3		6		10; 14
	15		16 42		5 02		43, 5		24		4		2		14; 10
	16		16 45		5 05		40, 5		25		6		4		15; 10
	17		16 48		5 24		41, 0		26		9		6		10; 15
	18		16 51		5 17		42, 0		27		3		2		16; 18
	19		15 48		5 30		43, 0		28		4		4		18; 16
	20		15 51		5 32		40, 0		29		6		6		10; 15
	21		15 54		5 33		41, 5		30		9		2		16; 14
	22		15 57		5 35		42, 5		31		3		4		16; 18
	23		16 01		5 40		43, 5		32		4		6		10; 15
	24		16 04		5 42		40, 5		33		6		2		16; 18
	25		16 05		5 45		41, 0		34		9		4		14; 16
	26		16 10		5 47		42, 0		35		3		6		16; 14
	27		16 15		5 51		43, 0		36		4		2		15; 10
	28		16 20		5 53		40, 0		37		6		4		10; 15
	29		16 25		5 58		41, 5		38		9		6		16; 18
	30		16 28		6 01		42, 5		39		4		4		18; 16
	31		16 03		1 45		42, 0		11		4		6		16; 14
	32		16 06		3 10		43, 0		12		6		2		18; 16
	33		16 09		3 00		40, 0		13		9		4		16; 18
			16 12		3 30		41, 5		14		6		6		10; 15
			16 15		3 45		42, 5		15		4		2		14; 16
			16 18		4 00		43, 5		16		3		4		16; 18
			16 21		4 12		40, 5		17		4		6		15; 10
			16 24		4 28		41, 0		18		6		2		14; 16
	39		16 27		4 35		42, 0		19		9		4		16; 18
	40		16 30		4 42		43, 0		20		4		6		15; 10
	41		16 33		4 50		40, 0		21		6		2		16; 14
	42		16 36		4 55		41, 5		22		9		4		18; 16
	43		16 39		5 00		42, 5		23		3		6		10; 14
	44		16 42		5 02		43, 5		24		4		2		14; 10
	45		16 45		5 05		40, 5		25		6		4		15; 10
	46		16 48		5 24		41, 0		26		9		6		10; 15
	47		16 51		5 17		42, 0		27		3		2		16; 18
	48		15 48		5 30		43, 0		28		4		4		18; 16
	49		15 51		5 32		40, 0		29		6		6		10; 15
	50		15 54		5 33		41, 5		30		9		2		16; 14

 

Данные для решения задач, номера которых не указаны в таблице,

  общие для всех студентов.    

 

ОСНОВНЫЕ ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ

Производная –этопредел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю. Функцию, имеющую конечную производную, называют дифференцируемой. Процесс вычисления производной называется дифференцированием

,

где   – приращение функции на величину .

Частной производной функции нескольких переменных по одной из этих переменных называется производная, взятая по этой переменной при условии, что все остальные переменные временно постоянны. Для функции двух переменных z = f(x, y) частной производной по переменной x называется производная этой функции по x при постоянном y. Обозначается частная производная по x следующим образом:

Аналогично частной производной функции z = f(x, y) по переменной y называется производная этой функции по y при
постоянном x. Обозначения: .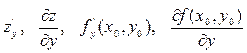

Выполнение заданий предполагает безусловное знание следующих основных правил дифференцирования.

1.  Производная суммы дифференцируемых функций равна сумме производных:

.

2.  Постоянный множитель можно выносить за знак производной:

,

где C – const.

3. Если 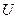 и  - дифференцируемые функции, то существует производная их произведения, которая вычисляется по формуле:

.

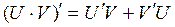4. Если 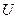 и  - дифференцируемые функции, то существует производная частного, которая вычисляется по формуле:

, .

Для эффективного дифференцирования сложных функций полезна таблица 3. 1. основных элементарных функций, аргумент которых есть тоже функция. Итак, пусть 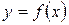, где 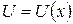. Тогда

1. ,  C – const	2. ,  n – const
3.	4.
5.	6.
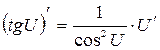
7.	8.
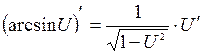
9.	10.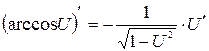
11.	12.
13. 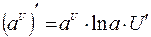, , ,  a – const	14.
15. , , , a – const	16.

   Таблица 3. 1.

⇐ Предыдущая234567891011Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: