 |
Проверка метода эквивалентного генератора
|
|
|
|
2.4.1. Смоделировать электрическую цепь. Вместо численных значений сопротивления исследуемой ветви ввести латинскую букву Т (переменное). Номер ветви взять по указанию преподавателя.
2.4.2. Запустить программу на выполнение в режиме Переходных процессов. В качестве диапазона Т указать 1-25 Ом, в качестве У-параметра указать ток в исследуемой ветви, например 
, если исследуется ветвь 6. Скопировать диаграмму в отчёт.
2.4.3. Изъять из модели сопротивление исследуемой ветви (вытянуть элемент курсором на свободное пространство стола).
2.4.4.. Запустить программу на выполнение в режиме Постоянного тока. Определить значение напряжения между узлами, к которым был подключён изъятый элемент. Принять полученное напряжение за эдс эквивалентного генератора 
(
).
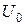2.4.5. Удалить источник эдс из схемы. Образовавшееся пространство замкнуть проводником.
На место удалённого ранее исследуемого сопротивления вставить источник постоянного тока силой 1А.
2.4.6. Запустить программу на выполнение в режиме Постоянного тока. Записать напряжение на источнике тока. Определить значение сопротивления цепи относительно зажимов источника тока. Так как ток источника равен 1А, то сопротивление оставшейся части цепи численно равно напряжению на источнике тока. 
(
). Принять его за сопротивление генератора.
2.4.7. Собрать расчётную схему с эквивалентным генератором. Вместо численных значений сопротивления 
установить латинскую букву Т (переменное).
2.4.8. Запустить программу на выполнение в режиме Переходных процессов. В качестве диапазона Т указать 1-25 Ом, в качестве У-параметра указать ток в исследуемой ветви, например если исследуется ветвь 6. Скопировать диаграмму в отчёт.
|
|
|
Обработка данных
3.1. Проанализировать данные пп. 2.1.4 и 2.1.6. Сделать вывод о справедливости принципа взаимности.
3.2. Проанализировать данные пп. 2.2.2, 2.2.3 и 2.2.4. Сделать вывод о справедливости принципа наложения. По данным п.2.2.2 определить баланс мощностей.
3.3. На основе данных о токах, полученных в п. 2.2.2 рассчитать и построить потенциальную диаграмму внешнего контура. Дать определение диаграммы и пояснения к ней.
3.4. Проанализировать данные п. 2.3.5. Сделать вывод о процессах, происходящих в составном источнике при отсутствии полезной нагрузки.
3.5. Проанализировать графики пп 2.3.2 - 2.3.4. Сделать вывод о процессах, происходящих в составном источнике при разных величинах полезной нагрузки.
3.6. Оценить работу источников при их последовательном соединении (п.2.3.7 и 2.3.8).
3.8. Сопоставить графики по пп. 2.4.2 и 2.4.8. Сделать вывод о справедливости метода эквивалентного генераторав.
Вопросы для самопроверки
1. Что такое «принцип суперпозиции».
2. Что значит «принцип взаимности».
3. Основные этапы расчёта цепей по методу эквивалентного генератора.
4. Когда имеет смысл использовать метод эквивалентного генератора.
5. Как и почему изменяется полезная мощность и кпд источника эдс при изменении полезной нагрузки.
6. Особенности работы параллельно включенных источников разных эдс.
7. Баланс мощностей и его определение.
Лабораторная работа № 2
Исследование линейных цепей переменного тока
Цель работы:
виртуально: исследование цепей с последовательным, параллельным и смешанным соединением элементов;
аналитически: построение векторных и топографических диаграмм, анализ исследуемых цепей.
Основы теории
При изучении теории обратить внимание на следующее.
Переменный синусоидальный ток может быть описан гармонической функцией 
или вектором, вращающимся на комплексной плоскости 
. В последней формуле показана проекция вектора на мнимую ось, j - мнимая единица.
|
|
|
В электротехнике отступают от строгой математической записи уравнения вращающегося вектора. Выражение для тока в символическом виде записывается как 
. В символической форме записи можно вести расчёты как для амплитудных, так и для действующих значений тока.
Аналогично записывают напряжение. Так как начальные фазы напряжения и тока, как правило, не совпадают, то вводят понятия сдвиг фаз 
.
Мгновенное значение мощности в цепях синусоидального тока рассчитывают аналогично расчёту мгновенного значения мощности в цепях постоянного тока
.
Особенность мощности в цепях переменного тока заключена в наличии двух составляющих – постоянной и синусоидальной удвоенной частоты.
На активном элементе мощность также содержит как постоянную, так и синусоидальную составляющие
.
На реактивных элементах мощность содержит только синусоидальную составляющую
, 
.
Для всех линейных элементов цепи справедлив закон Ома в комплексной форме записи: 
, 
, 
. Множители при токе называются, соответственно, активным, индуктивным и ёмкостным сопротивлениями, записанными в комплексном виде. В общем виде комплексное сопротивление записывается единой буквой Z: 
, 
, 
. В цепях с последовательным соединением элементов сопротивления складываются в комплексном виде. Величины, обратные комплексным сопротивлениям, называются соответствующими комплексными проводимостями. В цепях с параллельным соединениям элементов складываются проводимости.
Для цепей переменного тока справедливы законы Кирхгофа в комплексной форме записи 
, 
. Сущностное отличие законов Кирхгофа для цепей постоянного тока от законов Кирхгофа для цепей постоянного тока заключается в том, что для цепей постоянного тока справедливо арифметическое сложение величин, а для цепей переменного тока – геометрическое (векторное) сложение величин.
Комплексная мощность в цепях переменного тока может быть записана одним из двух способовПо формуле 
символически записывается векторная мощность. Векторная мощность изменяется по синусоидальному закону и её можно изображать на диаграммах вращающимися векторами. Для векторной записи мощности справедливы правила векторного сложения мощностей и векторного баланса мощностей. Однако, поскольку частота мощности в два раза превышает частоту тока, на одной векторной диаграмме построение диаграмм мощности и тока (напряжения) не допускается.
|
|
|
По формуле 
, где Р – активная мощность, Q – реактивная символически записываются скалярная мощность. Для скалярной формы записи мощности также справедлив баланс мощностей, но в арифметической форме. Баланс мощностей в цепях переменного тока проверяется по активной и реактивной составляющим.
Для цепи переменного тока на комплексной плоскости можно построить треугольники напряжений, сопротивлений и скалярных мощностей. Все они подобны друг другу, так как определяются общим сдвигом фаз напряжения и тока в цепи.
Для наглядного изображения полученных величин тока и напряжения используют векторные и топографические векторные диаграммы на комплексной плоскости. Векторная диаграмма строится из начала координат и показывает только величину и фазу исследуемой величины. Топографическая векторная диаграмма это векторная диаграмма цепи, построенная с учётом топологии цепи. Здесь каждому узлу цепи соответствует своя точка на топографической диаграмме, а вектору между узлами – падение напряжения на элементе, соединяющем узлы.
Виртуальные исследования
|
|
|
